こんにちは，ハヤシライスBLOGです！
今回は電気回路の重ね合わせの理とテブナンの等価回路について，できるだけ分かりやすく解説します！
テブナンの定理は非常に重要な公式ですが，その成り立ちは重ね合わせの理にあります！重要なのは，テブナンの定理の公式を丸暗記することではなく，その成り立ちをしっかり勉強することで，重ね合わせの理についての理解も深めることです！それではよろしくお願いいたしますI
重ね合わせの理
重ね合わせの理とは，「電源が複数ある回路の電圧・電流は，各電源を一つだけ活かした場合の電圧・電流の足し合わせで求まる」というものです！
例えば，図1のように電源が複数ある回路において，抵抗Rを流れる電流Iを求めたいとしましょう！この場合，重ね合わせの理を使うことで，3つの電圧源があった回路は，図2のようにそれぞれの電圧源を一つだけ活かした3つの回路に分解することができ，抵抗Rを流れる電流Iは，分解した3つの回路の電流I1からI3の和によって求めることができます！勿論，キルヒホッフの法則でもこの回路を解くことはできますが，重ね合わせの理を使うことで，より簡単に計算することができます(^^)/
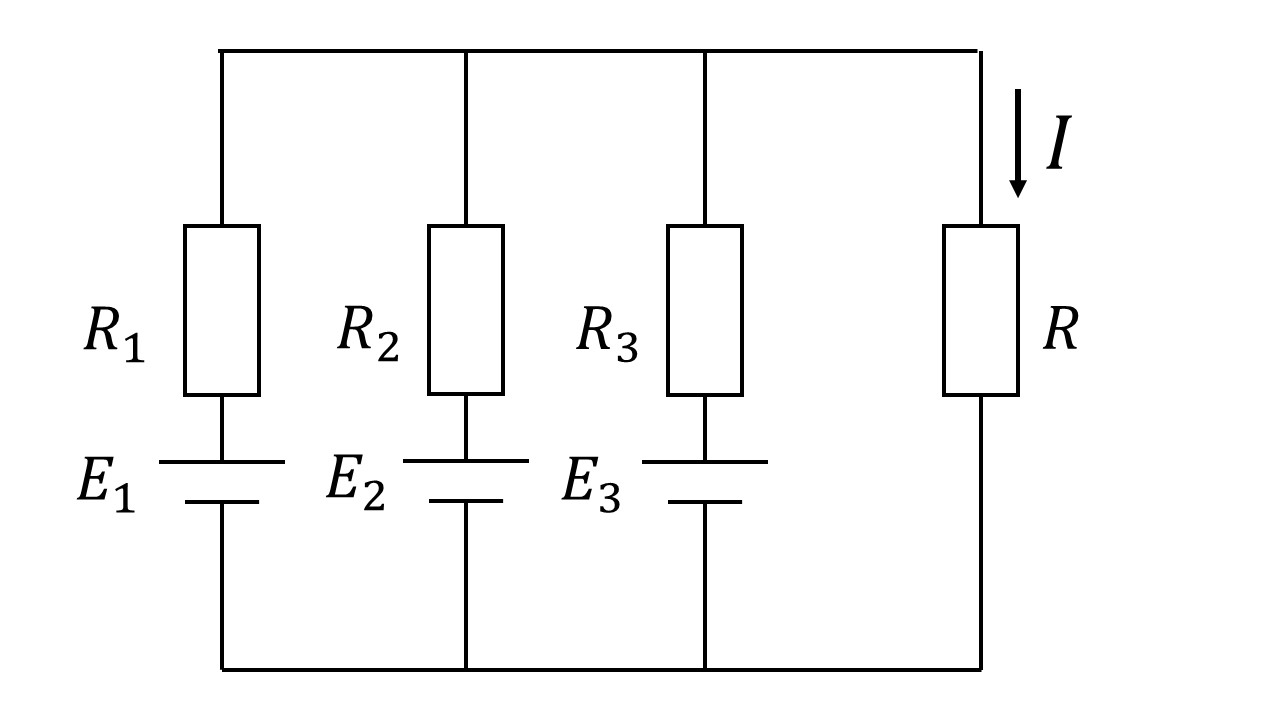図1 電源が複数ある回路の例
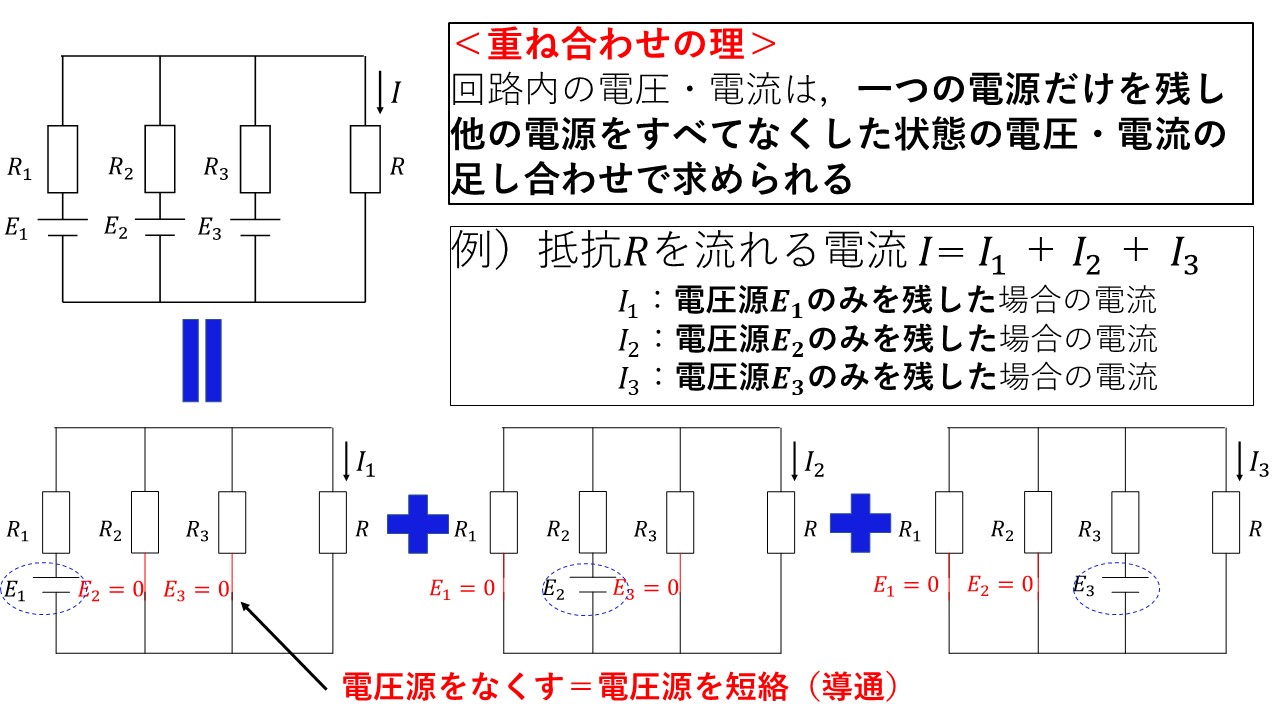図2 重ね合わせの理
このように計算に便利な重ね合わせの理ですが，電源をなくす場合には注意点があります！それは，図3のように電圧源の場合は短絡，電流源の場合は開放することです！しっかりとおさえておきましょう！
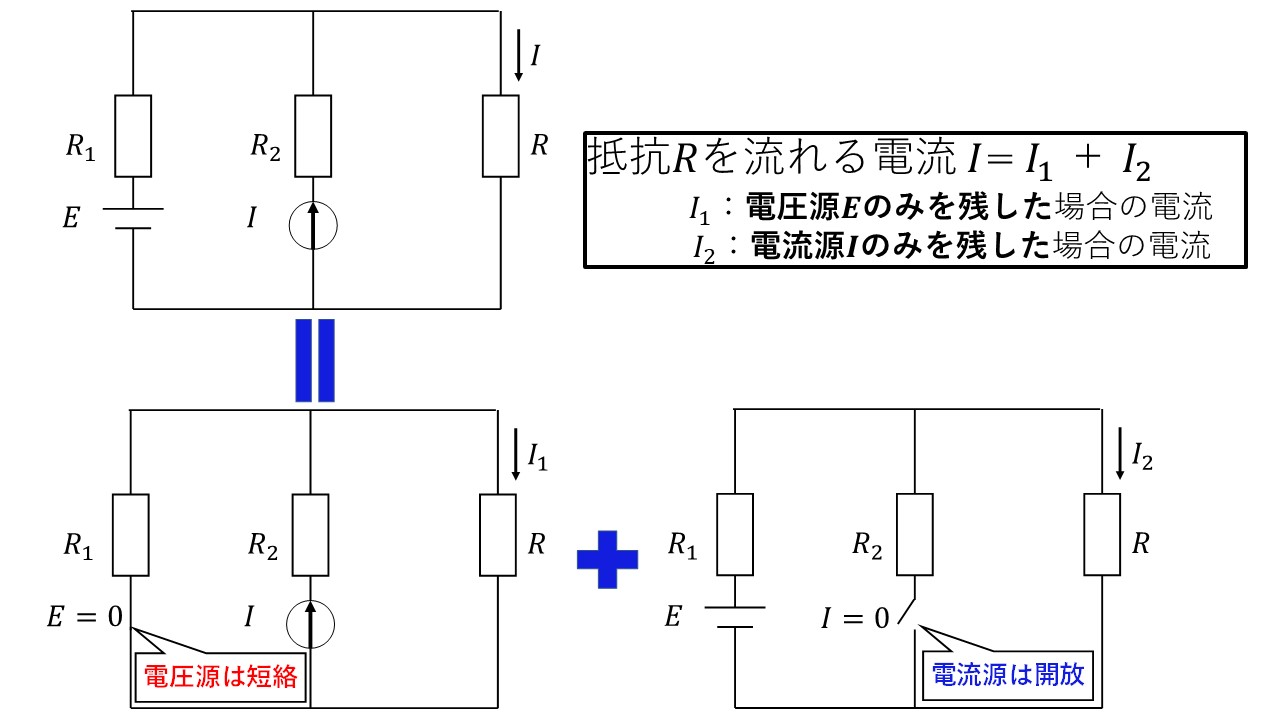
図3 重ね合わせの理を使う際の電圧源と電流源のなくし方
テブナンの定理
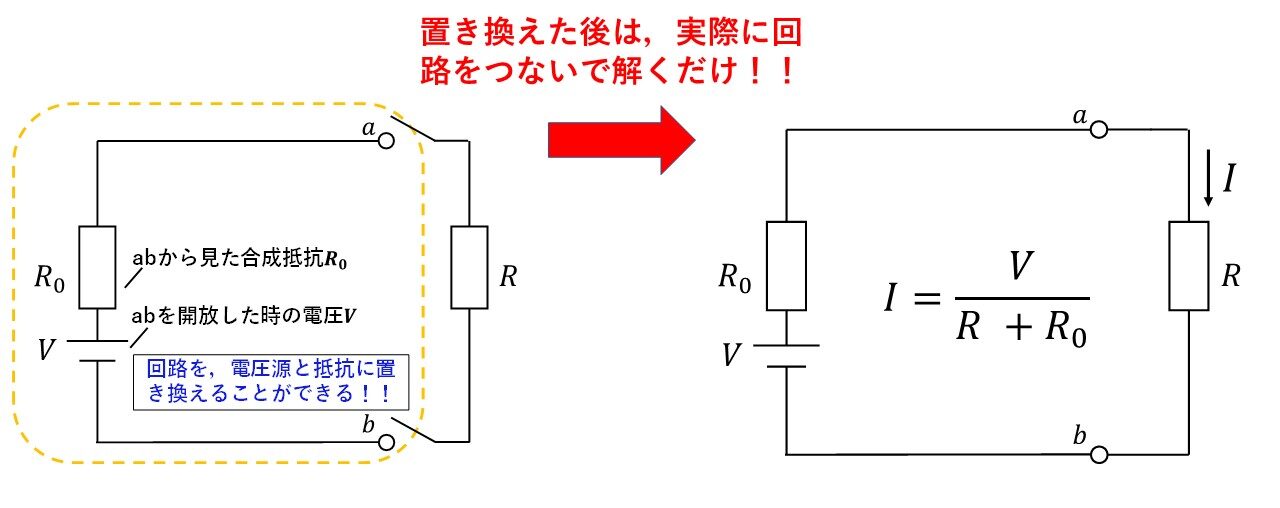
テブナンの定理とは，図4の通り，①ある端子（図4ではab）を開放した（切り離した）場合の電圧Vと，②その端子から見た合成抵抗R0が分かれば，どんな複雑な回路であっても，たった一つの電圧源（開放電圧V）と抵抗R0の簡単な回路に置き換えることができるというものです！
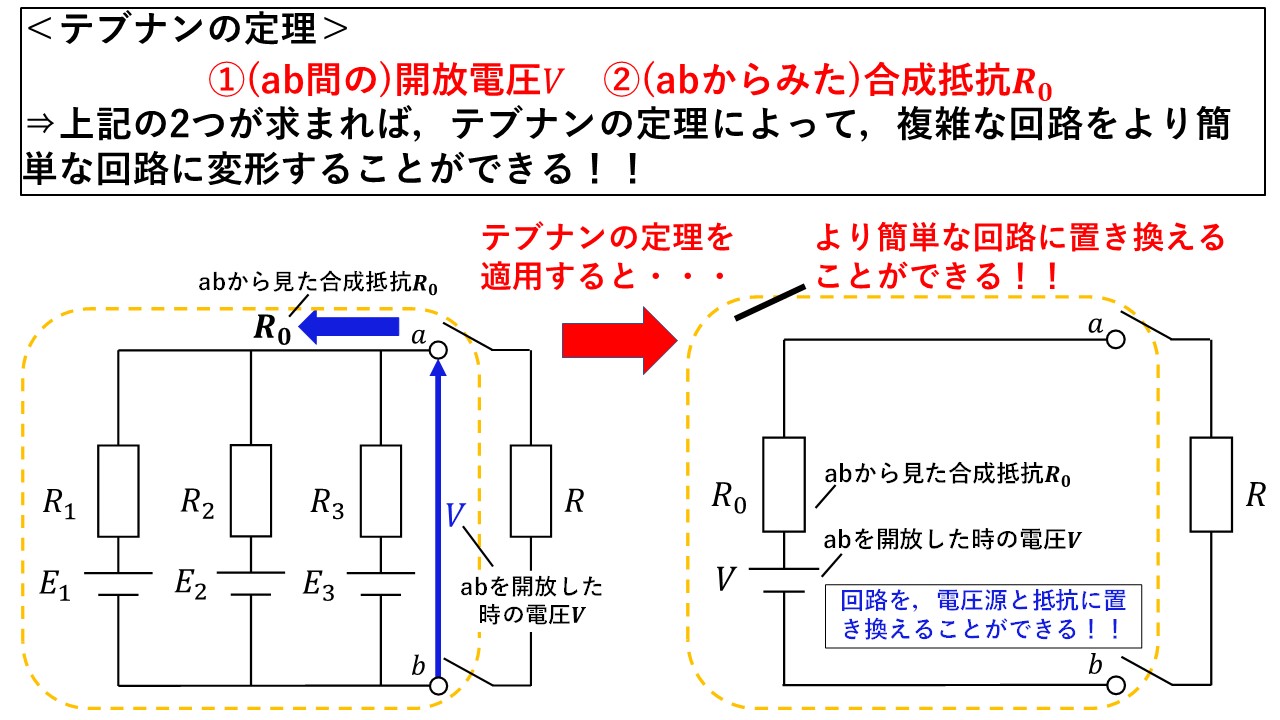
図4 テブナンの定理の概要
置き換えた後は，切り離す前の回路につないで，普段と同じように解くことができます！テブナンの定理によって簡単な回路に置き換えることができたので，抵抗Rを流れる電流はI=V/(R+R0)のように簡単に求めることができます(^^)/
テブナンの定理の成り立ちを知ろう！
このように計算に非常に便利なテブナンの定理ですが，実は重ね合わせの理を応用することで，この定理を導くことができます！以下で，図1の回路を例に説明しますので，しっかりとおさえておきましょう！
Step１：＋Vと－Vの電圧源を足してみよう！
まず図5の左の回路の求めたい電流がある場所に，abを開放した時の電圧Vの大きさを持つ電源を2つ，それぞれ逆向きに追加しましょう！なぜこんな意味の分からないことをやるかはさておき，正負逆向きの電圧源を追加しても，互いに打ち消しあいトータル0になるので，回路的には何も変わらないことを理解しましょう！
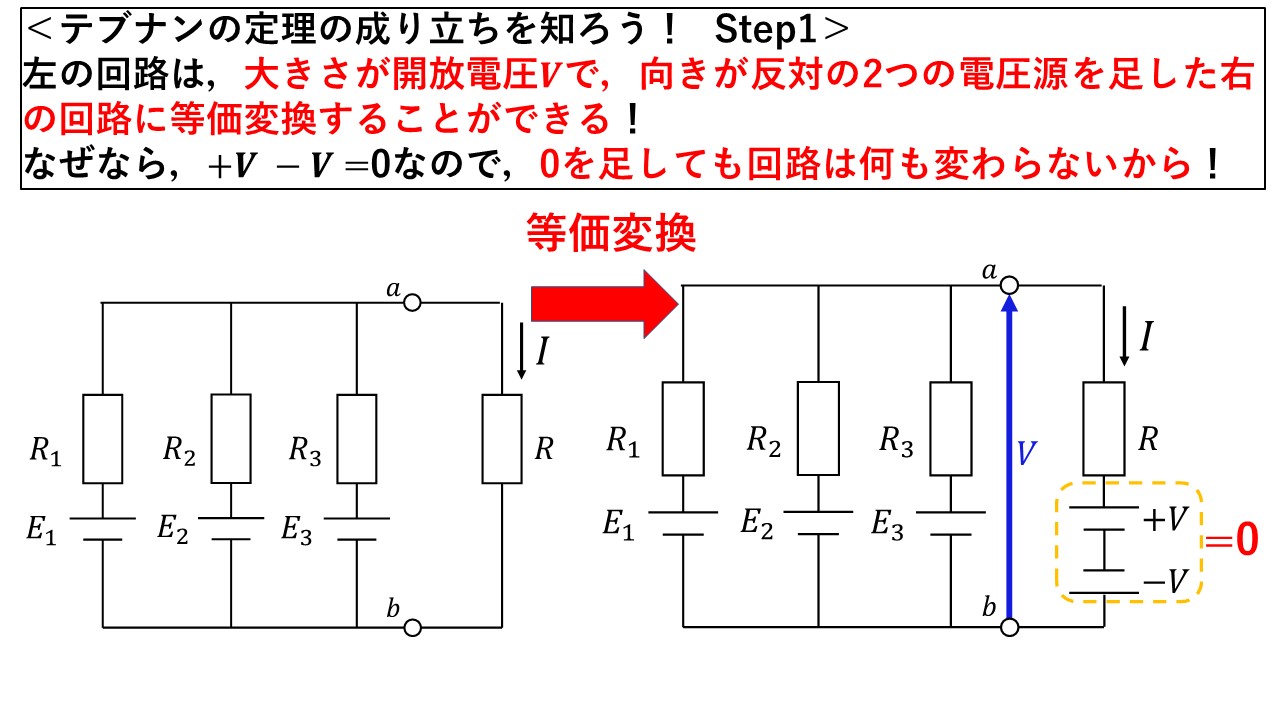図5 Step1：開放電圧Vの電源2つを，正負逆向きに追加しよう！
Step２（の準備）：重ね合わせの理の応用
次にStep2に入る前に，重ね合わせの理の応用編を少しだけ抑えておきましょう！図6にある通り，実は重ね合わせの理とは，必ずしも電源が1つの回路に分解する必要はなくて，電源を複数持つグループに分けて解くこともできます！
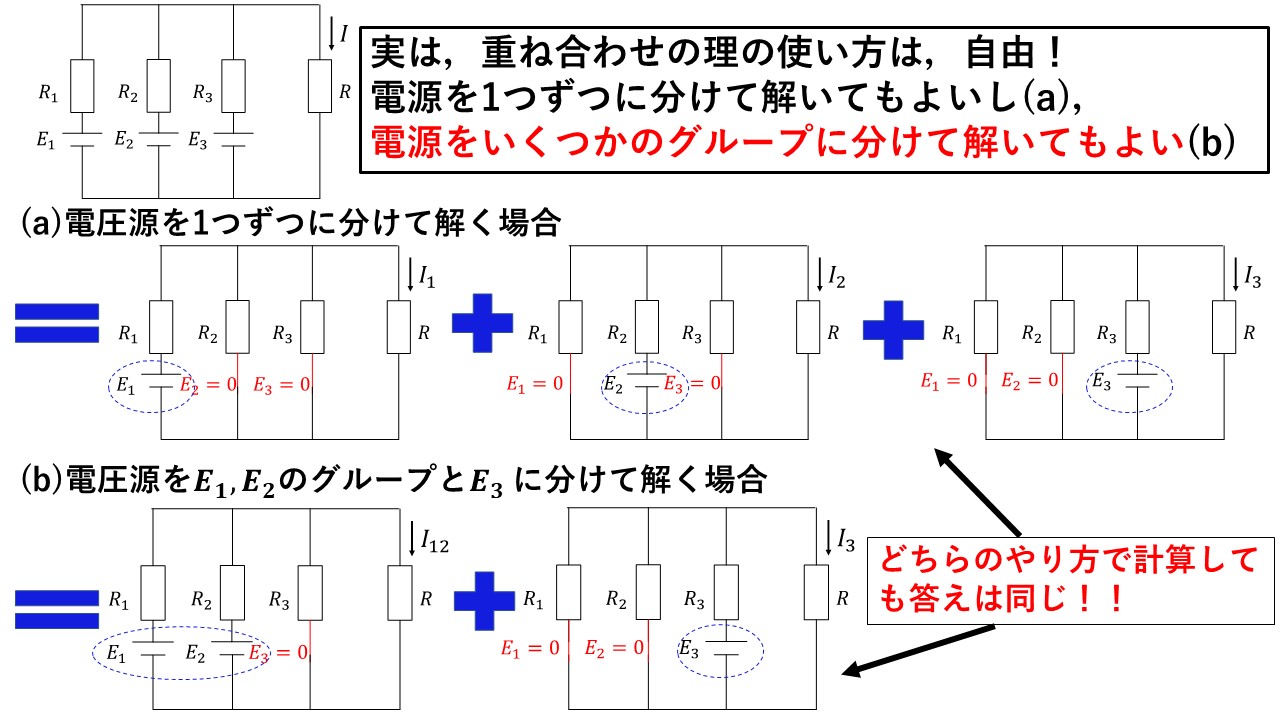図6 Step2（準備）：重ね合わせの理の使い方は自由！
(a)のように電源が1つだけある3つの回路に分解して解いてもよいですし，(b)のように電源を2つ持ったグループと1つしかないグループに分けて解いてもよいです！
結局，(b)の電源を2つ持ったグループも，重ね合わせの理を再び使えば，電源が1つだけある2つの回路に分解できますから，結局(a)とまったく同じになり，答えが変わらないことが理解できますね(^^)/
Step２：2つのグループ（A、B）に分けよう(^^)/
では実際にStep2に入りましょう！Step2の準備で説明したように，重ね合わせの理は電源を複数持つグループに分けて解くことができますから，ここでは－V以外の電源を持つグループAと，－Vの電源のみを持つグループBに分けてみましょう！勿論，求めたい抵抗Rを流れる電流Iは，重ね合わせの理によって「グループAの抵抗Rを流れる電流I1＋グループBの抵抗Rを流れる電流I2」によって計算することができます(^^)/
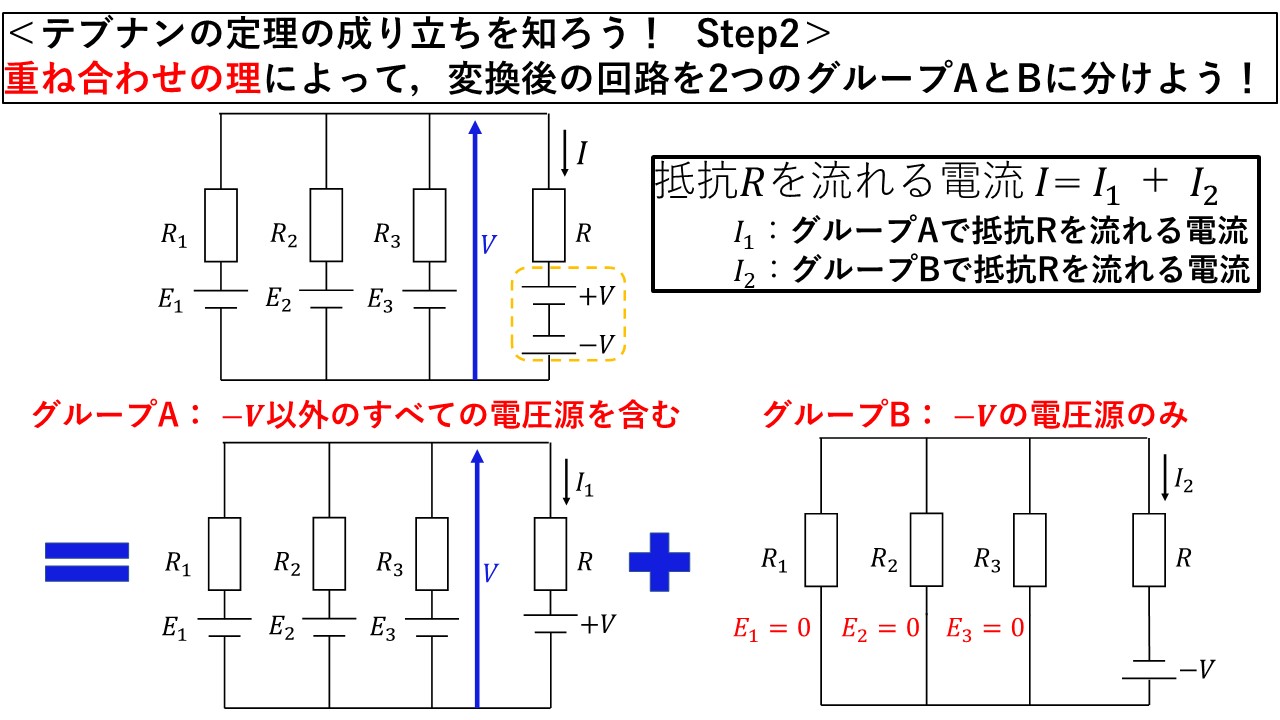図7 Step2：回路を2つのグループに分けてみよう！
Step３：グループA（－V以外の電圧源）の電流を求めよう！
Step3ではグループAの電流を求めてみましょう！抵抗Rを流れる電流は，抵抗両端の電位差÷抵抗で求められます！ここで，抵抗両端の電位差を計算すると・・・，そうなんです0なんです！直流電源の大きさが開放電圧Vと同じ大きさであるため，抵抗両端の電位差は0となり，グループAでは抵抗Rに電流は流れないんです！
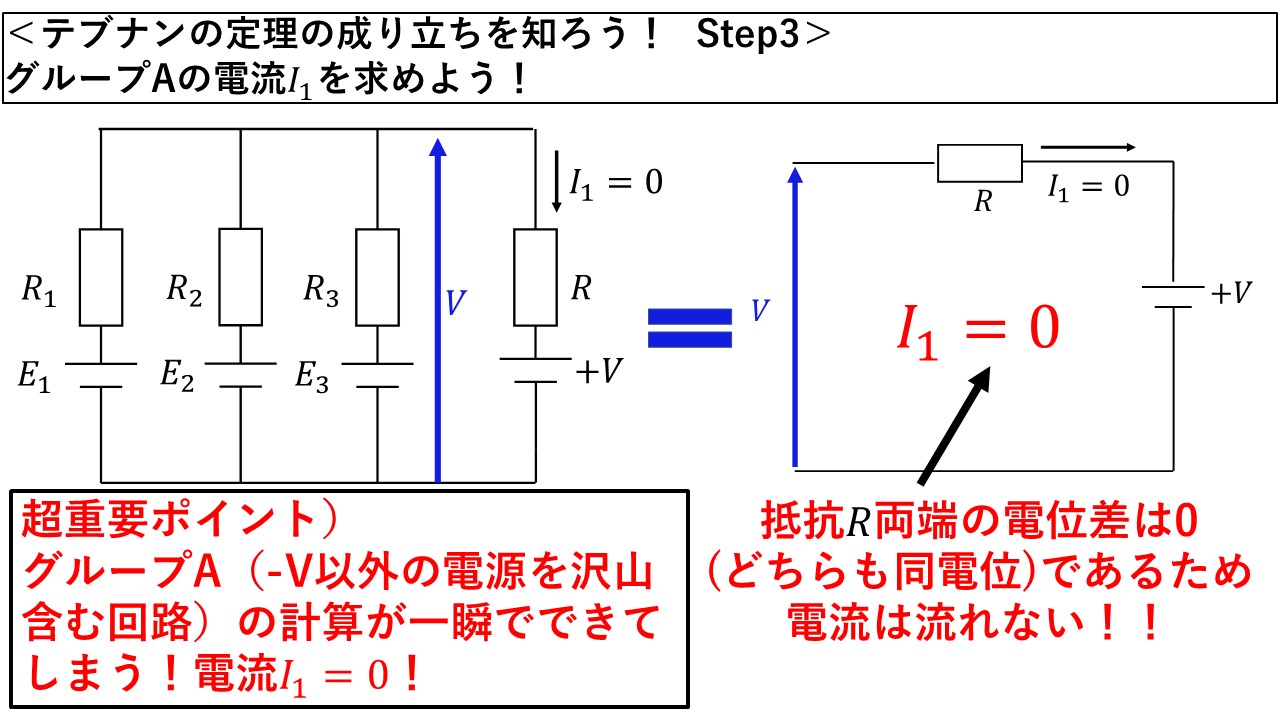図8 Step3：グループAの電流を計算してみよう！
つまり，グループAには沢山の電源が含まれており，本来であればこれらの電源を含んだ状態での回路計算は非常に大変なのですが，開放電圧Vと同じ大きさの直流電源を設定したおかげで，抵抗Rを流れる電流がわずらわしい計算が一切必要なく，I1=0と求まります(^^)/
言い方を変えると，重ね合わせの理によって「元々の回路でRを流れる電流＝グループAでRを流れる電流＋グループBでRを流れる電流」によって求まりますが，大半の電源を含んだグループAの電流は一瞬で0と求まるので，元々の回路の電流は，電源が-Vの直流電源しかないグループBの電流によって決まってしまうということです！めちゃめちゃ計算が楽になりますね(^^)/
このStep3はテブナンの定理の成り立ちを理解する上で，超重要ポイントになりますので，しっかりとおさえておきましょう(^^)/
Step４：グループB（－Vの電圧源）の電流を求めよう！
続いて，Step4ではグループBの電流を求めましょう！グループBでは，-Vの電源しかありませんので，R1からR3の合成抵抗R0を求めれば，グループBの回路は図9の右側の回路と同じになります！なお，この回路は，少し見方を変えると（電圧源の位置を左側に持ってくると），図4と全く同じ回路になっています！
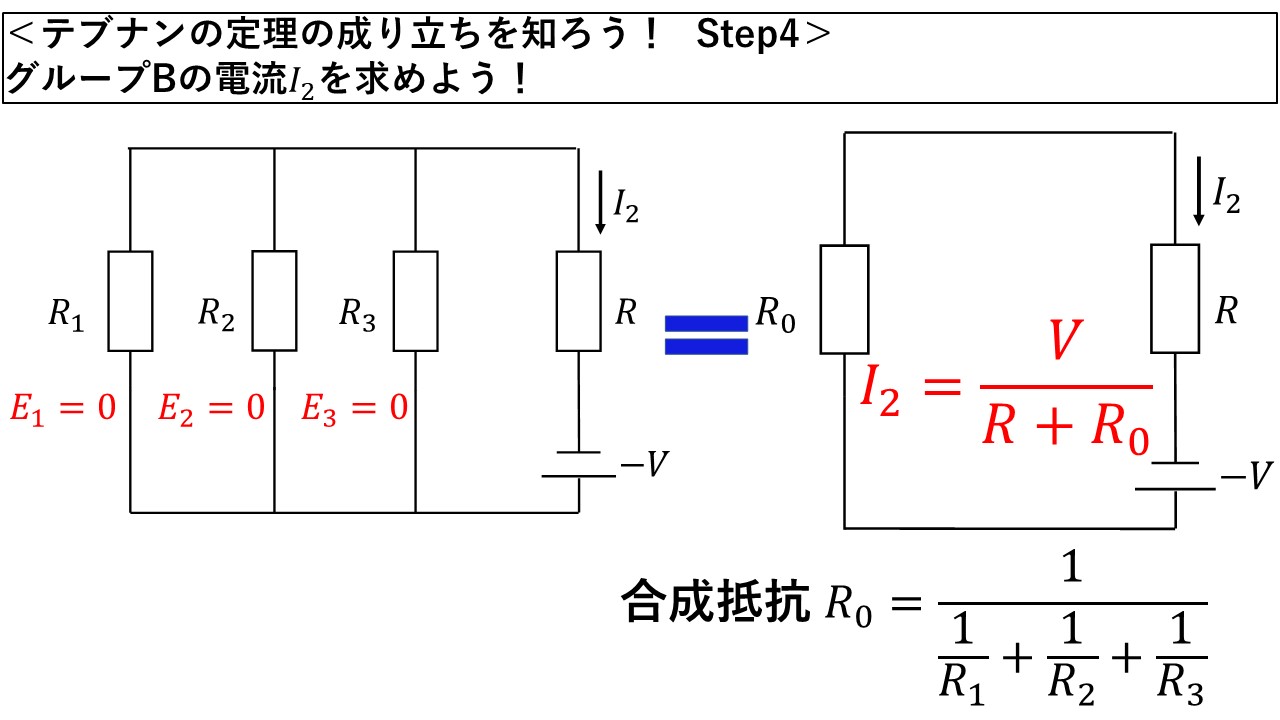図9 Step4：グループBの電流を計算してみよう！
Step5：グループAの電流とグループBの電流を足して，元回路の電流を求めよう！
最後にStep5です！元々の回路で抵抗Rを流れる電流は，重ね合わせの理によって「元々の回路の電流＝グループAの電流＋グループBの電流」によって求まり，グループAの電流は0になりますから，元々の回路で抵抗Rを流れる電流はグループBで求まる電流，すなわち，I=V/(R+R0)と求めることができます！この結果は，図4で述べたテブナンの定理そのものなので，これでテブナンの定理を導出することができましたね！
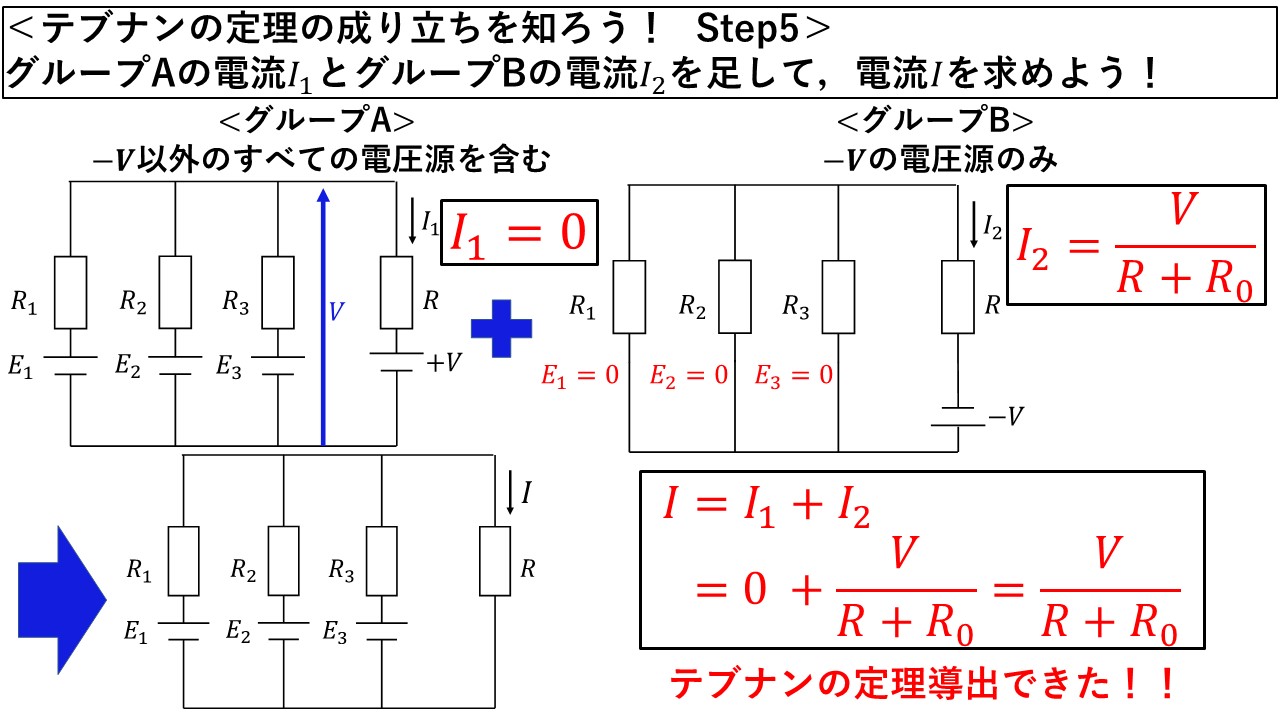
図10 Step5：グループAとグループBの電流を足そう！
テブナンの定理は非常に重要な公式ですが，その成り立ちは重ね合わせの理にあります！あくまでテブナンの定理は，重ね合わせの理を上手く使って導出された公式に過ぎません！重要なのは，重ね合わせの理を理解し，使いこなすことです！テブナンの定理の公式を丸暗記するのではなく，成り立ちをしっかり勉強し，重ね合わせの理の理解も深めましょう(^^)/
（参考）RL回路やRC回路の解き方について分かりやすく解説！
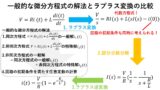
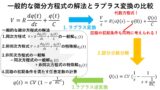
以下の記事では，RL回路やRC回路の解き方について，微分方程式の解法を用いた解き方と，ラプラス変換による解き方の2つの方法を解説しています！興味がある方は是非読んでみてください(^^)/
（参考）電気回路や電験（理論）を0から勉強したい方にオススメの書籍
今回の記事では，テブナンの定理や重ね合わせの理を中心に解説していますが，実際に電験3種の試験や大学の講義の試験の問題を解くには，もっと幅広い知識が必要になります！以下の書籍は，沢山のイラストを用いて，電気回路を0から丁寧に説明しており，初学者の方にとってもオススメの本です！テブナンの定理は勿論，コンデンサ・コイルの性質やそれらを組み合わせた場合の回路の解き方，三相交流の基礎など，幅広い分野を丁寧に解説しており，付録の問題集では，電験3種の過去問が単元毎に整理されているので，理解度を確認するのに非常に便利です！著者も愛用していますので，是非読んでみてください(^^)/
今回の記事はここまでです！この記事が皆さんの役に少しでも立っていると嬉しいです(^^)/
