こんにちは，ハヤシライスBLOGです！今回は基本的な伝達関数のブロックについて，そのステップ応答やボード線図について分かりやすく解説します(^^)/ これらのブロックの特性を忘れてしまった時などに，参考にしてもらえると嬉しいです(^^)/
微分要素
図1が微分要素の伝達関数になります！おさらいですが，sはs=d/dtを意味します！
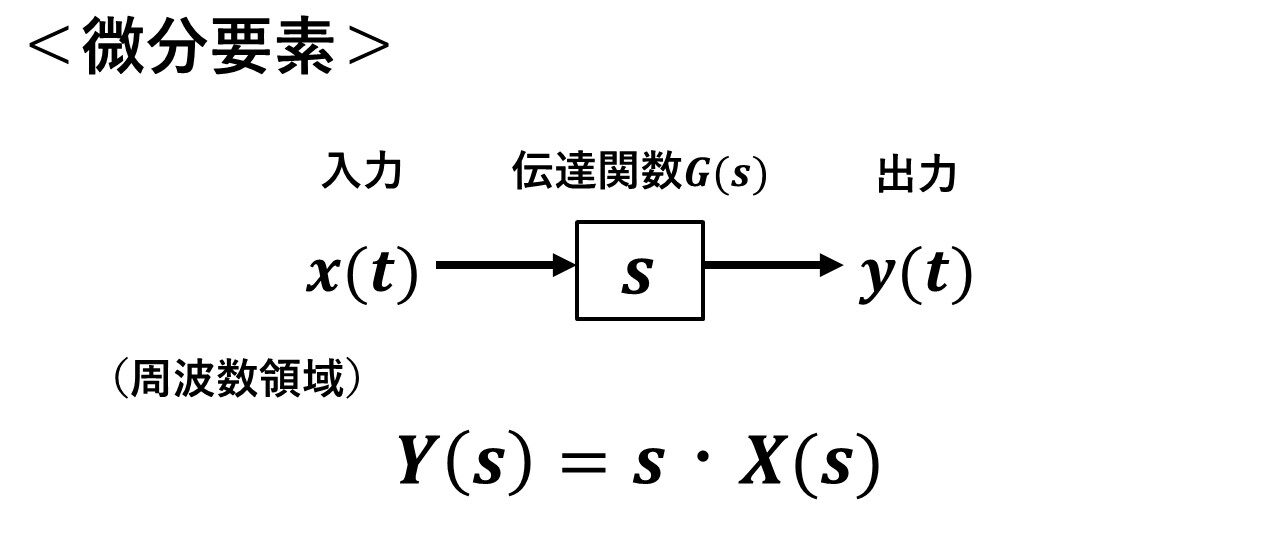図1 微分要素の伝達関数
微分要素の単位ステップ応答
実際に，微分ブロックに単位ステップ信号u(t)（つまり，大きさ1の階段状の信号）を入力した場合の応答を見てみましょう！微分ブロックの単位ステップ応答の計算方法は以下の通りです！一度周波数領域，つまりラプラス変換により出力Y(s)を計算し，最後に逆ラプラス変換で出力y(t)を計算します！
図2 微分ブロックの単位ステップ応答の計算方法
微分ブロックの単位ステップ応答を図3に示します！図2の計算結果の通り，微分ブロックの単位ステップ応答は，単位インパルス信号δ（ｔ）になりますので，ステップ信号が入力された時だけ非常に大きな値となって，それ以外の時間は0になります(^^)/
微分ブロックは，d/dt，つまり，入力の微分（傾き）をとるため，ステップ信号が入力された瞬間は入力信号が0から1に急激に変化するので傾きが∞になり，それ以外の時刻では入力信号は大きさ1で一定，つまり傾き＝0になるので，このような波形になります(^^)/
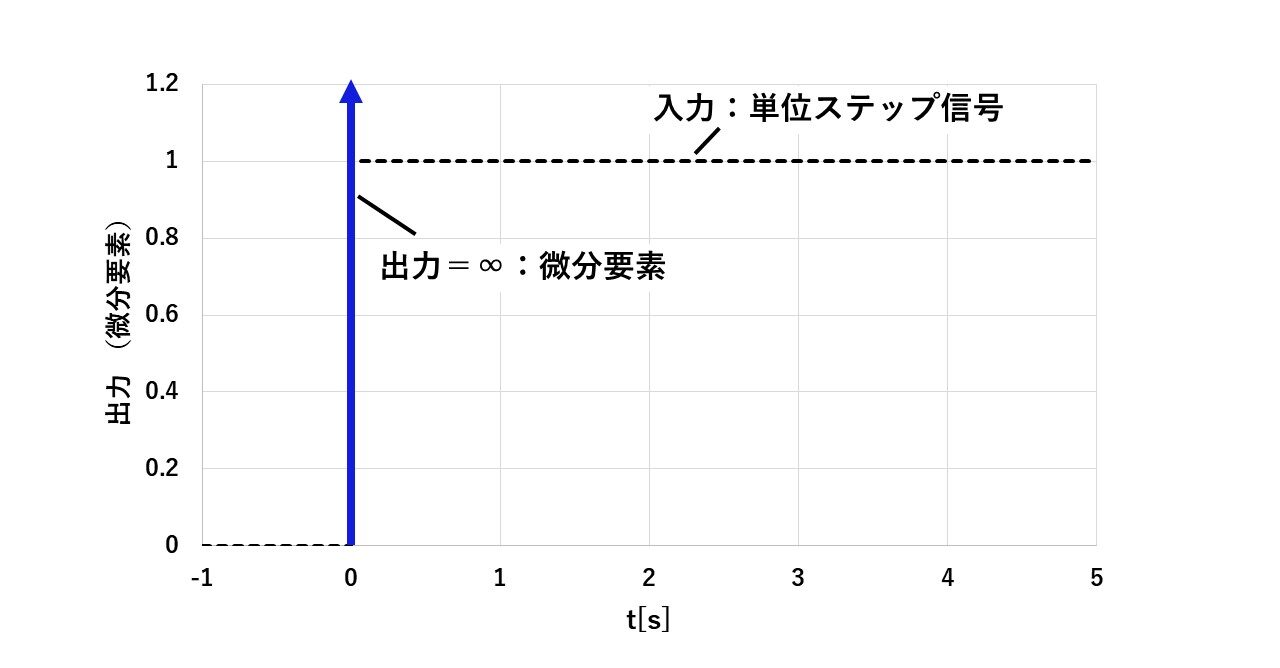図3 微分ブロックの単位ステップ応答
（参考）ラプラス変換，周波数伝達関数，ボード線図について，分かりやすく解説！！
以下の記事では，ラプラス変換や周波数伝達関数，ボード線図について分かりやすく解説しています！どれも無料で読めるので，是非読んでみてください(^^)/
微分要素のボード線図
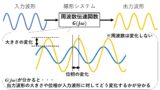
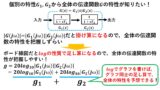
次に微分ブロックのボード線図を求めてみましょう！微分ブロックのボード線図は，図4のように求めることができます！ゲイン特性の縦軸は20log10|G(jω)|でdB表示になっていることに注意しましょう(^^)/
図4 微分ブロックのボード線図の計算方法
図5が，微分ブロックのボード線図になります！同図のワンポイントに書いたように，微分ブロックでは横軸のωが10倍される毎に，縦軸の値が+20[dB]されることに注意しましょう！
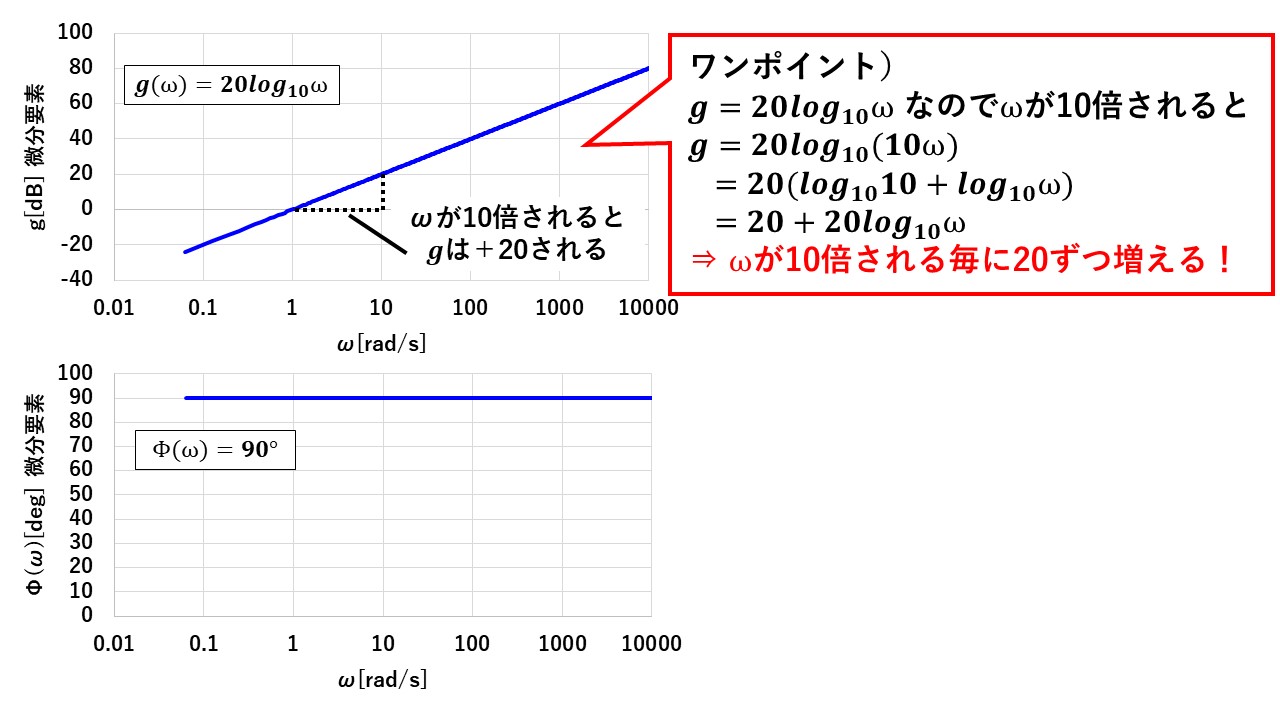図5 微分ブロックのボード線図
積分要素
図6が積分要素の伝達関数になります！おさらいですが，1/sは1/s=∫dtを意味します！
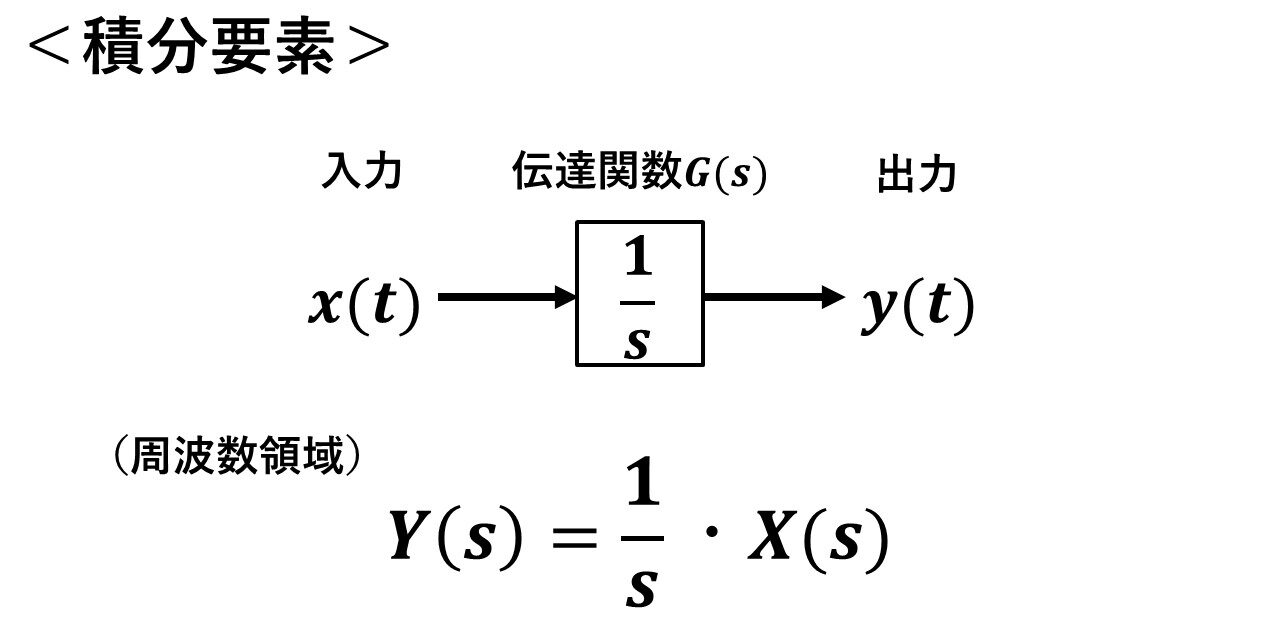図6 積分要素の伝達関数
積分要素の単位ステップ応答
実際に，積分ブロックに単位ステップ信号u(t)を入力した場合の応答を見てみましょう！積分ブロックの単位ステップ応答の計算方法は以下の通りです！
図7 積分ブロックの単位ステップ応答の計算方法
積分ブロックの単位ステップ応答を図8に示します！図7の計算結果の通り，積分ブロックの単位ステップ応答は，y(t)=tになります(^^)/
図8にある通り，積分ブロックは，∫dt，つまり，ある時刻tの積分ブロックの出力は，その時刻までの入力信号の面積になります！そのため，ステップ信号のように大きさ一定の信号を入力した場合，時間が経つごとに入力信号の面積も一定の大きさで増えていくため，積分ブロックの出力がy(t)=tのように傾きが一定で増加していきます(^^)/ このように，単にラプラス変換や逆ラプラス変換によりステップ応答を計算するだけでなく，そのブロックの持つ意味に当てはめて考えるようにすると，より定着しますね(^^)/
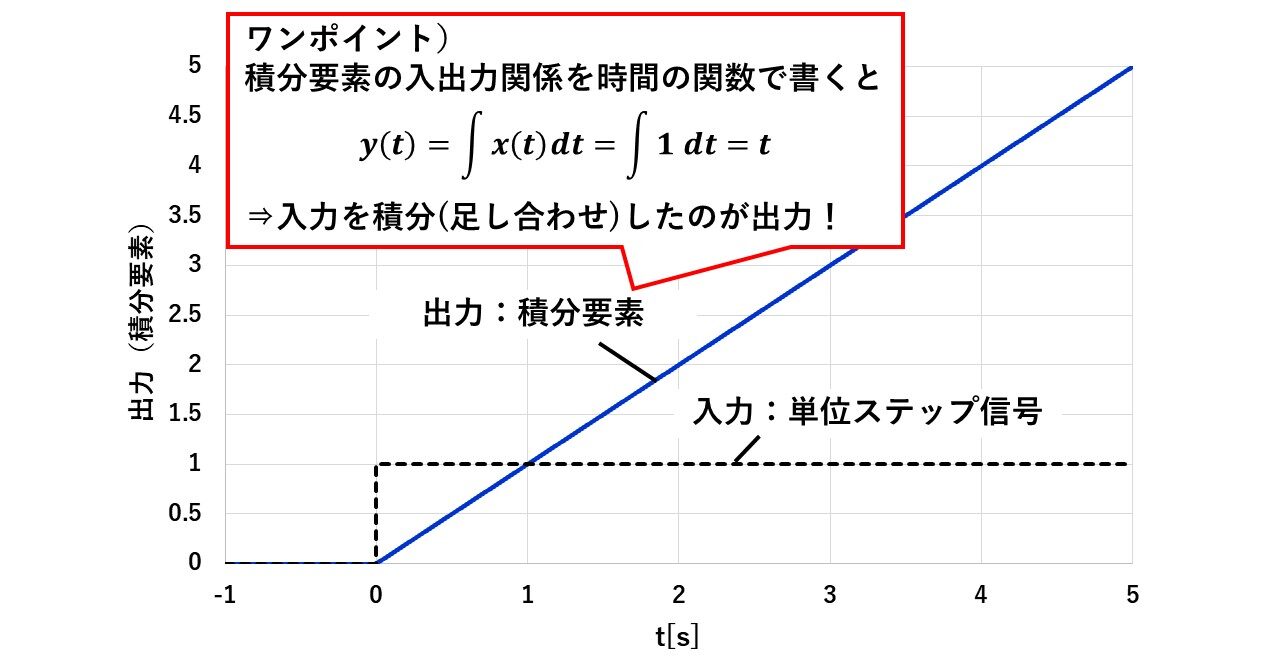図8 積分ブロックの単位ステップ応答
積分要素のボード線図
次に積分ブロックのボード線図を求めてみましょう！積分ブロックのボード線図は，図9のように求めることができます！
図9 積分ブロックのボード線図の計算方法
図10が，積分ブロックのボード線図になります！積分ブロックでは横軸のωが10倍される毎に，縦軸の値が-20[dB]されることに注意しましょう！
図10 積分ブロックのボード線図
（ちょっと休憩）理系大学生が学生時代に必ずやっておくべき5つのこと！！
大学生の皆さん！勉強お疲れ様です(>_<) 以下の記事は，私が理系の大学生の皆さんに向けて，社会人になる前にやっておいた方がよいことを5つに厳選して書いた記事です！これらは，私が社会人になって，「学生時代にこれをやっておいて本当に良かった！」と心から思うことや，「学生時代に何でこれをやっておかなかったんだろうか・・・」と超絶後悔していることなどを厳選しています(^^)/勉強の休憩がてらに，是非見てみてください！
一次遅れ
図11が一次遅れの伝達関数になります！
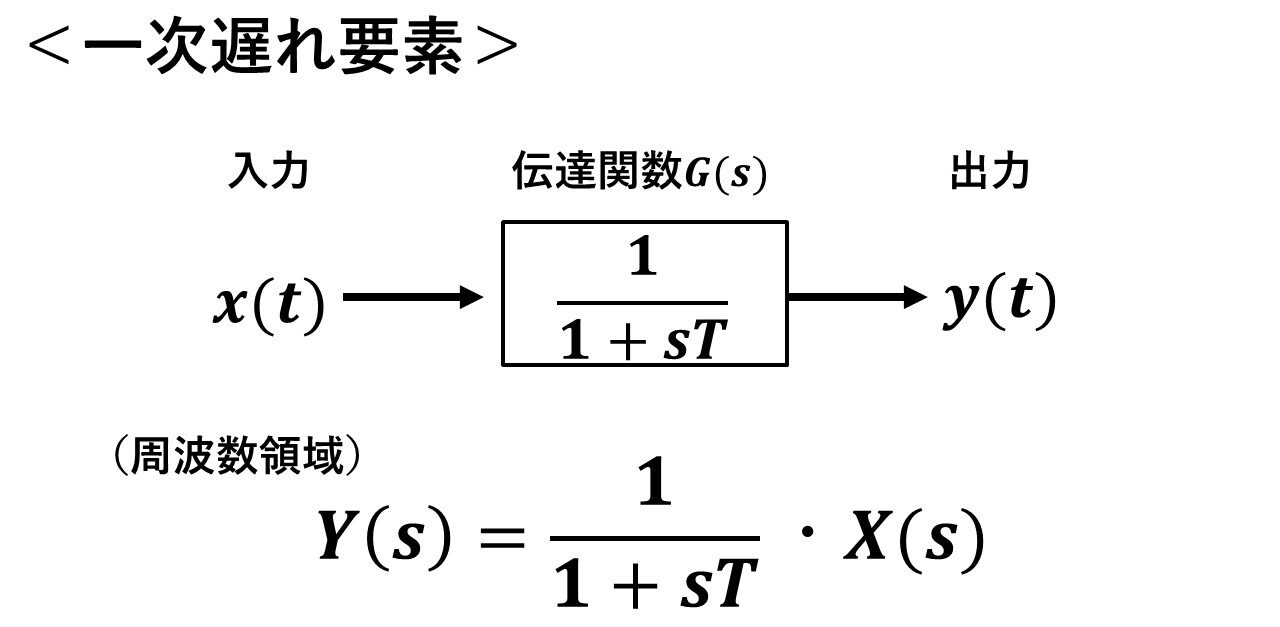図11 一次遅れの伝達関数
一次遅れの単位ステップ応答
一次遅れに単位ステップ信号u(t)を入力した場合の応答を見てみましょう！一次遅れの単位ステップ応答の計算方法は以下の通りです！
図12 一次遅れの単位ステップ応答の計算方法
一次遅れの単位ステップ応答を図13に示します！
図13にある通り，出力が最終値の約63%に到達する時刻を，時定数と呼びます！この例では，時定数を0.1[s]に設定しているので，ステップ信号が入力されてから0.1[s]後に，最終値の約63%に到達しているのが分かります！この時定数が何秒であるかによって制御ブロックの応答がかなり変わりますので，時定数は制御ブロックの特性を把握する上で非常に重要になります！しっかりと押さえておきましょう(^^)/
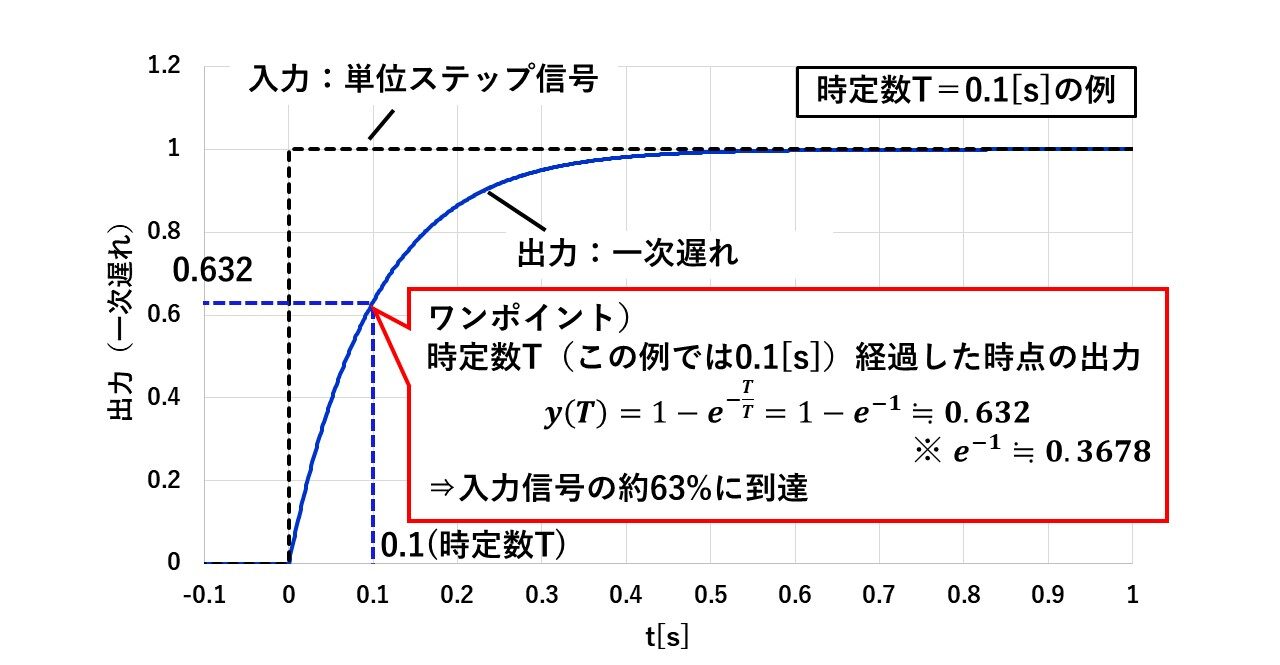図13 一次遅れの単位ステップ応答
一次遅れのボード線図
次に一次遅れのボード線図を求めてみましょう！一次遅れのボード線図は，図14のように求めることができます！
図14 一次遅れのボード線図の計算方法
図15が，一次遅れのボード線図になります！同図のゲイン特性や位相特性を見ると分かる通り，一次遅れのボード線図ではωTの大小関係によってゲイン特性や位相特性が変わり，ω=1/Tの点を境に特性が大きく変化しているのが分かります！このように特性がある周波数を境に大きく変化する周波数を，折点周波数と呼びます！図15のワンポイントにある通り，ωTの大小関係によって，ゲイン特性や位相特性がどのように近似できるかは非常に重要になりますので，しっかりと押さえておきましょう(^^)/
また，一次遅れの場合，ゲイン特性から分かる通り，ω=1/Tより高い周波数成分については縦軸のdB値が小さくなっており，これらの成分は一次遅れの出力では大きく減衰することが分かります！要するに，一次遅れブロックは，ω=1/Tより低い周波数成分を中心に通過させることから，ローパスフィルタの役割をします！このことから，ω=1/Tを遮断周波数と呼ぶ場合がありますので，これについてもしっかりと覚えておきましょう(^^)/
図15 一次遅れのボード線図
一次進み
図16が一次進みの伝達関数になります！
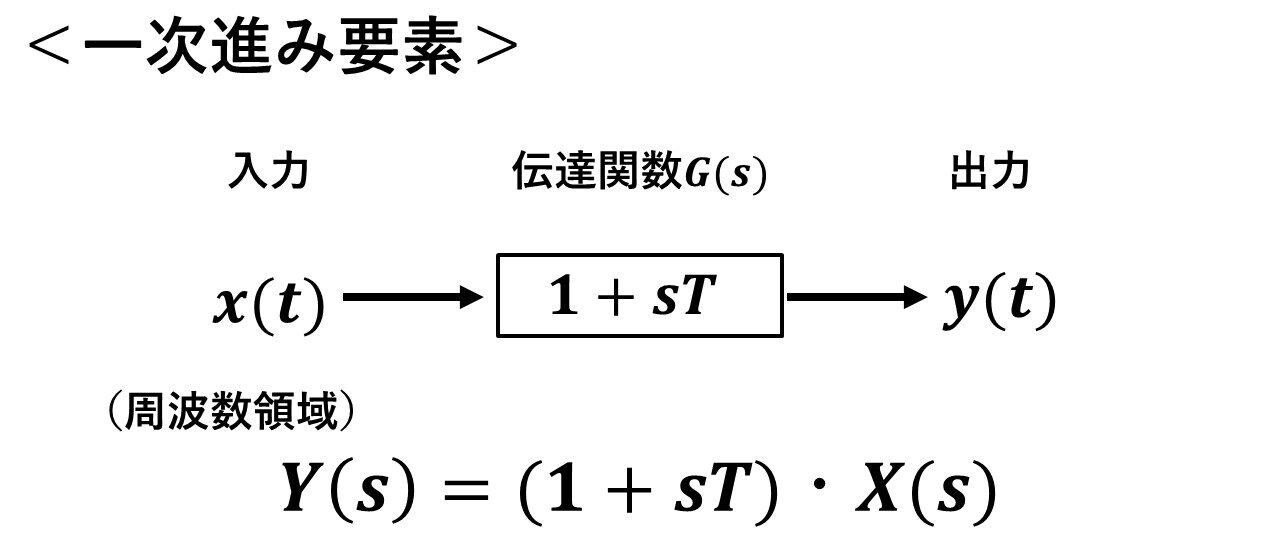図16 一次進みの伝達関数
一次進みの単位ステップ応答
一次進みに単位ステップ信号u(t)を入力した場合の応答を見てみましょう！一次進みの単位ステップ応答の計算方法は以下の通りです！
図17 一次進みの単位ステップ応答の計算方法
一次進みの単位ステップ応答を図18に示します！
時間領域で考えると，一次進み1+sTの出力は，①1で入力信号をそのまま素通りさせた出力と，②sTで入力信号の微分（傾き）をとった出力の和になると考えることができます！そのため，図18のように，入力信号が変化する瞬間，つまりステップ信号を入力した瞬間は，入力信号の傾きが∞になるため，②の微分要素により出力が∞となり，それ以外の時間では入力信号が一定で傾き（微分）が0なので，①の入力信号をそのまま素通りした出力になることが分かります！
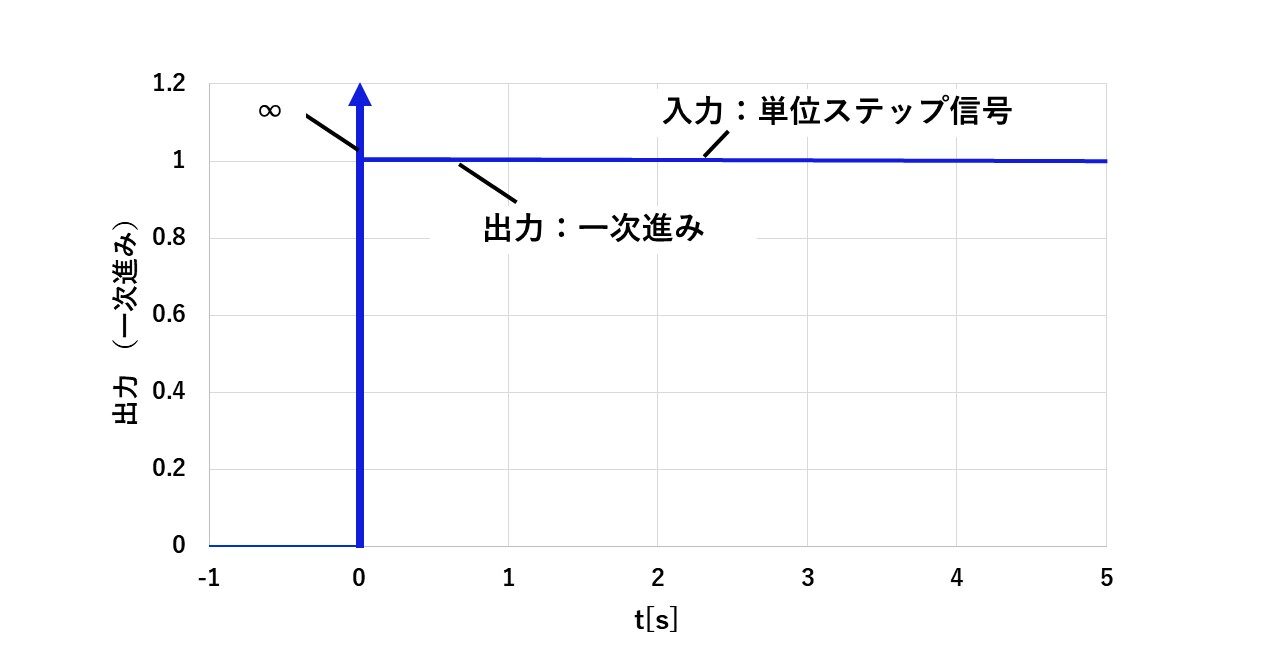図18 一次進みの単位ステップ応答
一次進みのボード線図
次に一次進みのボード線図を求めてみましょう！一次進みのボード線図は，図19のように求めることができます！
図19 一次進みのボード線図の計算方法
図20が，一次進みのボード線図になります！一次遅れと同様に，一次進みのボード線図でも，ωTの大小関係によってゲイン特性や位相特性が変わり，折点周波数ω=1/Tの点を境に特性が大きく変化します！一次遅れ同様，ωTの大小関係によって，ゲイン特性や位相特性がどのように近似できるかは非常に重要になりますので，しっかりと押さえておきましょう(^^)/
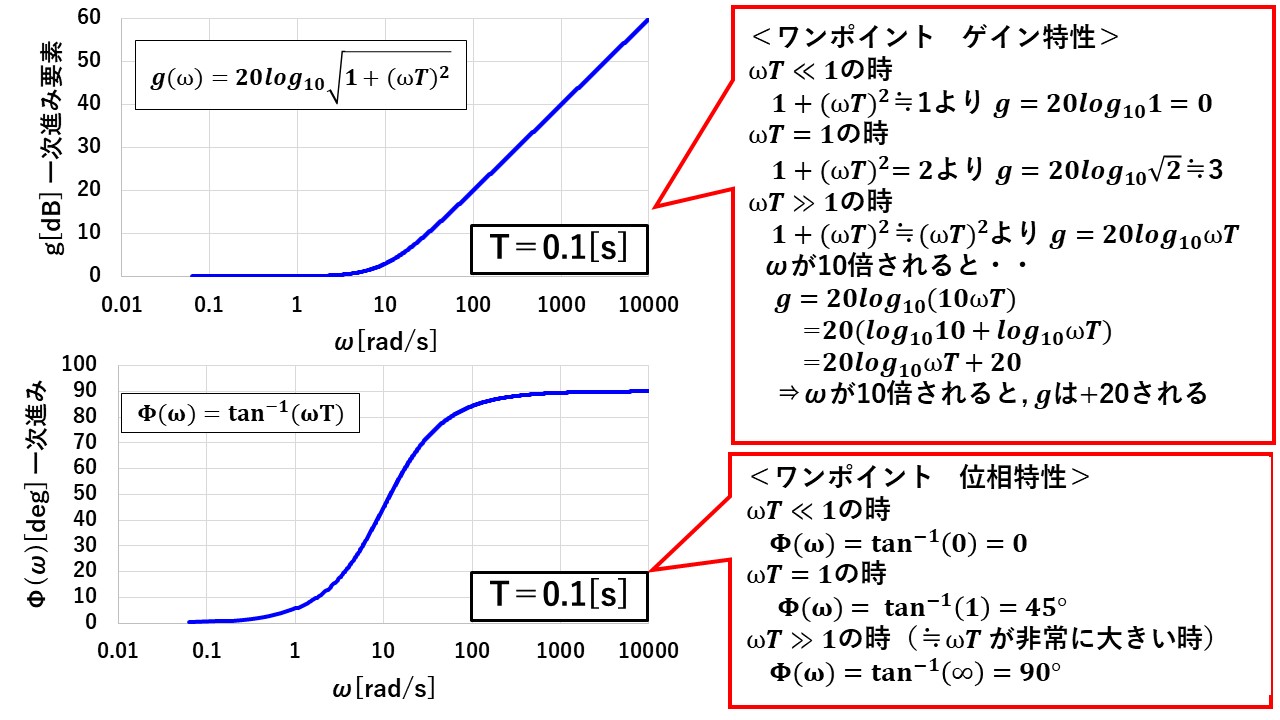図20 一次進みのボード線図
（ちょっと休憩）理系大学生が学生時代に必ずやっておくべき5つのこと！！
大学生の皆さん！勉強お疲れ様です(>_<) 以下の記事は，私が理系の大学生の皆さんに向けて，社会人になる前にやっておいた方がよいことを5つに厳選して書いた記事です！これらは，私が社会人になって，「学生時代にこれをやっておいて本当に良かった！」と心から思うことや，「学生時代に何でこれをやっておかなかったんだろうか・・・」と超絶後悔していることなどを厳選しています(^^)/勉強の休憩がてらに，是非見てみてください！
不完全微分
図21が不完全微分の伝達関数になります！
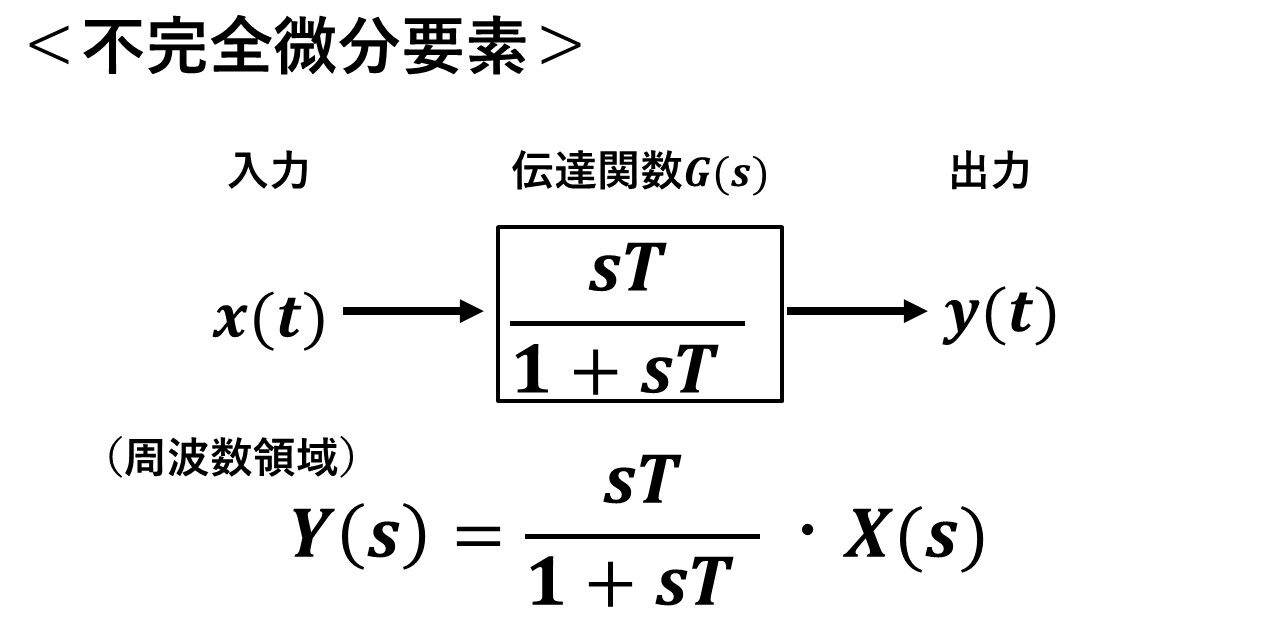図21 不完全微分の伝達関数
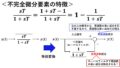
ここで，図22に不完全微分の特徴を示します！不完全微分は，数式を変形すると，図22のように，①入力信号を素通りさせた出力から，②一次遅れにより低周波数成分を抽出した信号を，引き算したものになることが分かります！この性質は，不完全微分の性質を理解する上で非常に重要になりますので，しっかりと押さえておきましょう(^^)/
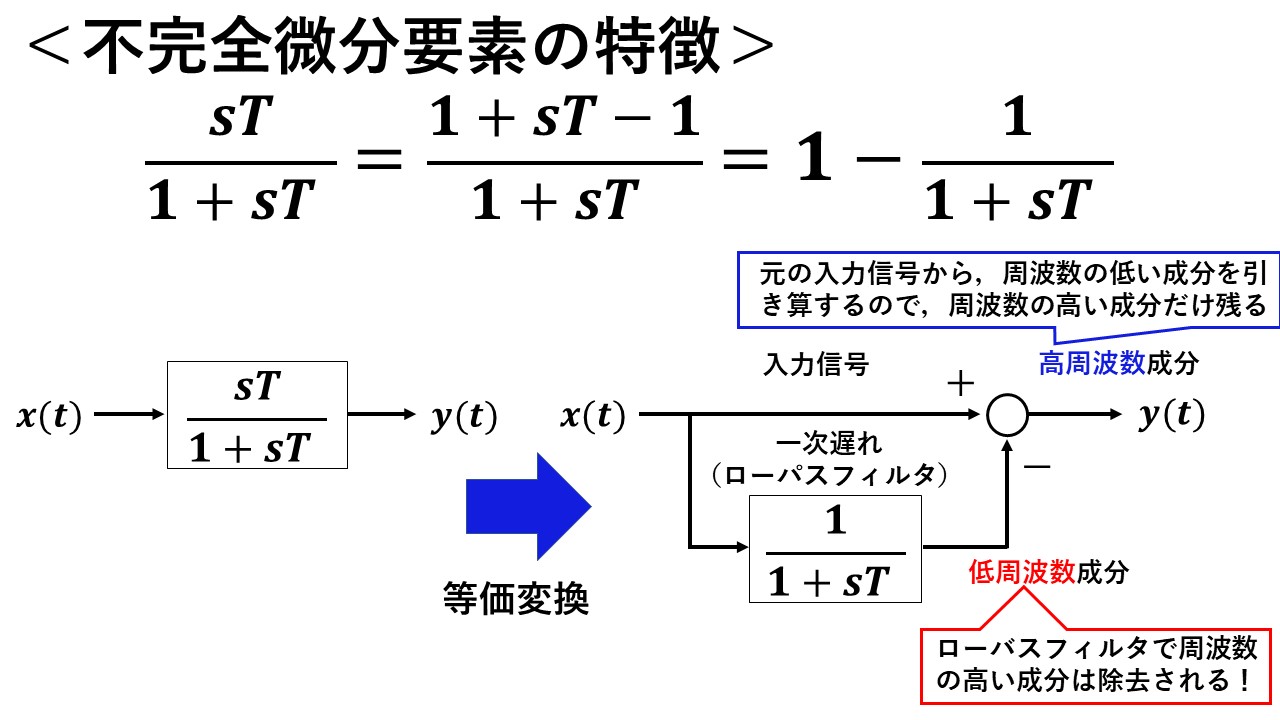図22 不完全微分の特徴
不完全微分の単位ステップ応答
不完全微分の単位ステップ応答の計算方法は以下の通りです！
図23 不完全微分の単位ステップ応答の計算方法
不完全微分の単位ステップ応答を図24に示します！図23の計算結果の通り，不完全微分の単位ステップ応答は，y(t)=exp(-t/T)になりますので，ステップ信号が入力された時に大きな値をとって，それ以降は時定数Tで減衰していきます！
図24の波形からも，不完全微分は①入力信号を素通りさせた出力から，②一次遅れにより低周波数成分を抽出した信号を引き算したものになっていることが確認できますね(^^)/
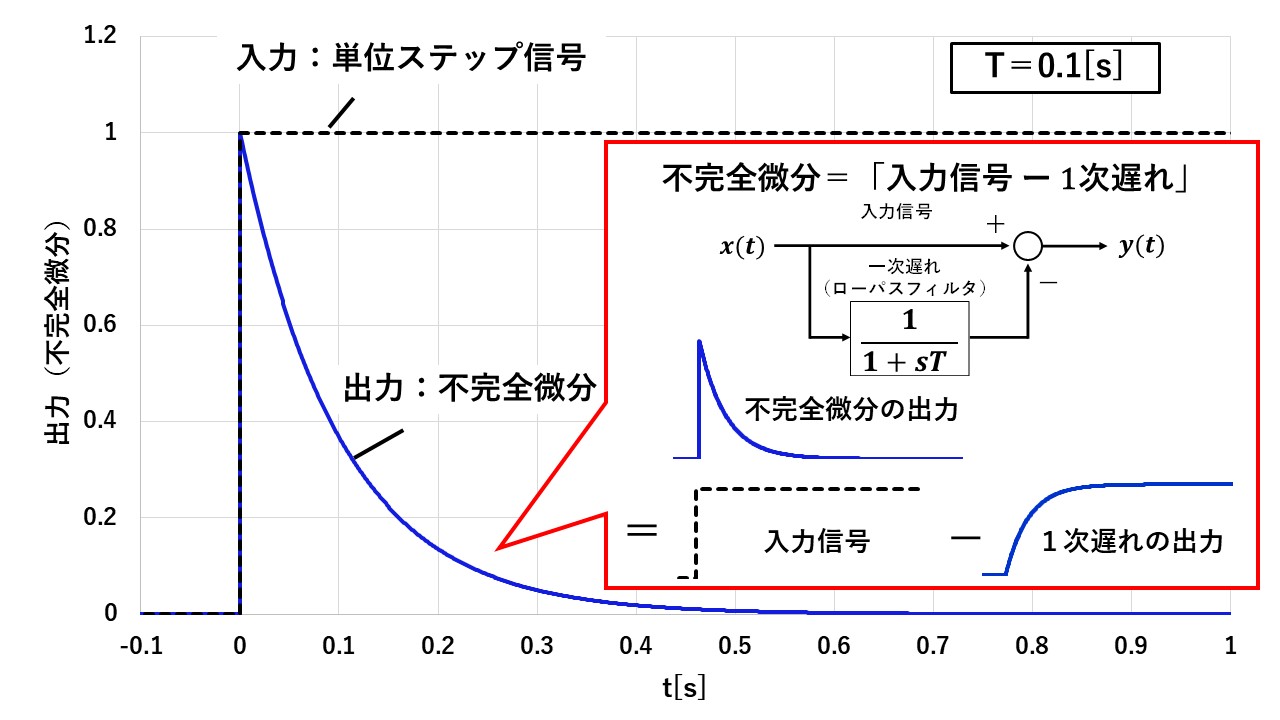図24 不完全微分の単位ステップ応答
不完全微分のボード線図
次に不完全微分のボード線図を求めてみましょう！不完全微分のボード線図は，図25のように求めることができます！ゲイン特性の縦軸は20log10|G(jω)|でdB表示になっていることに注意しましょう(^^)/
図25 不完全微分のボード線図の計算方法
図26が，不完全微分のボード線図になります！同図のワンポイントに書いたように，不完全微分は，微分ブロックと一次遅れブロックの積と考えることができるので，不完全微分のゲイン特性と位相特性は，これら二つのブロックの特性の足し合わせで決まることが分かります！
なお，図26の不完全微分のゲイン特性を見ると，ω=1/Tよりも低い周波数成分に対しては，ゲインが小さく出力が大きく減衰するのに対し，ω=1/Tよりも高い周波数成分についてはゲインが0で，ほぼそのまま通過することが分かります！これは，不完全微分がハイパスフィルタとして機能することを意味しており，図22と同じ結果になっています(^^)/
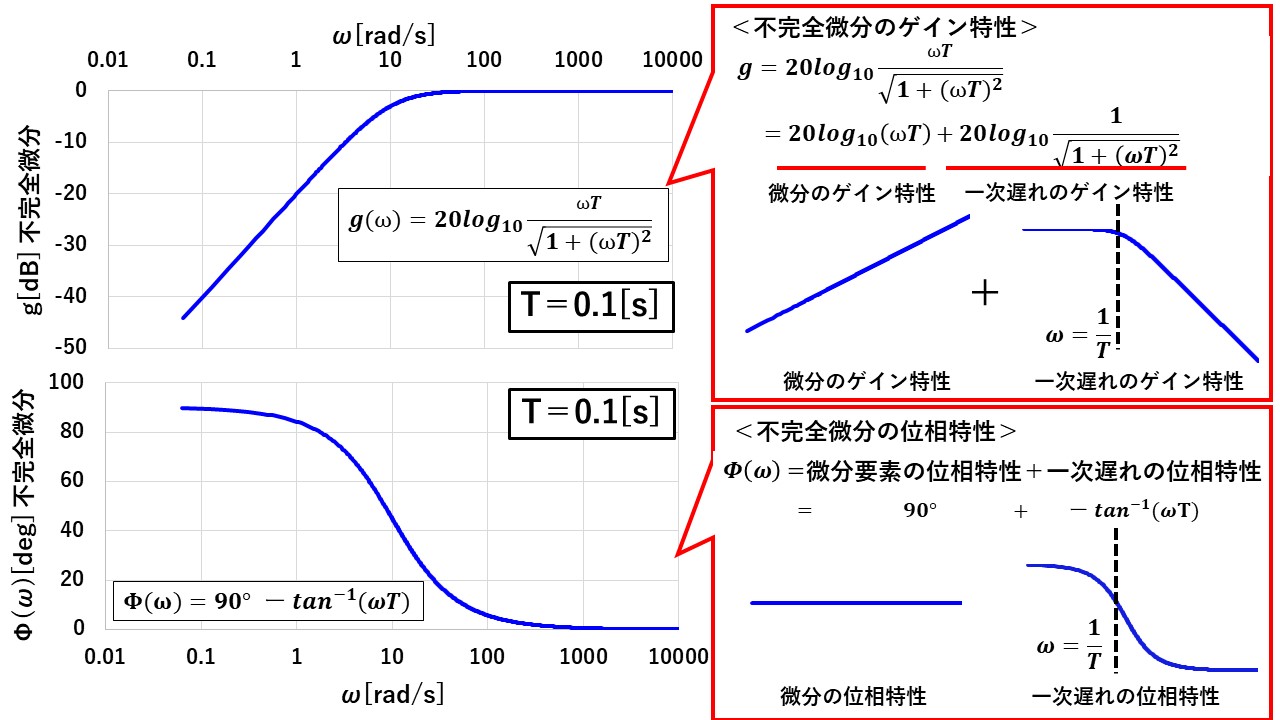図26 不完全微分のボード線図
一次進み遅れ要素（位相進み遅れ補償）
図27が一次進み遅れ要素の伝達関数になります！
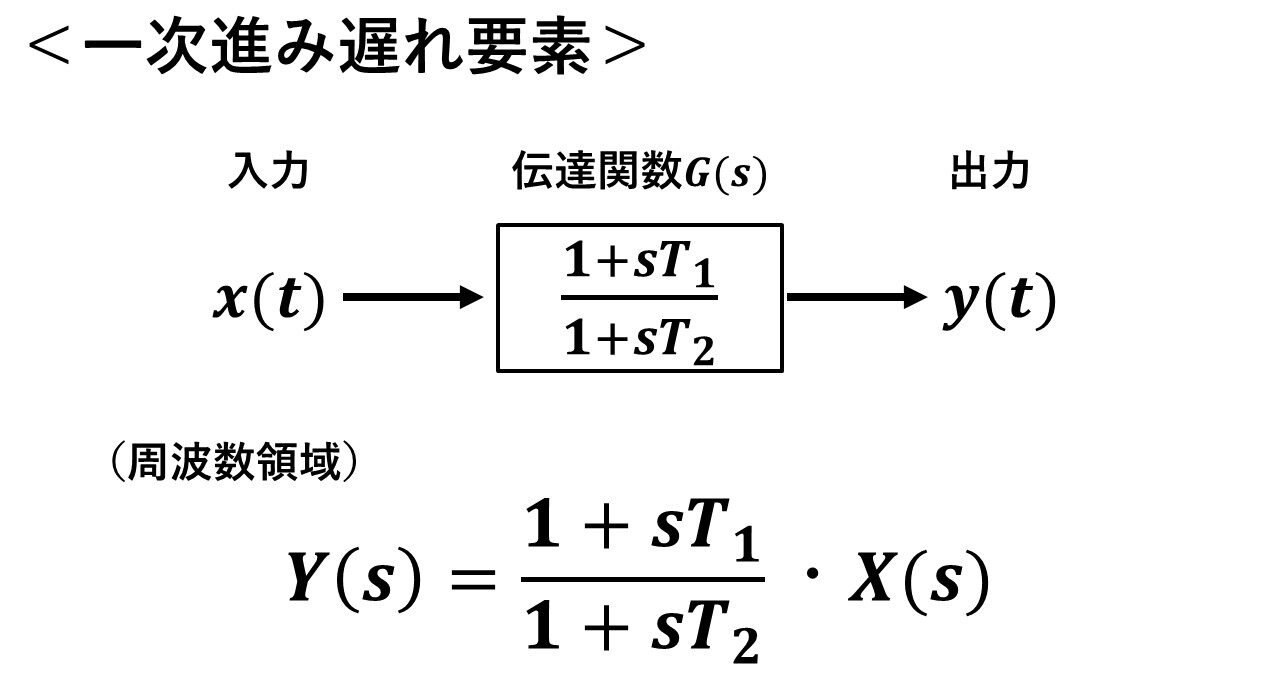図27 一次進み遅れ要素の伝達関数
一次進み遅れ要素（位相進み遅れ補償）の単位ステップ応答
実際に，一次進み遅れ要素に単位ステップ信号u(t)を入力した場合の応答を見てみましょう！一次進み遅れ要素の単位ステップ応答の計算方法は以下の通りです！式の見通しを良くするために，以下のようにβ（＝T1/T2）を定義します！実はこのβが1より大きいか小さいかで，単位ステップ応答の挙動が変わります(^^)/
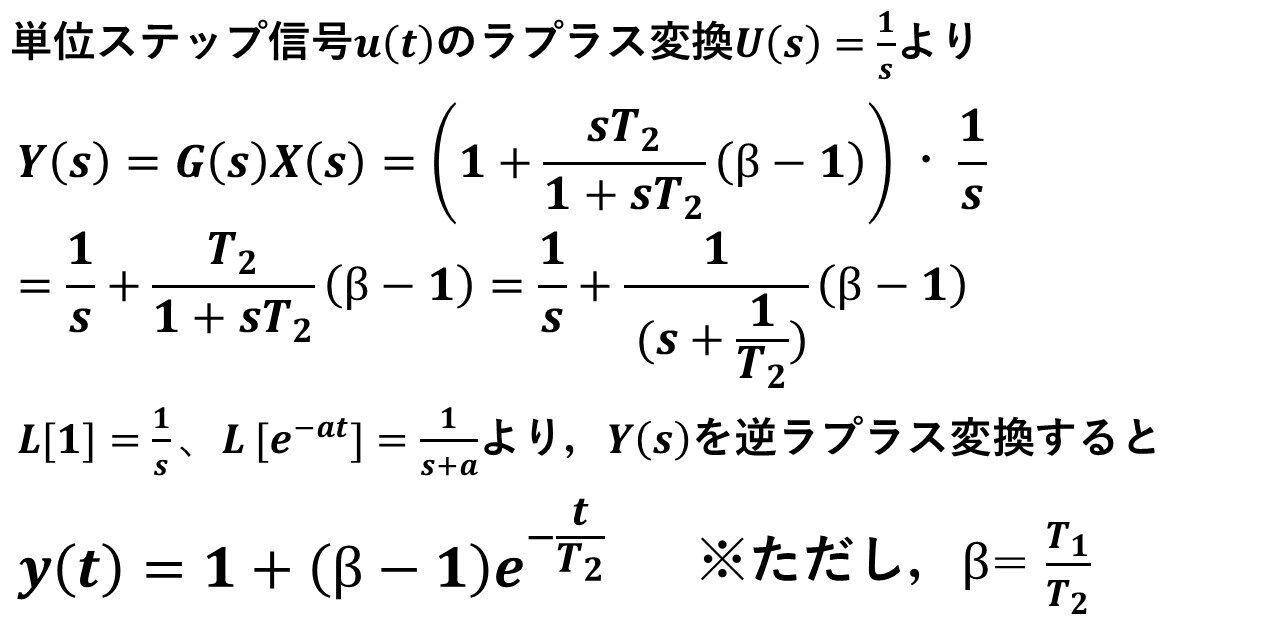図28 一次進み遅れ要素の単位ステップ応答の計算方法
図29にβ>1の場合の一次進み遅れ要素の単位ステップ応答を示し，図30にβ<1の場合の応答を示します！
上述した通り，一次進み遅れ要素の単位ステップ応答は，βの大きさによってその波形の様子が変わります！β>1の場合，ステップ信号を入力した時に入力よりも出力の方が大きくなるのに対し，β<1の場合は，出力の方が小さくなります！
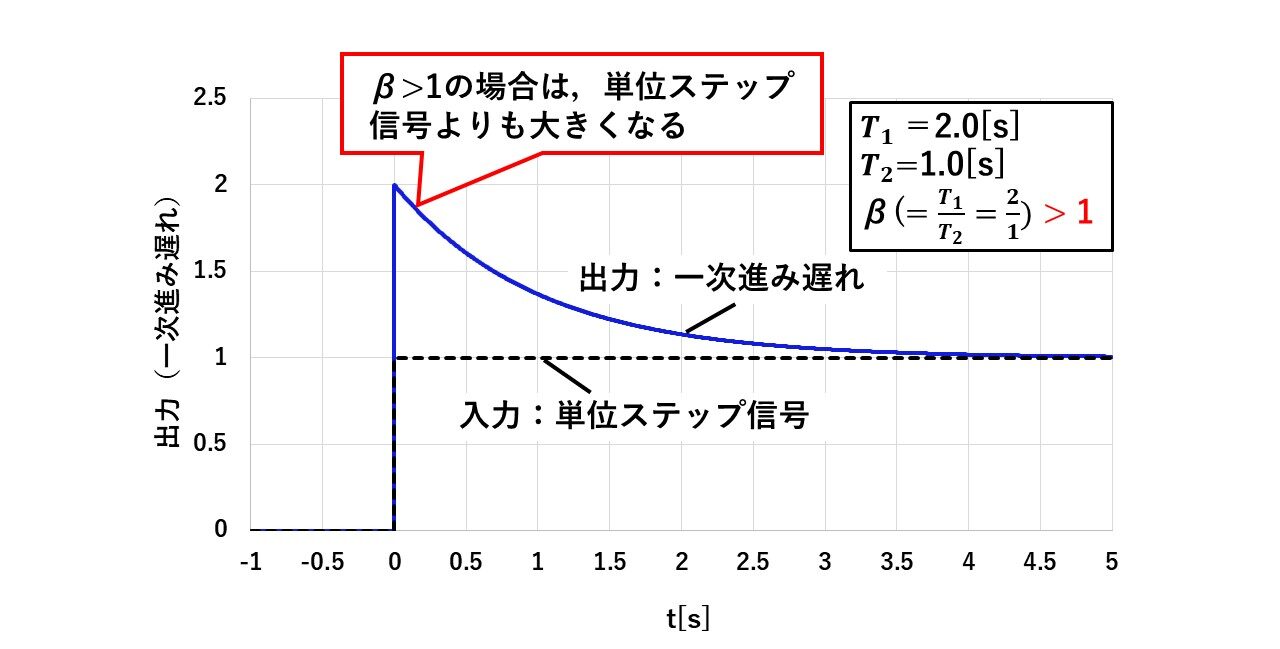図29 一次進み遅れ要素の単位ステップ応答（β＞１の場合）
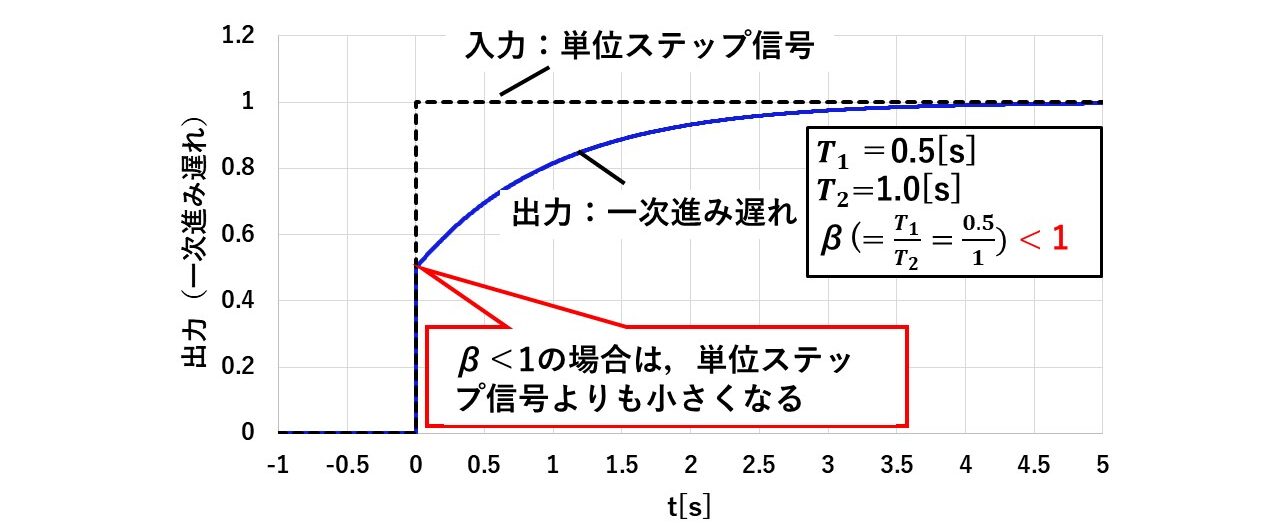図30 一次進み遅れ要素の単位ステップ応答（β＜１の場合）
一次進み遅れ要素（位相進み遅れ補償）のボード線図
次に一次進み遅れ要素のボード線図を求めてみましょう！一次進み遅れ要素のボード線図は，図31のように求めることができます！ボード線図については，T1とT2の大小関係（＝βが1より大きいか小さいかと同じ）によって，ゲイン特性や位相特性の概形が変わります！
図31 一次進み遅れ要素のボード線図の計算方法
図32に，T1>T2（前述のβでは，β>1）の場合のボード線図を示し，図33にT1>T2(β<1)の場合のボード線図を示します！いずれの条件においても，一次進み遅れ要素のゲイン特性・位相特性は，一次進み要素と一次遅れ要素の和によって表すことができ，進み要素と遅れ要素の折点周波数（ω＝1/T）の大小関係によって，その概形が変わります！進み要素の折点周波数ω＝1/T1の方が低い場合（図32）は，ゲインは大きく，位相は進むのに対し，遅れ要素の折点周波数ω＝1/T2の方が低い場合（図33）は，ゲインは小さく，位相は遅れます(^^)/
このように，一次進み遅れ要素の特性は，T1やT2の大小関係によって大きく変化することはしっかりと押さえておきましょう(^^)/
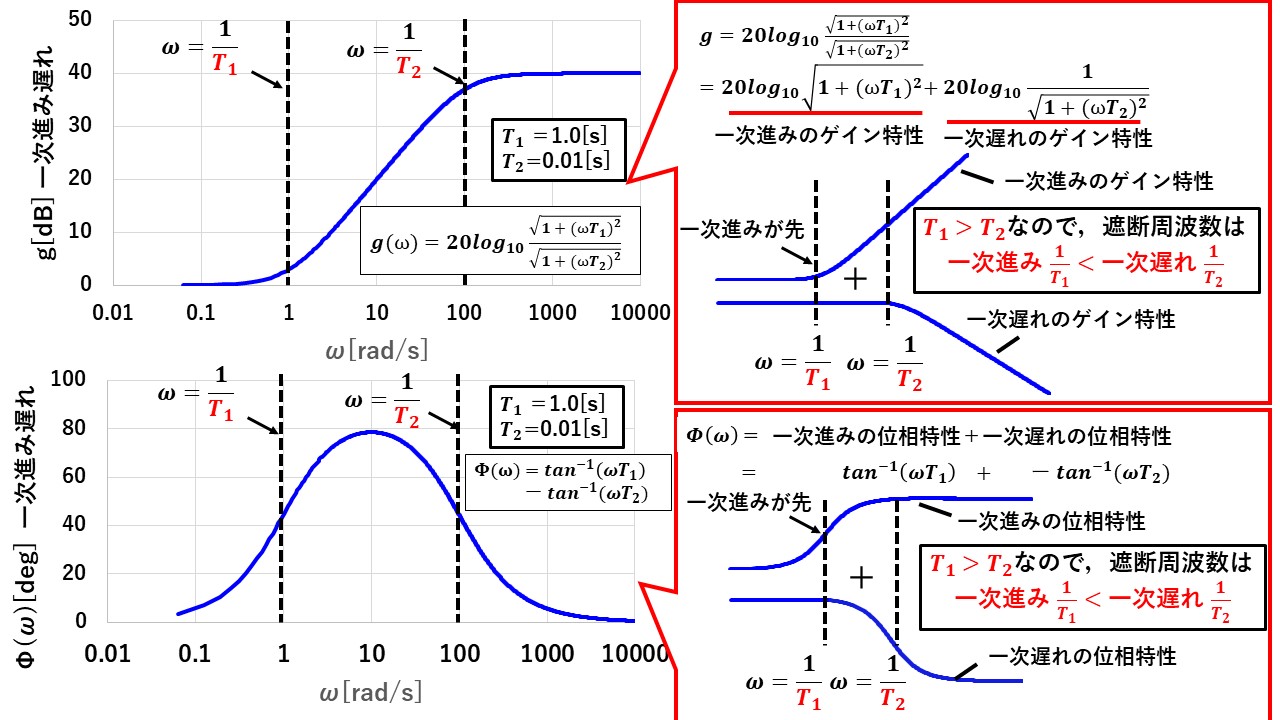図32 一次進み遅れ要素のボード線図 （T1>T2の場合 ＝ β>1の場合）
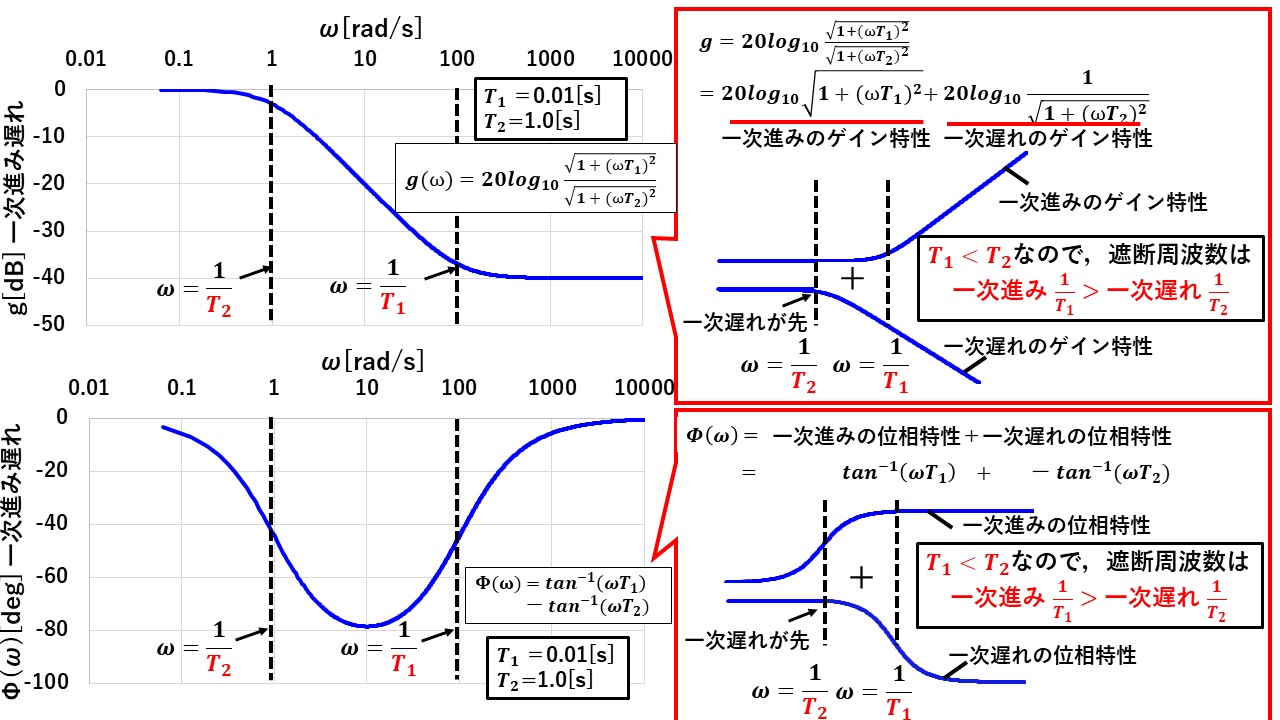図33 一次進み遅れ要素のボード線図 （T1<T2の場合 ＝ β<1の場合）
今回の記事はここまでです！お疲れさまでした(^^)/
