こんにちは，ハヤシライスBLOGです！今回は制御工学等で主に扱う線形時不変システム（LTIシステム：Linear Time-Invariant system）について，分かりやすく解説します！特に，線形システムとはそもそも何かであったり，線形システムの大きな特徴の一つである重ね合わせの理やたたみこみ積分について，分かりやすく解説します(^^)/
線形時不変システム（LTIシステム）とは
線形時不変システム（LTIシステム：Linear Time-Invariant system）とは，読んで字のごとく，線形でかつ時不変なシステムのことです。線形システムとは，重ね合わせの理が成り立つシステムのことであり，時不変システムとは，システムの性質が時間に依らないシステムのことです！これだけではよく分からないと思いますので，一つずつ見ていきましょう(^^)/
図1 線形時不変システム（LTIシステム）とは
時不変システムとは
時不変システムとは，一言でいえば，システムの性質が時間に依らないシステムのことです！もう少し簡単に言えば，システムに信号が入力されるタイミングが変わっても，その入力信号の波形が同じであれば，出力も波形の形は変わらず，タイミングだけがずれるというものです！これが時不変システムの特徴です(^^)/
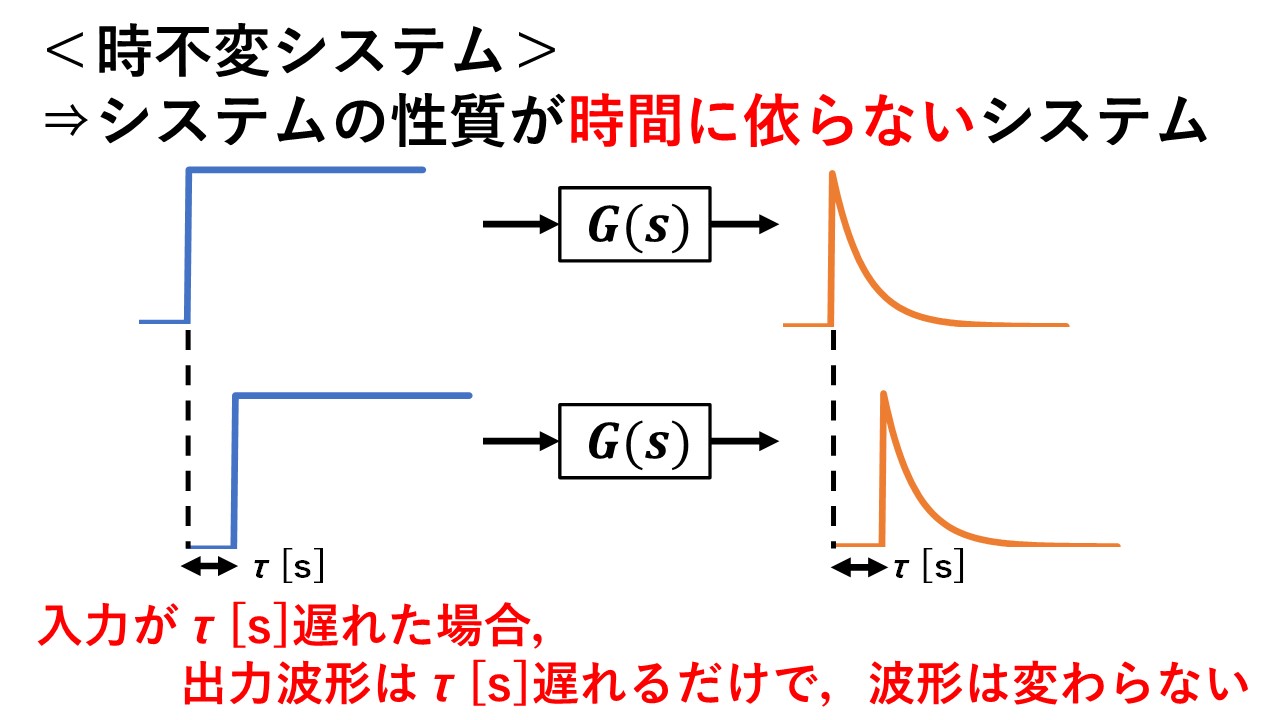図2 時不変システムとは
線形システムとは
線形システムとは，一言でいえば，重ね合わせの理が成り立つシステムのことです！重ね合わせの理が成り立つシステムとは，あるシステムに入力される2つの信号をx1、x2とし，それぞれの出力がy1、y2であるとした時，ax1＋bx2を入力した時の出力がay1+by2になるシステムのことです！少し分かりにくいので，もう少し補足します！
要するに，重ね合わせの理が成り立つシステム，つまり線形システムとは，①入力される信号がa倍されたら，出力も単純にa倍される，②複数の信号が同時に入力された場合の出力は，それぞれの入力信号に対する出力の足し合わせで求めることができる，これが線形システムになります！
図3 線形システムとは
線形システムで，重ね合わせの理が成り立つことを確認してみよう！
実際に，線形システムで重ね合わせの理が成り立つのかを，図4のようなゲインブロックを例に考えてみましょう！ゲインをKと設定しているので，入力信号をxとすると，その出力yはy=Kxになります
●まず，入力信号をa倍してみましょう！その出力は，y=K(ax)=a(Kx)となり，x入力時の出力y=Kxをa倍したものになることが分かります！
●次に，複数の信号x1とx2を同時に入力した場合の出力を求めてみましょう！すると，その出力は，y=K(x1+x2)=Kx1+Kx2となります！これはx1入力時の出力Kx1と，x2入力時の出力Kx2の和になっていますね(^^)/
以上から，ゲインブロック（線形システム）では重ね合わせの理が成り立つことが確認できました(^^)/
図4 線形システムの例（ゲインブロック）
非線形システムで，重ね合わせの理が成り立たないことを確認してみよう！
次に，非線形システムでは重ね合わせの理が成り立たないことを確認してみましょう！
非線形システムの代表として，図5のようなリミッタブロックを考えます！リミッタの上限値をH，下限値をLと設定しているので，入力信号をxとすると，その出力yは入力信号xの大きさに応じて，H or x or Lに場合分けされます！
●先程のゲインブロックと同様に，入力信号をa倍してみましょう！変数だと分かりにくいので，簡単のため，x=3，H=5，a=2とします！
すると，x=3の時はリミッタの上限値5に制約されないので，出力は3になりますが，xを2倍して6を入力した場合は，リミッタの上限値5に制約されるので，その出力は5になります！もし重ね合わせの理が成り立つのであれば，入力x=3を2倍にしているので，その出力はy=6になるはずですが，そうはなっていませんね！
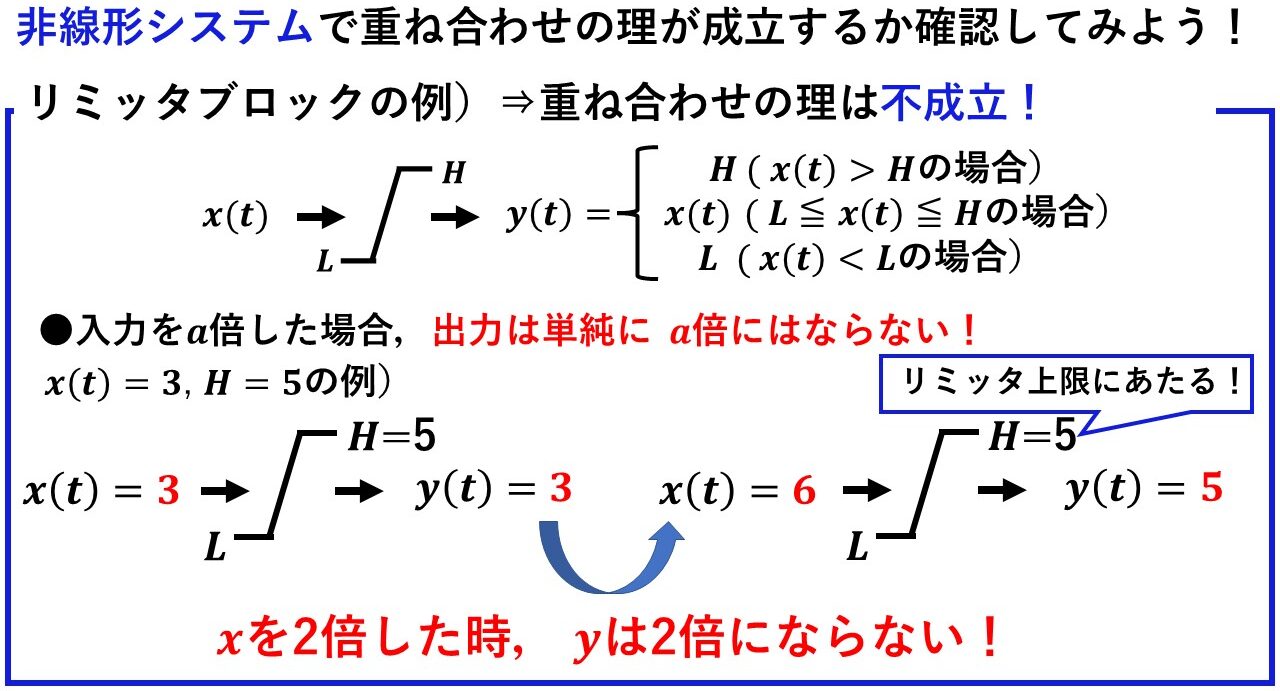図5 非線形システムの例①（リミッタブロック）
●次に，図6のように複数の信号x1～x3を同時に入力した場合の出力を求めてみましょう！ここでも簡単のため，H=5とします！まず，x1=1，x2=2，x3=3の3つの信号のそれぞれの出力を求めると，いずれもリミッタ上限値5に制約されず，y1=1, y2=2，y3=3となります！では，x1～x3の3つの信号を同時に入力した場合はどうでしょうか？この場合は，入力がx1+x2+x3=6になるので，リミッタ上限値5に制約され，その出力はy=5になります！もし重ね合わせの理が成り立つのであれば，出力はy1+y2+y3=6になるはずですが，そうはなっていませんね！
以上から，リミッタブロック（非線形システム）では重ね合わせの理が成り立たないことが確認できました(^^)/
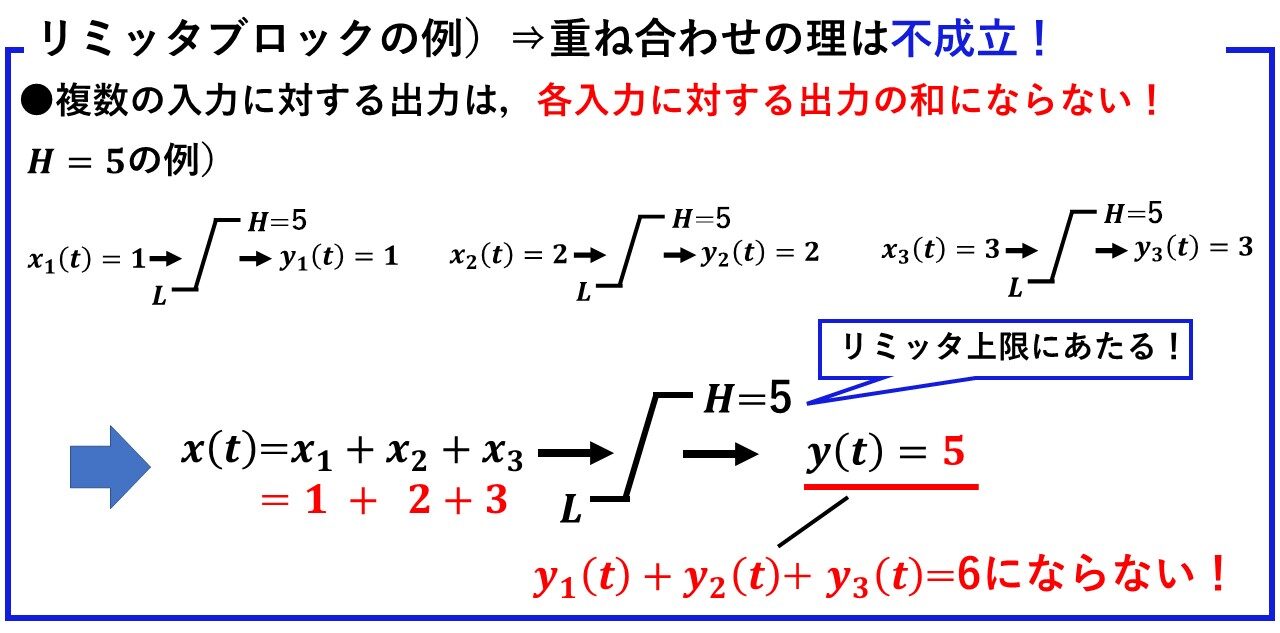図6 非線形システムの例②（リミッタブロック）
（ちょっと休憩）理系大学生が学生時代に必ずやっておくべき5つのこと！！
大学生の皆さん！勉強お疲れ様です(>_<) 以下の記事は，私が理系の大学生の皆さんに向けて，社会人になる前にやっておいた方がよいことを5つに厳選して書いた記事です！これらは，私が社会人になって，「学生時代にこれをやっておいて本当に良かった！」と心から思うことや，「学生時代に何でこれをやっておかなかったんだろうか・・・」と超絶後悔していることなどを厳選しています(^^)/勉強の休憩がてらに，是非見てみてください！
LTIシステムの特徴とたたみこみ積分
LTIシステムとは何なのかが分かったところで，今度はLTIシステムの持つ特徴について理解しましょう！図7に示すように，実はLTIシステムでは，単位インパルス信号に対するシステムの出力，つまり単位インパルス応答が分かると，どんな入力に対するシステムの出力も計算によって求めることができます！つまり，一次遅れが何個あって，ゲインが何個あって，それらの設定がどうなっているか等のシステムの中身が分からなくても，単位インパルス応答さえ分かってしまえば，あらゆる入力に対して出力信号を予想できてしまうのです！すごいですね！(>_<)
なぜこんなことができるのかというと，
それは線形時不変システムだからです！非線形システム等ではこれはできません！以降で解説します(^^)/
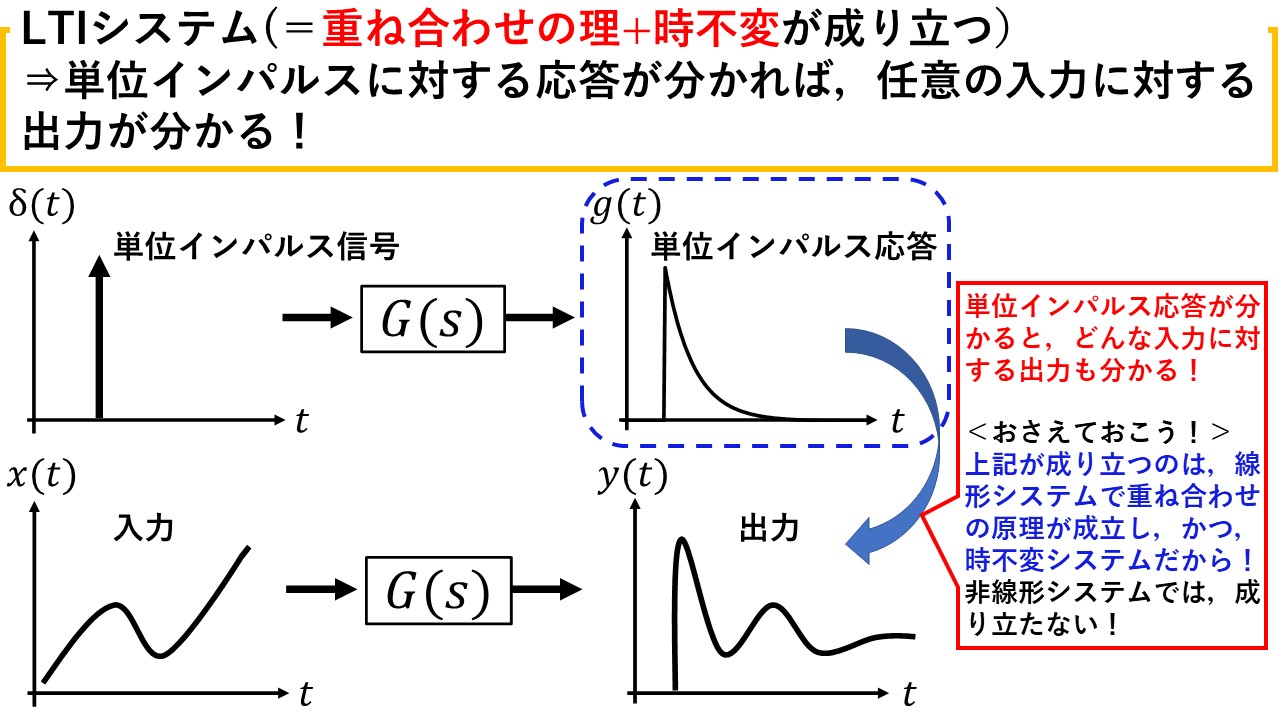図7 LTIシステムでは，単位インパルス応答が分かれば出力が予想できる！
まずはイメージをつかもう！
LTIシステムにおいて，なぜ単位インパルス応答が分かると任意の入力に対する出力が分かるのかを，イメージ図にしました(^^)/ 図8がそのイメージ図になります！この図を使って，どうやって単位インパルス応答から任意の入力に対する出力を求めることができるのかを順番にご説明します！
STEP①：入力信号をいくつかのインパルス信号に分解しよう！（入力信号をインパルス信号で表そう）
まず，入力信号x(t)を複数のインパルス信号を使って表すことを考えましょう！図8のように，大きさとタイミングが異なるインパルス信号をいくつか使えば，元の入力信号x(t)はこれらの足し合わせによって再現できそうですね(^^)/ まずはこのようにして，入力信号をいくつかのインパルス信号に分解しましょう！
STEP②：それぞれのインパルス信号に対して，インパルス応答を求めよう！
次に，それぞれのインパルス信号に対して，インパルス応答を求めましょう！この時に重要になるのが，線形システム，時不変システムの性質です！まず，線形システムでは重ね合わせの理が成り立ちますから，単位インパルス信号の大きさがx(m)倍されたら，インパルス応答の大きさも単純に単位インパルス応答をx(m)倍したものになります！また，時不変システムなので，インパルス信号が入力されるタイミングがm[s]だけずれても，インパルス応答のタイミングがm[s]ずれるだけです！
このように線形時不変システムの性質を使えば，たとえ大きさや入力タイミングが違うインパルス信号であっても，各々のインパルス応答を，単位インパルス応答を使って求めることができます(^^)/
STEP③：各々のインパルス応答を足し合わせて，出力を求めよう！
最後に，線形システムの性質である重ね合わせの理を使って，システムの出力y(t)を求めましょう！重ね合わせの理が成り立つシステムでは，複数の信号が同時に入力された場合の出力は，それぞれの入力信号に対する出力の足し合わせで求めることができました！STEP1により任意の入力x(t)は複数のインパルス信号が同時に入力されて作られた信号と考えることができますから，その出力y(t)は，それぞれのインパルス信号に対する出力の足し合わせで求めることができますね！！
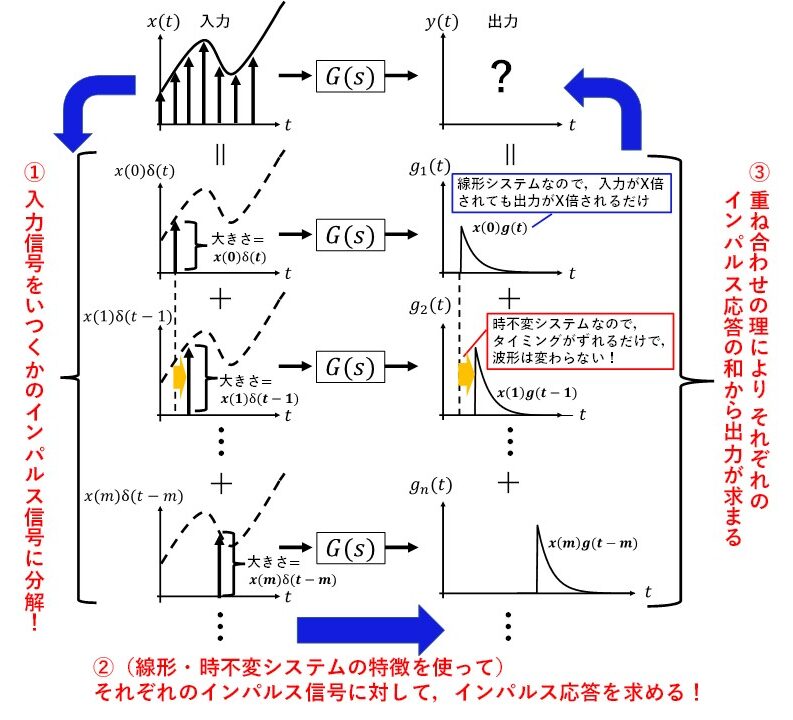
図8 単位インパルス応答から任意の入力に対する出力が分かる原理
たたみこみ積分の公式
図9にたたみこみ積分の公式を示します！出力信号y(t)が，入力信号x(t)と単位インパルス応答g(t)のみから求めることができるのが分かりますね(^^)/
なお，公式の右辺∫x(τ)g(t-τ)と図8で求めた各々のインパルス応答の和を見比べてみましょう！公式の右辺が，図8の各々のインパルス応答の和になっていそうというのが分かりますね(^^)/
図9 たたみこみ積分の公式
今回の記事はここまでです！少しでも皆さんの役に立っていれば嬉しいです(^^)/
（参考）線形システムやたたみこみ積分，ラプラス変換やフーリエ変換を演習問題を解きながら理解したい方にオススメの書籍
線形時不変システムでは，図8のイメージでシステムの出力を，たたみこみ積分により求めることができることをご説明しました(^^)/ ただ，実は図8はあくまでイメージ図であり，難しいことを少し省いて説明しています(笑) 例えば，図8の①の過程「入力信号をいくつかのインパルス信号で表す」という部分ですが，本記事ではまるで単位インパルス信号δ(t)の大きさが1であるかのように説明していますが，実際の単位インパルス信号の大きさは∞ですよね？そのため，実際にはインパルス信号の扱いをもう少しだけ真面目に考える必要があります！
以下の書籍では，この辺りの話を非常に丁寧に分かりやすく解説しています！たたみこみ積分，重ね合わせの理，線形時不変システムなどは勿論，フーリエ変換やラプラス変換，Z変換などについても演習問題多めに丁寧に解説していますので，是非読んでみてください(^^)/
