こんにちは，ハヤシライスBLOGです！今回は直流RC回路をラプラス変換を使って解いていきます！
直流RC回路
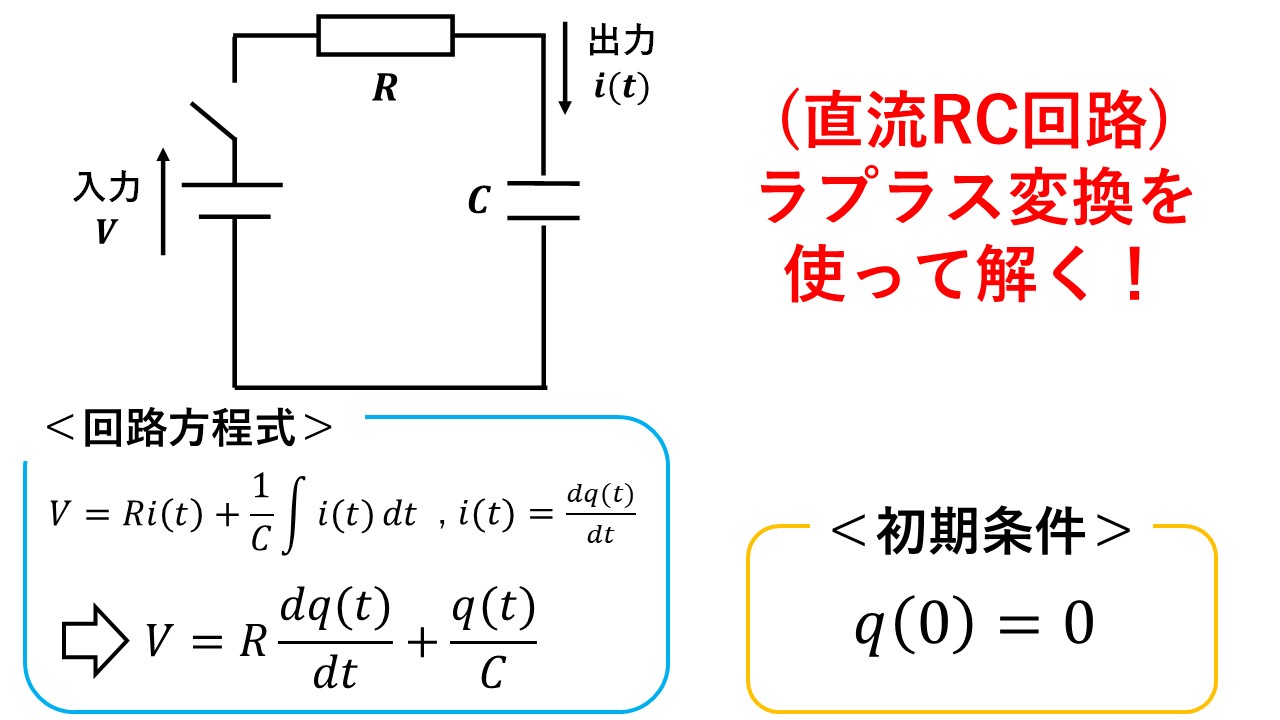
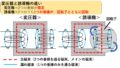
この記事では，図1のRC回路に，時刻0[s]で直流電源をつないだ場合の応答を，ラプラス変換を使って求めていきます！
図1 直流RC回路
なお，以下の記事では直流RL回路をラプラス変換を使って解く手順についても解説しております！良かったら参考にしてください(^^)/
ラプラス変換とは
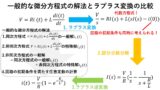
ラプラス変換とは，微分方程式を時間領域tではなく，周波数領域sで考えることで，微分方程式をより簡単に解くための手法です！
図2の通り，ラプラス変換すると，複雑な微分d/dtや積分∫dtが，s領域ではなんと単なるsの掛け算，割り算になります！つまり，時間領域tでは複雑な微分方程式であったものが，周波数領域sでは代数方程式になり，四則演算で解くことができます(^^)/
図2 ラプラス変換のメリット
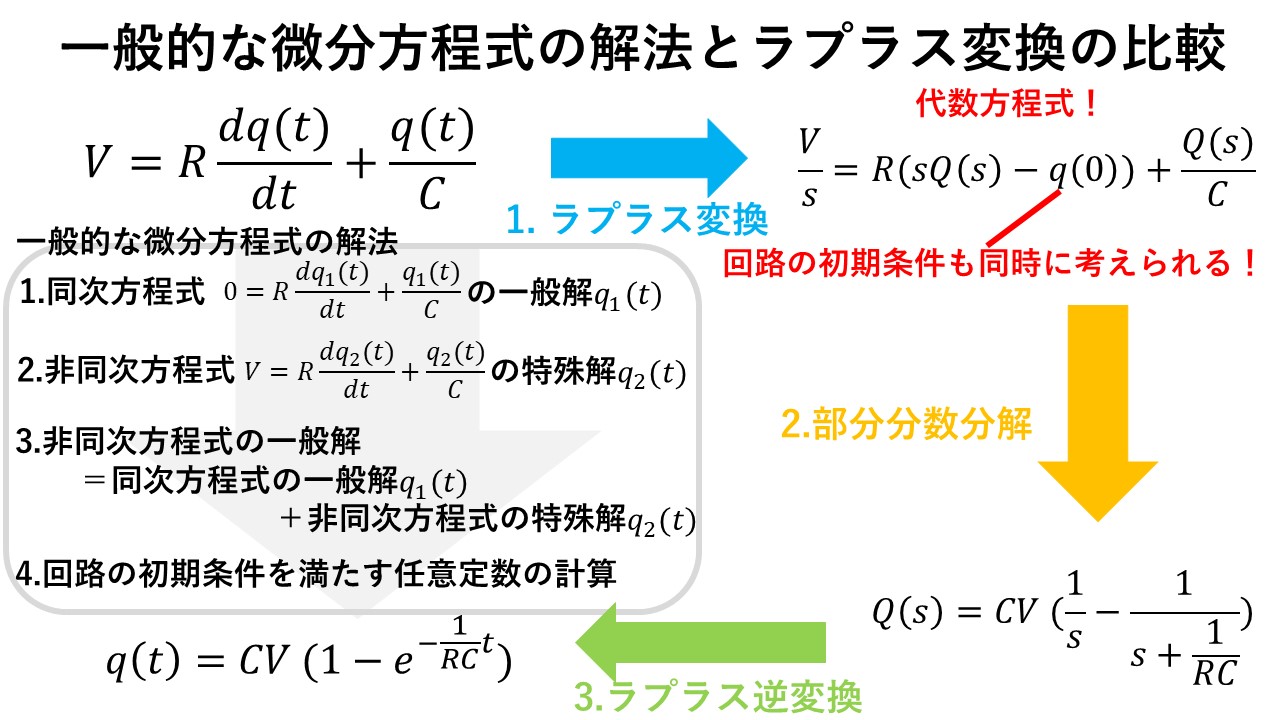
図3に，一般的な微分方程式の解法とラプラス変換による計算の比較を示します！ 一般的な微分方程式の解法では，同次方程式や非同次方程式などを微分を使って解くのに対し，ラプラス変換では代数的に解くので，計算が楽になります！なお，一般的な微分方程式の場合は，最後に回路の初期条件を考慮しますが，ラプラス変換では初期条件も含めて一気に解いてしまうという違いもあります(^^)/
なお，一般的な微分方程式の解法を使って，どうやって直流RC回路を解くのかが知りたい方は，以下の記事を参考にしてください(^^)
図3 一般的な微分方程式による解法とラプラス変換の比較
計算手順
ラプラス変換を使った直流RC回路の計算手順は以下の通りです！全部で3つのステップからなっています！ 1つずつ順番に解説していきます(^^)/
図4 計算手順
Step1：微分方程式をラプラス変換しよう！
まず，回路方程式をラプラス変換します。図5の青枠で囲んだ公式を使ってラプラス変換すると，回路方程式は代数方程式になり，微分がなくなっているのが分かりますね！ また，回路の初期条件「時刻0[s]での電荷は0」についてもここで考えてしまいます！
図5 回路方程式をラプラス変換する
Step2：部分分数分解をしよう！
続いて，ラプラス逆変換できる形にするため，部分分数分解を行います！
部分分数分解の手順としては，
①：まずラプラス逆変換できる形を予め把握しておきます！この例で，1/s，1/(s+1/(RC))に分ければ，ラプラス逆変換できそうだというのが分かればよいです！なお，これにはある程度公式の暗記が必要ですが，ラプラス変換の公式はそこまで多くなく，また使う公式は大体いつも同じですから，覚えてしまいましょう(^^)/
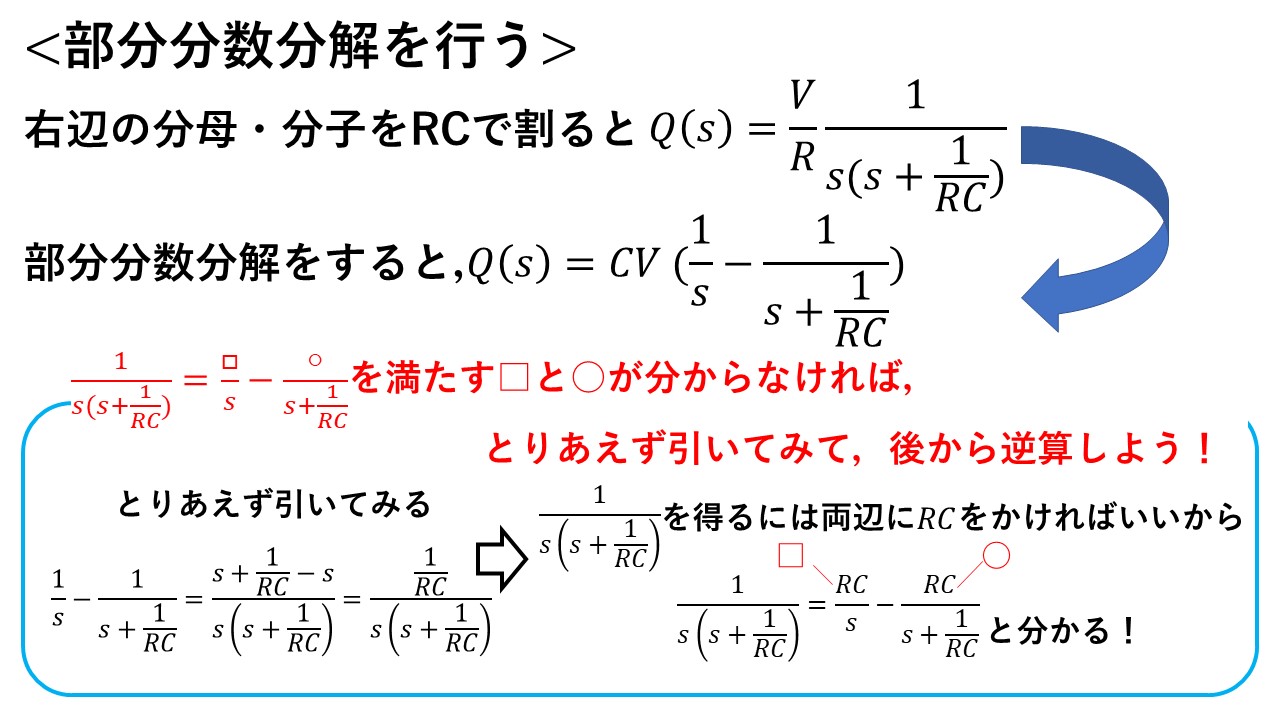
②：次に，どうやったら①の逆変換できる形に式変形できるかを考えます！つまり，
1/(s(s+1/(RC)))＝□/sー○/(s+1/(RC))
を満たす□と○の係数が分かれば，元の式をラプラス逆変換できる形に変形できます！この□と○を求める方法については公式なんかもありますが，私のオススメは「とりあえず1/sー1/(s+1/(RC)）を計算してみる」です！すると，これを計算した結果は元の式1/(s(s+1/(RC)))のX倍 (この例では, X=1/(RC) )になりますので，1/sー1/(s+1/(RC)）を計算した式の両辺を，逆にXで割れば，□と○の係数が分かります！
図6 部分分数分解を行う
Step3：ラプラス逆変換しよう！
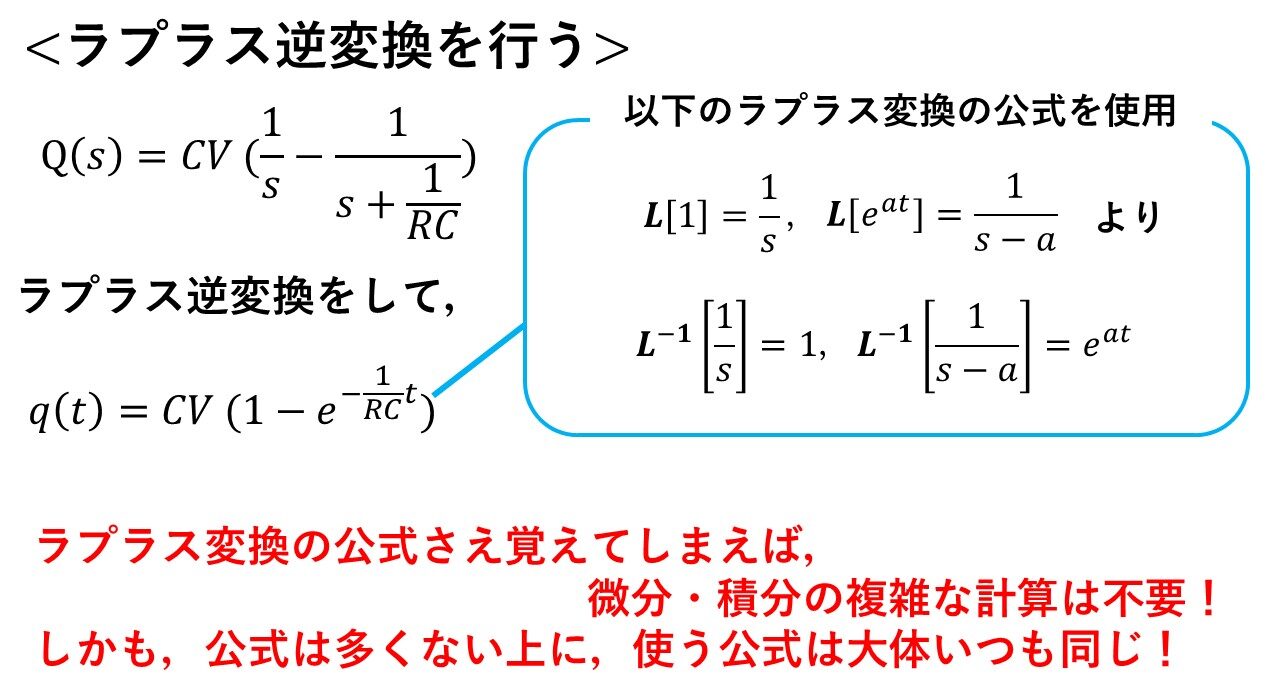
最後にラプラス逆変換して，最終的な解を求めましょう！ラプラス変換の公式を使って，最終的な解を簡単に求めることができます(^^)/
このように，ラプラス変換はある程度公式を覚えてしまえば，微分・積分の複雑な計算をすることなく，簡単に解にたどり着きます！そして，公式の数もそんなに多くない上に，普段使う公式も限られているので，比較的簡単に微分方程式を解くことができます(^^)/
図7 ラプラス逆変換を行う
直流RC回路の特徴
図8に，直流RC回路におけるコンデンサの電荷qとコンデンサ電圧vcを示します！スイッチをONにした瞬間は電荷q(t)は0なので，vc(t)=q(t)/Cより，コンデンサ電圧vcも0となります(^^)/
スイッチをONにしてからは，コンデンサ電圧vcが電源電圧Vと等しくなるまで，コンデンサに電荷が充電されます(^^)/
図8 直流RC回路の電荷とコンデンサ電圧
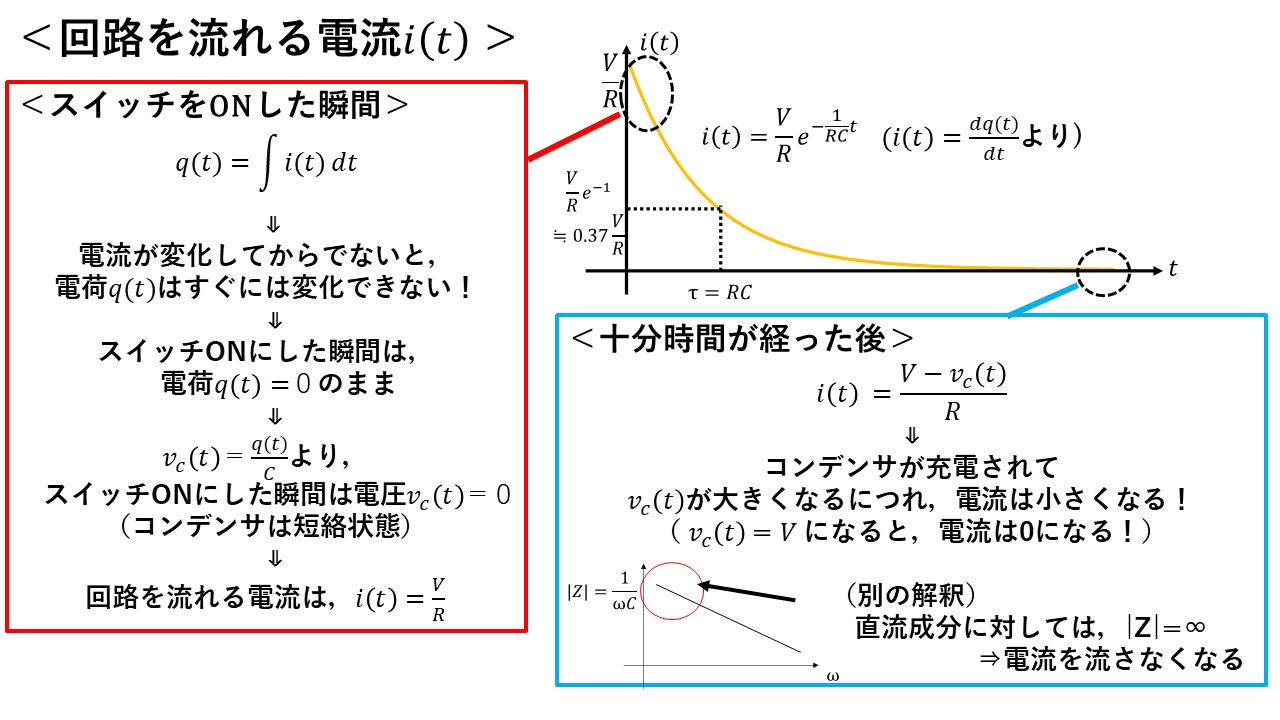
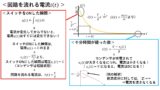
続いて，電流iのグラフを見てみましょう！ 電流iは，i(t)=dq(t)/dtより，電荷の式を時間微分すれば求めることができます！ その結果が，図9になります！
スイッチをONにした瞬間は，コンデンサの電荷と電圧は0のままなので，コンデンサは一時的に短絡状態とみなせます！したがって，回路には抵抗Rしかありませんので，流れる電流はI=V/Rとなります(^^)/
十分時間が経ち，定常状態になると，コンデンサの電圧が電源電圧と同じ大きさになり，抵抗両端にかかる電圧が等しくなり，回路に電流は流れなくなります(^^)/
図9 直流RC回路の電流
コンデンサの性質
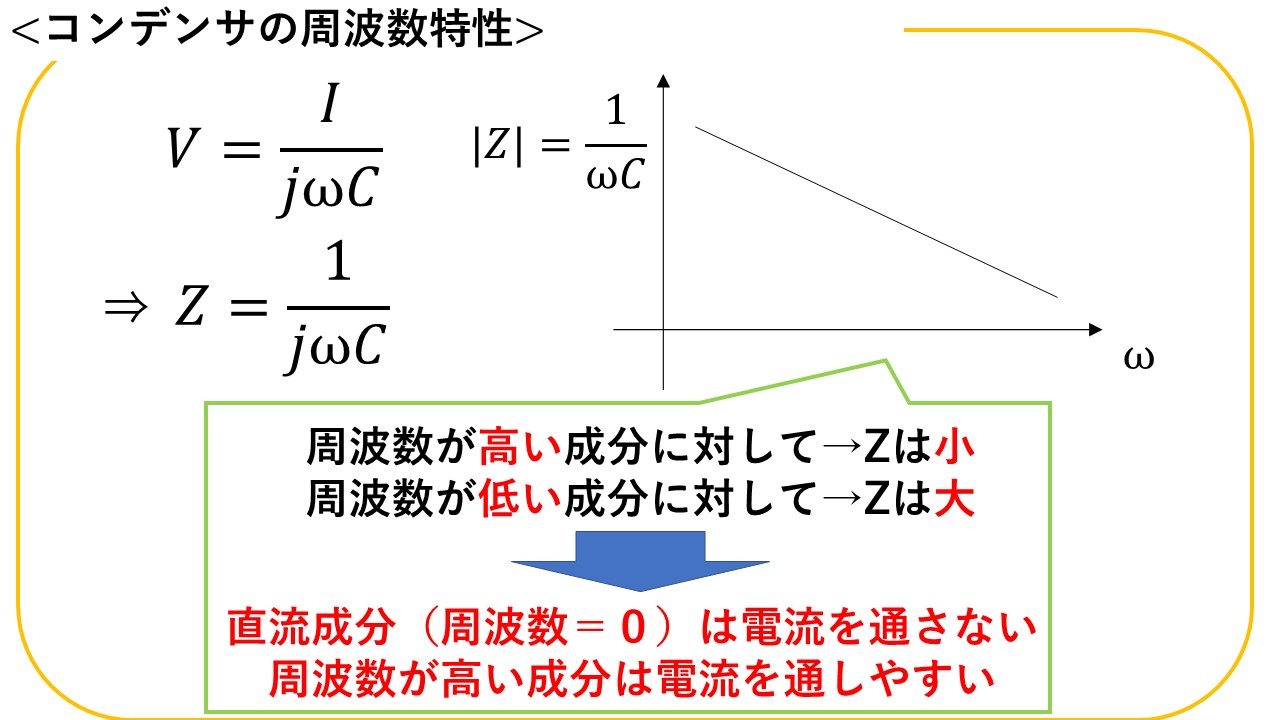
上記で説明したように，直流RC回路では定常状態でコンデンサに電流は流れません。言い換えれば，コンデンサは直流の電流を流さない性質があります！これについて，コンデンサの周波数特性から考えてみます！
コンデンサのインピーダンス|Z|は|Z|=1/(ωC)の形で求まります。ここで，ω=0，つまり直流の成分に対して考えると，|Z|=1/0≒∞となり，一切電流を流さない性質であることが分かります(^^)/ これが，直流RC回路で定常状態になるとコンデンサに電流が流れない理由になります(^^)/
なお，コンデンサには物凄い高い周波数の交流成分に対しては，非常に電流を通しやすい性質もありますので，ここで覚えておきましょう(^^)/
図10 コンデンサの周波数特性
時定数 ＝ 過渡現象の応答速度の指標
図8を見ると明らかなように，スイッチをONにした後の電荷q(t)は，いきなり定常値のCVになるのではなく，定常値に向けて徐々に変化していきます。この現象のことを過渡現象と呼び，電荷が定常値に向けて徐々に変化している状態を過渡状態と呼びます！ そして，この過渡現象の応答速度の指標となるのが，時定数τです(^^)/
時定数τとは，定常値のおよそ63%に到達するまでの時間のことで，RC回路ではτ=RCで求まります！
実際に，t=RCを代入すると，q(RC)=CV*(1-1/e)となり，1/eがおよそ0.37なので，q(RC)≒0.63*CVになります(^^)/ この時定数が短ければ，過渡現象はすぐに終わって，即座に定常値になります！ 一方で，時定数が長ければ，過渡状態は長くなり，なかなか定常値になりません！
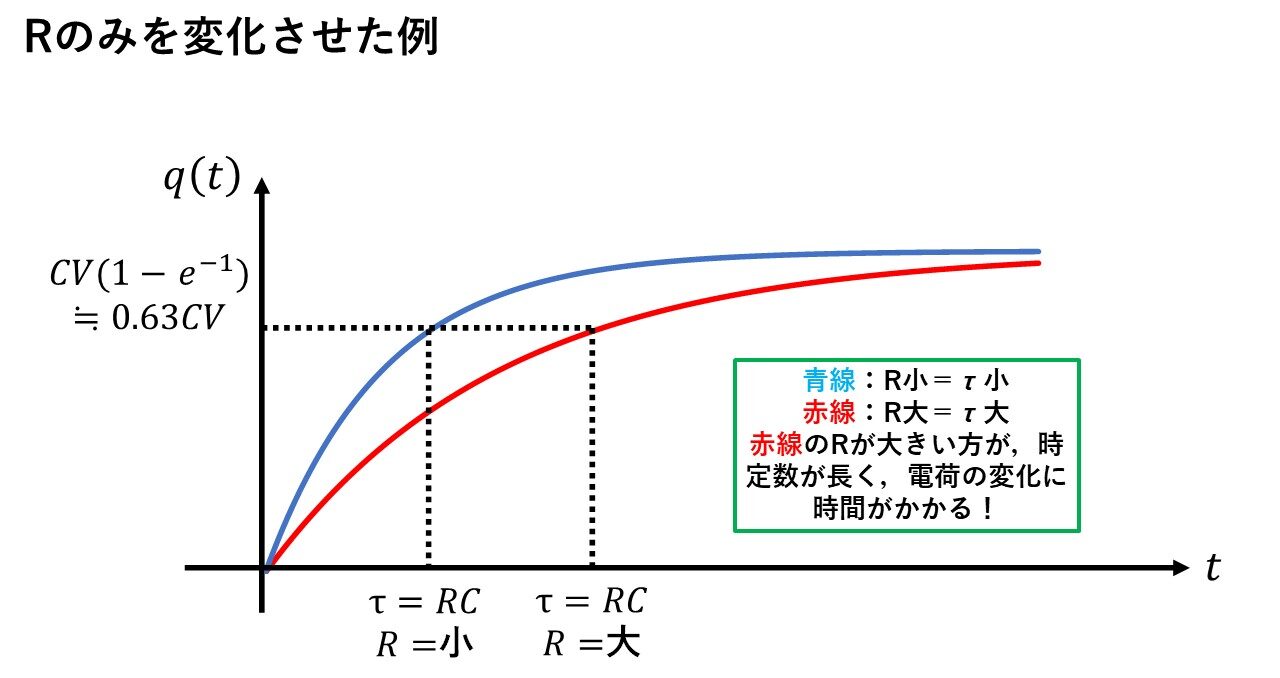
下のグラフは，Cの値を変えずに，Rだけを変えて時定数τを変えた例になります！Rが大きいほど，時定数τが長くなり，定常値に向けてゆっくりと変化しているのが分かりますね！
図11 時定数τ=RCを変化させた例 （Rのみを変更）
コンデンサに蓄積されるエネルギー
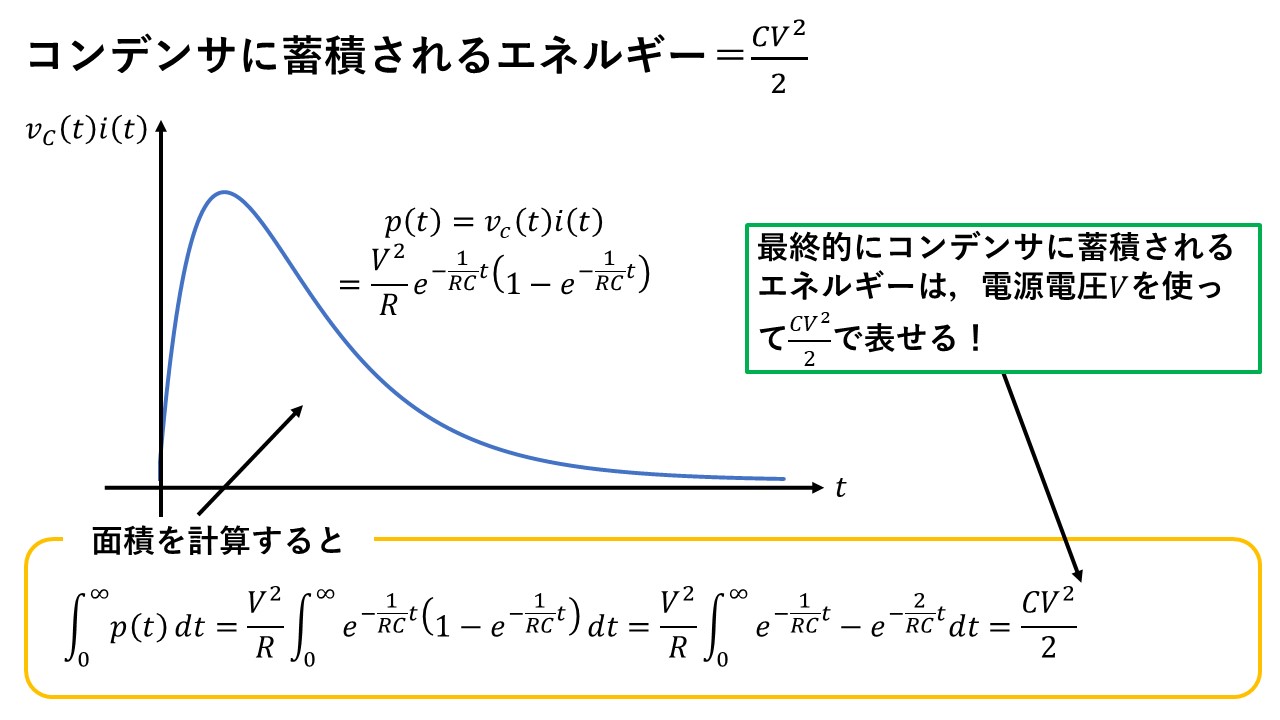
コンデンサに蓄積されるエネルギー=1/2*C*V^2とよく言いますが，この式はどこから出てくるのでしょうか？最後にこの式の出所を確認して，終わりましょう(^^)/
コンデンサに蓄積されるエネルギーは，ずばり瞬時電力p(t)(=コンデンサ電圧vc(t)×コンデンサを流れる電流i(t))を，スイッチを入れてから十分時間が経過する間で積分した値になります！つまり，瞬時電力のグラフの面積がコンデンサに蓄積されるエネルギーになります！実際に計算すると，電源電圧Vを使って，1/2*C*V^2という式になっているのが確認できますね！
図12 コンデンサに蓄積されるエネルギー
今回の記事はここまでです！この記事が，少しでも皆さんの役に立っていれば嬉しいです(^^)/
