こんにちは，ハヤシライスBLOGです！今回は直流RL回路を一階線形(非同次)微分方程式の解法を使って解いていきます！
直流RL回路
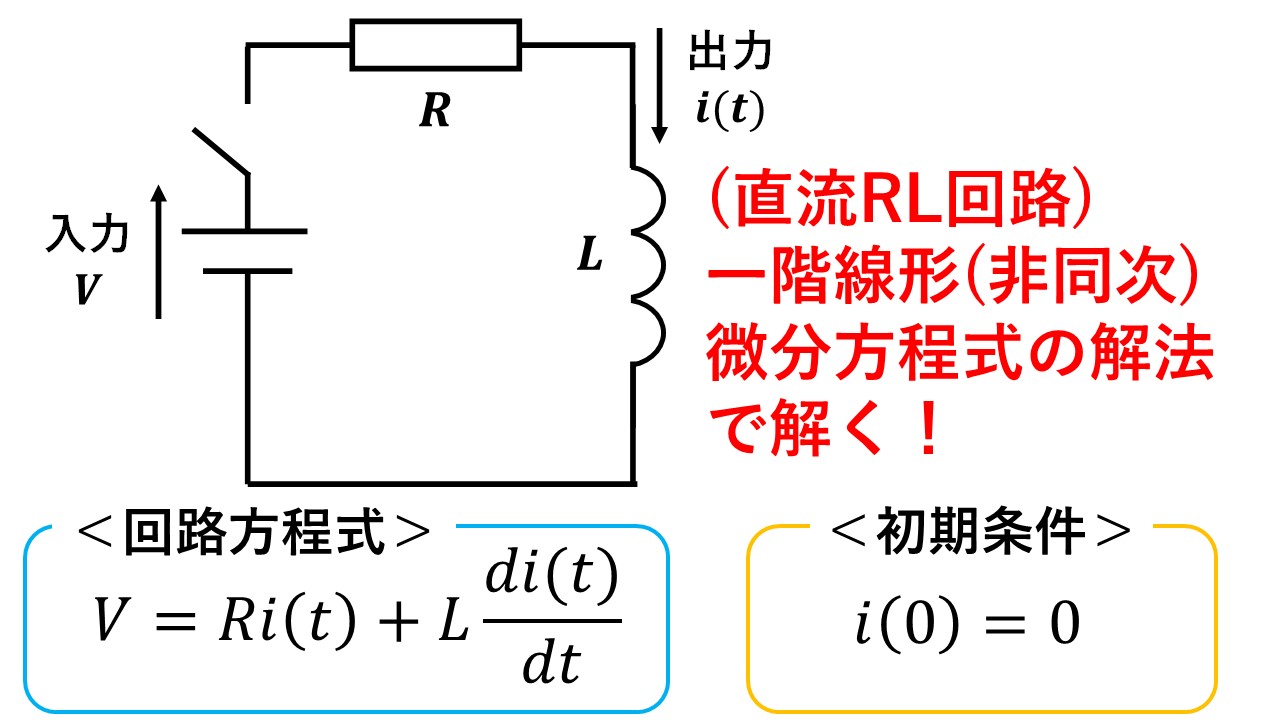
図1のようなRL回路に，時刻0[s]で直流電源をつないだ場合の応答を考えます！後程詳しく説明しますが，この回路の回路方程式は，一階線形(非同次)微分方程式と呼ばれる形になり，一般的な微分方程式の解法により解くことができます(^^)/ この記事では，解法のポイントや計算手順，RL回路の性質について解説します！
図1 直流RL回路
一階線形(非同次)微分方程式とは
一階線形(非同次)微分方程式とは，以下の図2の形で表される微分方程式のことです！q(x)≠0の場合を非同次方程式，=0の場合を同次方程式と呼びます(^^)/ この記事で扱う直流RL回路の方程式は，t=x，y=i，R/L=p(x)，V/L=q(x)と考えれば，一階線形(非同次)微分方程式になっていることが分かります！そのため，一般的な線形微分方程式の解法を使って，この回路の応答を計算していきます(^^)/
図2 一階線形(非同次)微分方程式とは
解法のポイント
ポイントは，
「非同次微分方程式の一般解＝①同次方程式の一般解＋②非同次方程式の特殊解」
になることです(^^)/ 要するに，①のV=0とした場合の一般解(任意定数を含んだ解)と，②の元々の回路方程式を満たす何か1つの解が分かれば，ほとんど計算終了ということです！
図3 解法のポイント
計算手順
一階線形(非同次)微分方程式の解法による直流RL回路の計算手順は以下の通りです！全部で4つのステップからなっています！ 1つずつ順番に解説していきます(^^)/
図4 計算手順
Step1：同次方程式の一般解を求めよう！
まず，回路方程式のV=0とした同次方程式の一般解を求めていきます！同次方程式が変数分離系の形になっているので，左辺を電流iの関数，右辺を時間tの関数に分けて積分することで，以下のように簡単に同次方程式の一般解を計算できます(^^)/
また，一般解と聞くと何か難しそうな感じがしますが，要するに解の中に任意定数を含んだものが一般解と考えてもらえればいいと思います！c2=10の場合でも，c2=1の場合でも，どちらもこの同次方程式の解であるように，解の形が□*e-(-R/L*t)になっていれば，この同次方程式を満たす解は無数にあって，ただ一つの解に限定できないので一般解というわけですね！
図5 同次方程式一般解の求め方
Step2：非同次方程式の特殊解を求めよう！
続いて，非同次方程式の特殊解を求めます！特殊解というのは，少なくともその方程式の解にはなっているが，その方程式を満たす一般的な解の形にはなっていない，そんな解が特殊解です！つまり，何か一つでもある方程式を満たす解が見つかればそれが特殊解になります(^^)/
ではどうやって特殊解を求めましょうか？何でもいいので何か一つと言われても，実際に求めようとすると困りますよね？そんな時は，定常状態，つまり，スイッチがONになってから十分に時間が経った場合を考えてください！すると，後程ご説明しますが，コイルは十分時間が経った場合は短絡状態，つまり，コイルの起電力L*di/dt=0とみなせますから(※)，簡単に特殊解i2(t)=V/Rと求めることができます(^^)/
※）十分時間が経った後を考えれば，いつもコイルの起電力L*di/dt=0となるわけではありません。ここでは，直流電源をつないだ場合を考えているので問題ありませんが，交流の電源をつないだ場合は，電流の方向が＋と－で行ったり来たりするので，いつまで経ってもコイルに発生する起電力はなくならず，L*di/dt=0とみなすことはできません！
図6 非同次方程式特殊解の求め方
念のため，i2(t)=V/Rが本当に非同次方程式の解になっているかは，元の式に代入して確認するようにしましょう！ 以下の通り，ちゃんと解になっていますね(^^)/
図7 i2(t)=V/Rが非同次方程式特殊解になっているかの確認
Step3：非同次方程式の一般解を求めよう！
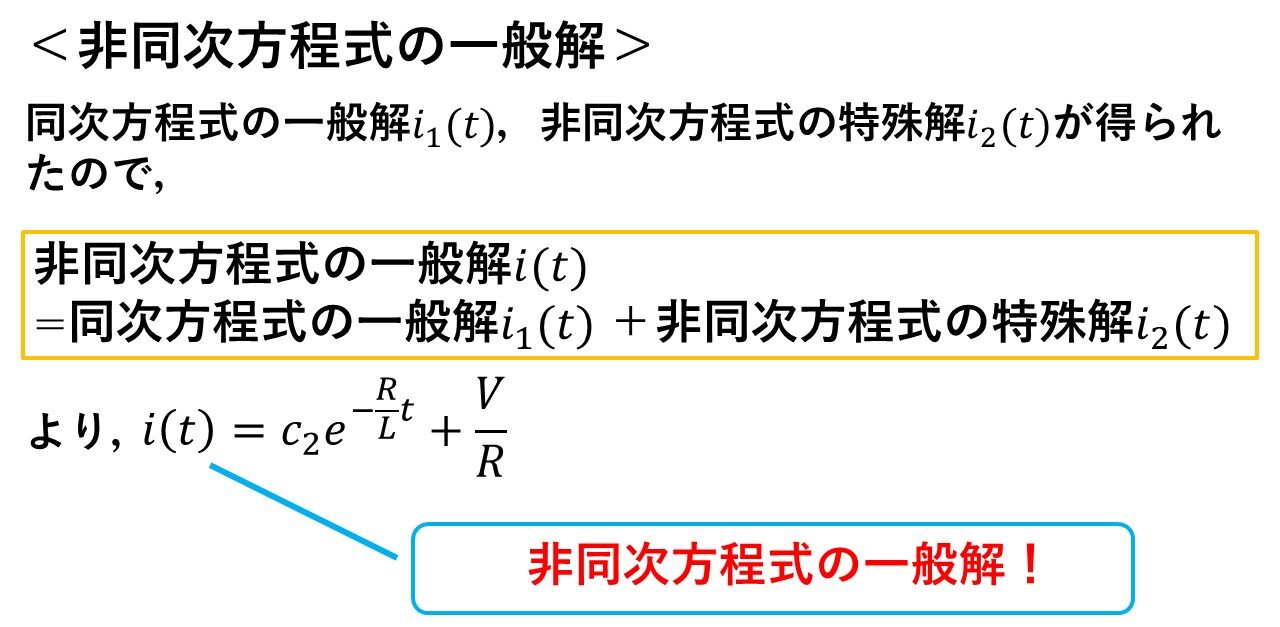
Step1で同次方程式の一般解i1(t)が求まり，Step2で非同次方程式の特殊解i2(t)が求まったので，非同次方程式の一般解は，これらを足して以下のように求まります！
図8 回路方程式の一般解
Step4：回路の初期条件から任意定数を求めよう！
最後に，今回求められている解は，あくまで回路の初期条件「t=0の時の電流が0」を満たす解です！そのため，Step3で求めた一般解のうち，この条件を満たす解を求める必要があります！
つまり，時刻0[s]の時の電流が0になるような任意定数を求めればよいので，以下のように簡単に求めることができます(^^)/ これで，最終的な解が求まりましたね！
図9 最終的な解
直流RL回路の特徴
さて，直流RL回路の解法が分かったので，今度はその回路の特徴や性質についておさえましょう(^^)/
コイルの性質
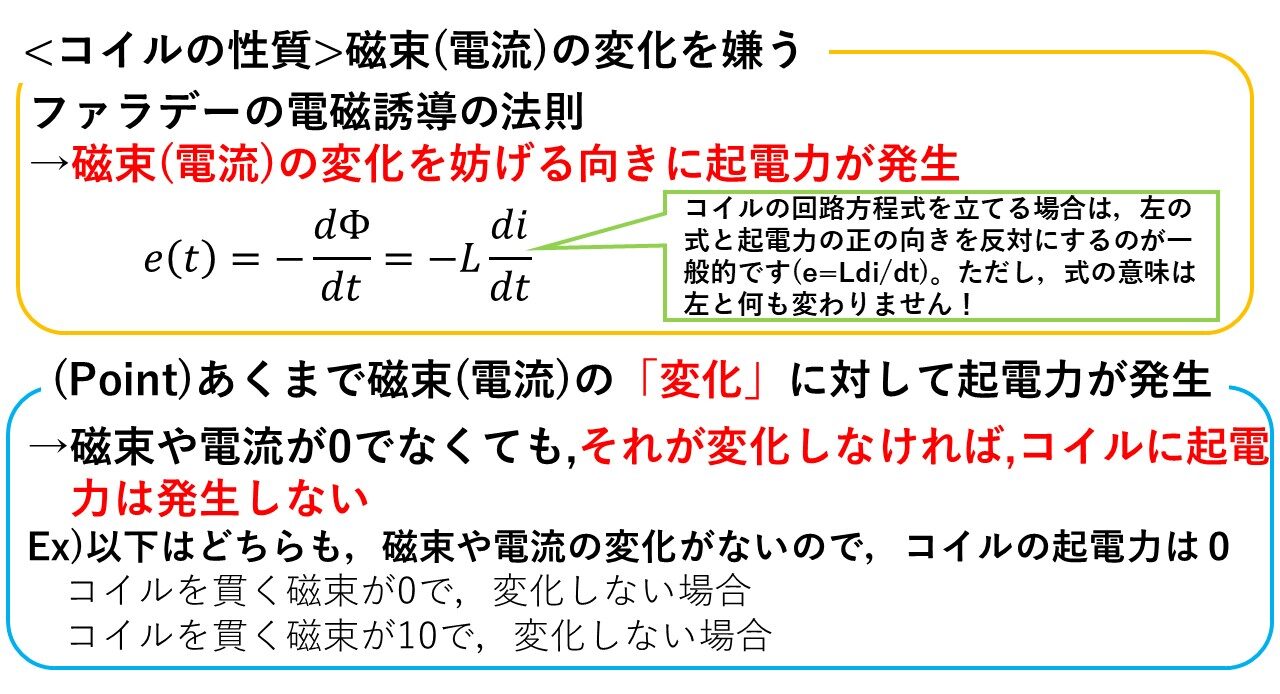
ポイントは，ずばりコイルの性質です！ コイルは，磁束の変化を嫌います。Φ=LIの式からも明らかなように，磁束は電流によって作られるので，結果的にコイルは電流の変化を嫌います！これは，ファラデーの電磁誘導の法則の式からも明らかで，コイルは磁束(電流)の変化を妨げる向きに起電力を発生し，なんとか磁束(電流)が変化するのを阻止しようとします(^^)/※
気を付けて欲しいのは，コイルはあくまでも磁束(電流)の「変化」を嫌うということです！ 要するに，磁束や電流が変化する瞬間には，コイルは起電力を発生させて，磁束や電流が変化するのを思いっきり邪魔しようとしますが，一度変化して十分時間が経った後では，実際に磁束や電流が発生していても．コイルは起電力を発生させず，短絡状態となり一切邪魔はしません！
※)細かい点ですが，回路方程式を立てる時，一般的にコイルの起電力に－はつけません。これは，逆起電力と呼ばれて，あらかじめコイルの起電力の正の向きを，ファラデーの電磁誘導の法則と反対に定義しているからです。しかし，磁束(電流)の変化を妨げる向きに起電力を発生させるという本質は何も変わっていませんので，注意しましょう(^^)/
図10 コイルの性質
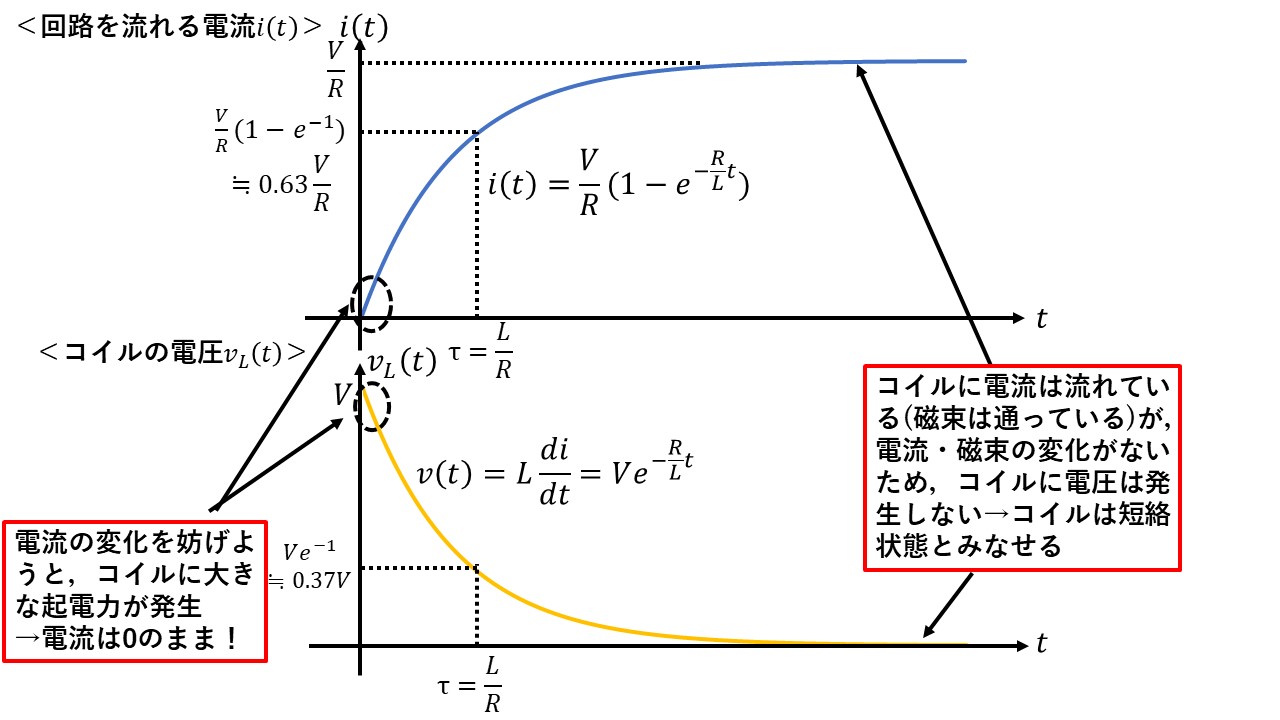
実際に直流RL回路の電流およびコイルの電圧のグラフを見てみましょう！スイッチをONにした直後と，スイッチをONにしてから十分時間が経った後を見ると，以下のようにこれまで述べてきたコイルの性質を確認することができます(^^)/
スイッチをONにした直後）
スイッチON直後には，コイルの磁束(電流)の変化を嫌う性質により，コイルには電流の変化を妨げる方向に大きな起電力が発生し(下図)，実際に電流は即座に変化しません（上図）！
スイッチをONにしてから十分時間が経った後）
スイッチをONにして十分時間が経った後では，コイルに電流が流れていても(上図)，コイルに起電力は発生せず，短絡状態となります(下図)！
図11 直流RL回路の電流とコイルの電圧
時定数 ＝ 過渡現象の応答速度の指標
図11を見ると明らかなように，スイッチをONにした後の電流i(t)は，いきなり定常値のV/Rになるのではなく，定常値に向けて徐々に変化していきます。この現象のことを過渡現象と呼び，電流が定常値に向けて徐々に変化している状態を過渡状態と呼びます！ そして，この過渡現象の応答速度の指標となるのが，時定数τです(^^)/
時定数τとは，定常値のおよそ63%に到達するまでの時間のことで，RL回路ではτ=L/Rで求まります！
実際に，t=L/Rを代入すると，i(L/R)=V/R*(1-1/e)となり，1/eがおよそ0.37なので，i(L/R)≒0.63*V/Rになります(^^)/ この時定数が短ければ，過渡現象はすぐに終わって，即座に定常値になります！ 一方で，時定数が長ければ，過渡状態は長くなり，なかなか定常値になりません！
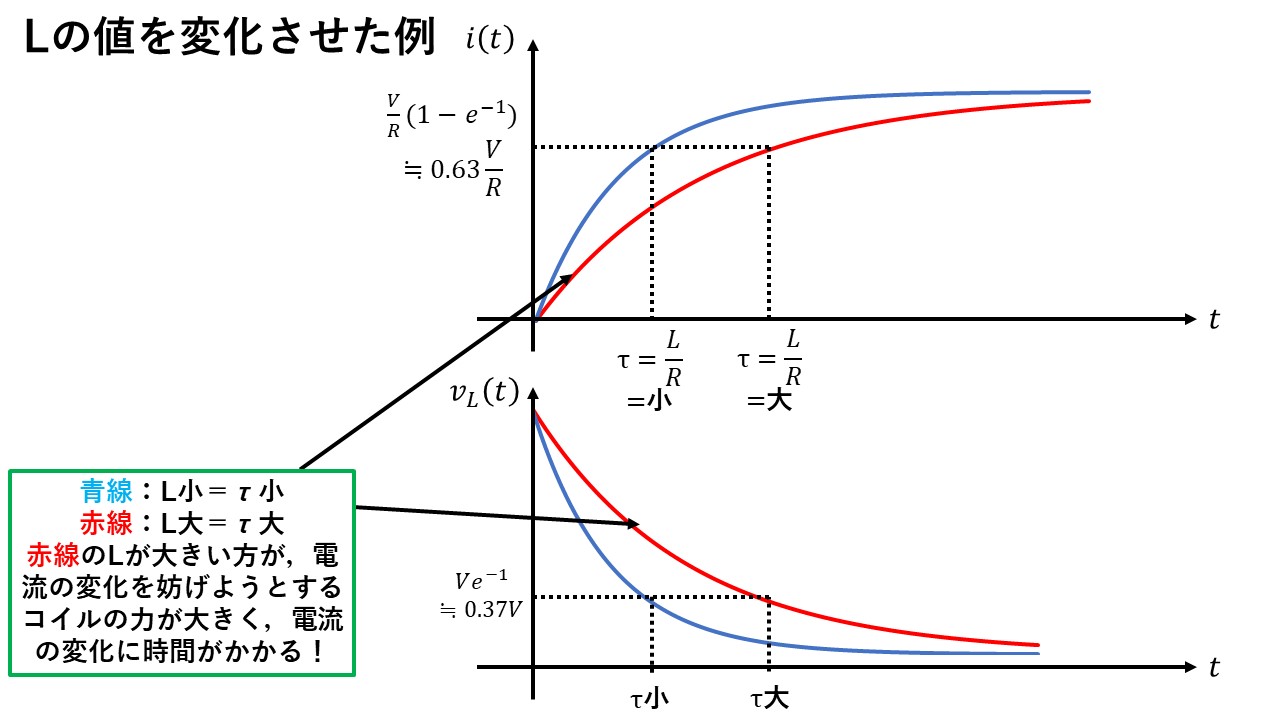
下のグラフは，Rの値を変えずに，Lだけを変えて時定数τを変えた例になります！Lが大きいほど，時定数τが長くなり，定常値に向けてゆっくりと変化しているのが分かりますね！コイルのLが大きくなって，電流の変化を妨げる力が強くなったので，電流の変化がゆっくりになったわけですね(^^)/
図12 時定数τ=L/Rを変化させた例
コイルに蓄積されるエネルギー
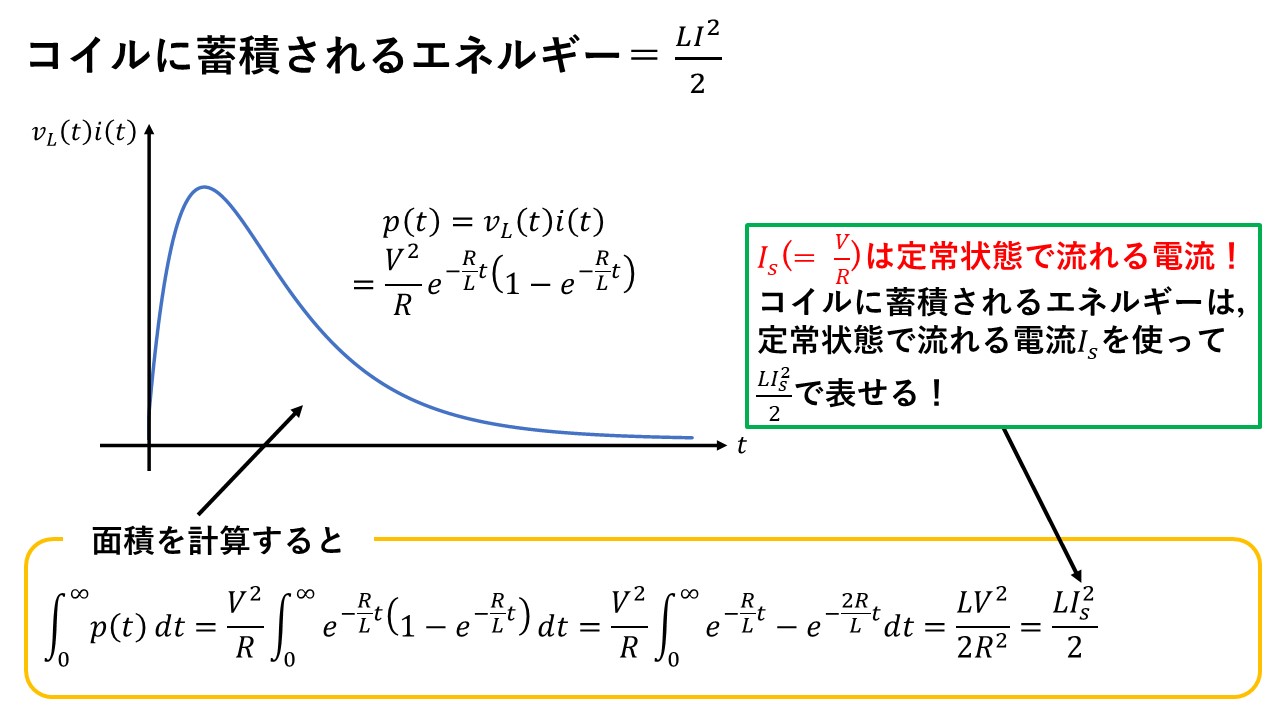
コイルに蓄積されるエネルギー=1/2*L*I^2とよく言いますが，この式はどこから出てくるのでしょうか？最後にこの式の出所を確認して，終わりましょう(^^)/
コイルに蓄積されるエネルギーは，ずばり瞬時電力p(t)(=コイルの起電力vL(t)×コイルを流れる電流i(t))を，スイッチを入れてから十分時間が経過する間で積分した値になります！つまり，瞬時電力のグラフの面積がコイルに蓄積されるエネルギーになります！実際に計算すると，電流の定常値Isを使って，1/2*L*Is^2という式になっているのが確認できますね！
図13 コイルに蓄積されるエネルギー
今回の記事はここまでです！この記事が，少しでも皆さんの役に立っていれば嬉しいです(^^)/
