こんにちは，ハヤシライスBLOGです！今回は誘導機の等価回路についてできるだけ分かりやすく解説します。
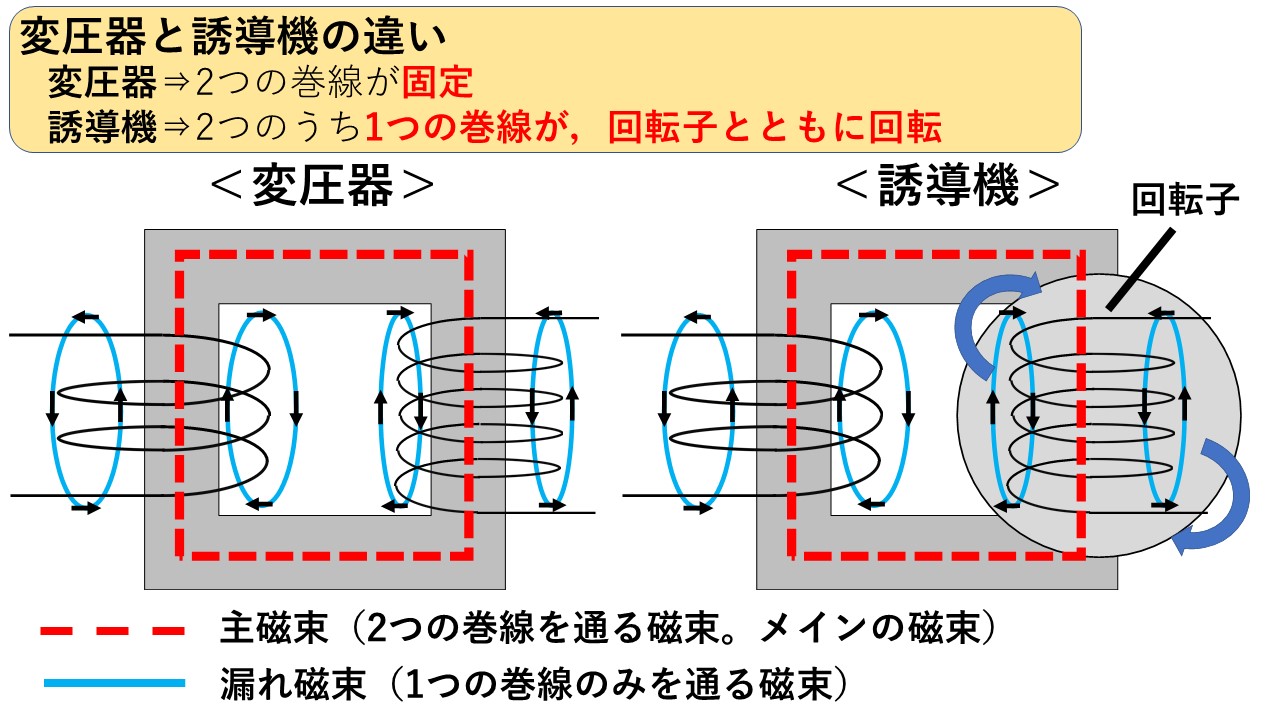
変圧器と誘導機の違い
図1の通り，変圧器も誘導機も基本的な構造は同じで，違いは変圧器の場合は2つの巻線が固定されているのに対し，誘導機では回転子巻線が回転子と一緒に回転しているという点のみです(^^)/
図1 変圧器と誘導機の違い
ここで，変圧器や誘導機に登場する磁束は，以下の2つに分けられます(^^)/ 主磁束も漏れ磁束もどちらも磁束ですが，磁束ではなく電圧で考える電気回路上では，それぞれの表現は違いました！変圧器の記事がまだの方は，以下の変圧器の記事を是非読んでみてください(^^)/
・主磁束
⇒2つの巻線を通る磁束。メインの磁束。変圧器の等価回路では，理想変圧器としてあらわされる
・漏れ磁束
⇒それぞれの巻線のみを通る磁束。変圧器の等価回路では，漏れインピーダンスとしてあらわされる
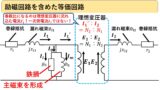
それでは誘導機と変圧器の構造上の違いによって，主磁束と漏れ磁束の等価回路がどう変わるのか，順番に見ていきましょう！
主磁束の等価回路について
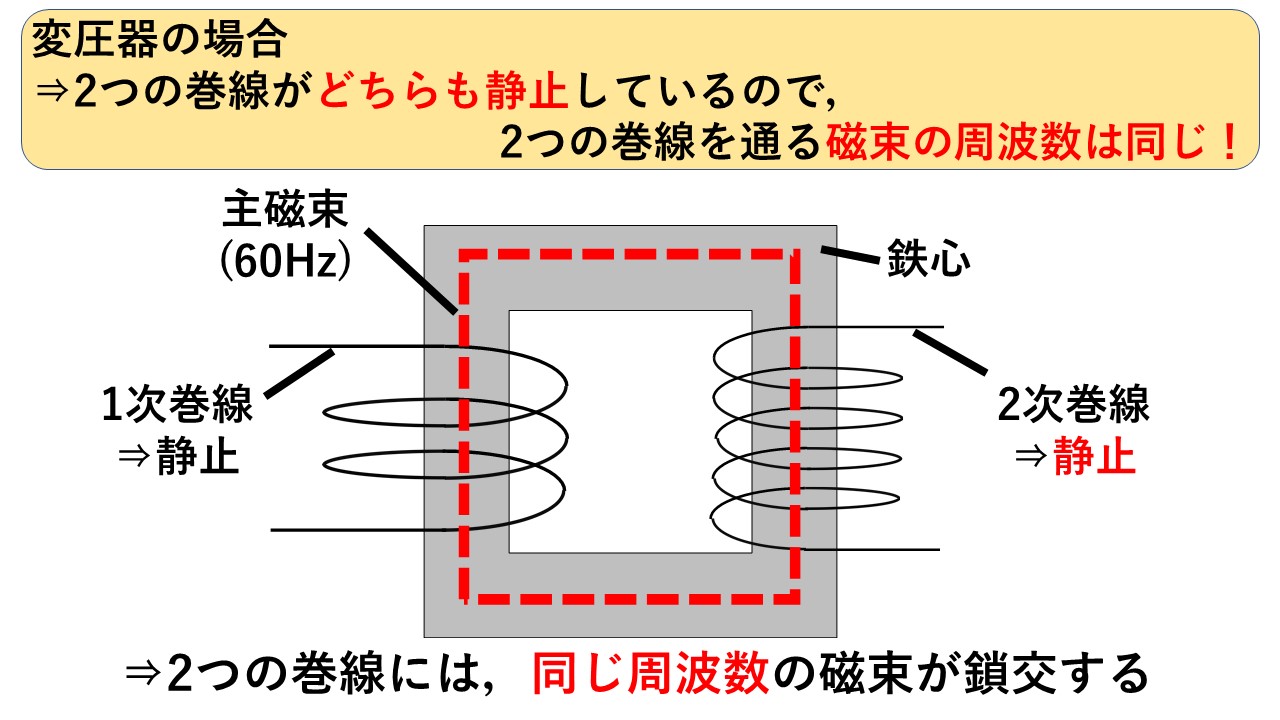
変圧器の場合（復習）
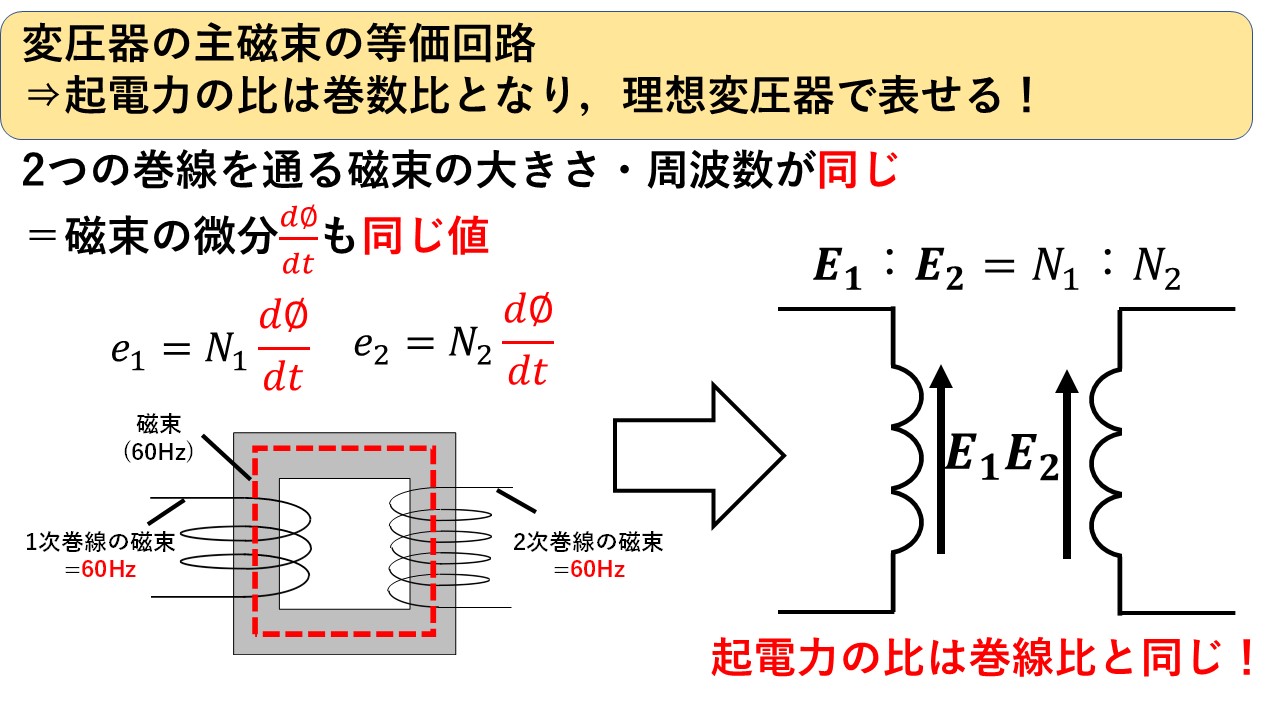
図2は，変圧器の主磁束に関する図になります。変圧器の場合，2つの巻線が静止しているため，例えば60Hzの電源を変圧器につなげば，2つの巻線にはともに60Hzの磁束が鎖交します！したがって，図3の通り，2つの巻線を通る磁束の大きさ・周波数が同じなので，当然その変化の仕方(=dφ/dt)も同じになるので，起電力の比は巻線比となり，理想変圧器で表すことができます！
図2 変圧器の主磁束
図3 変圧器の主磁束に関する等価回路
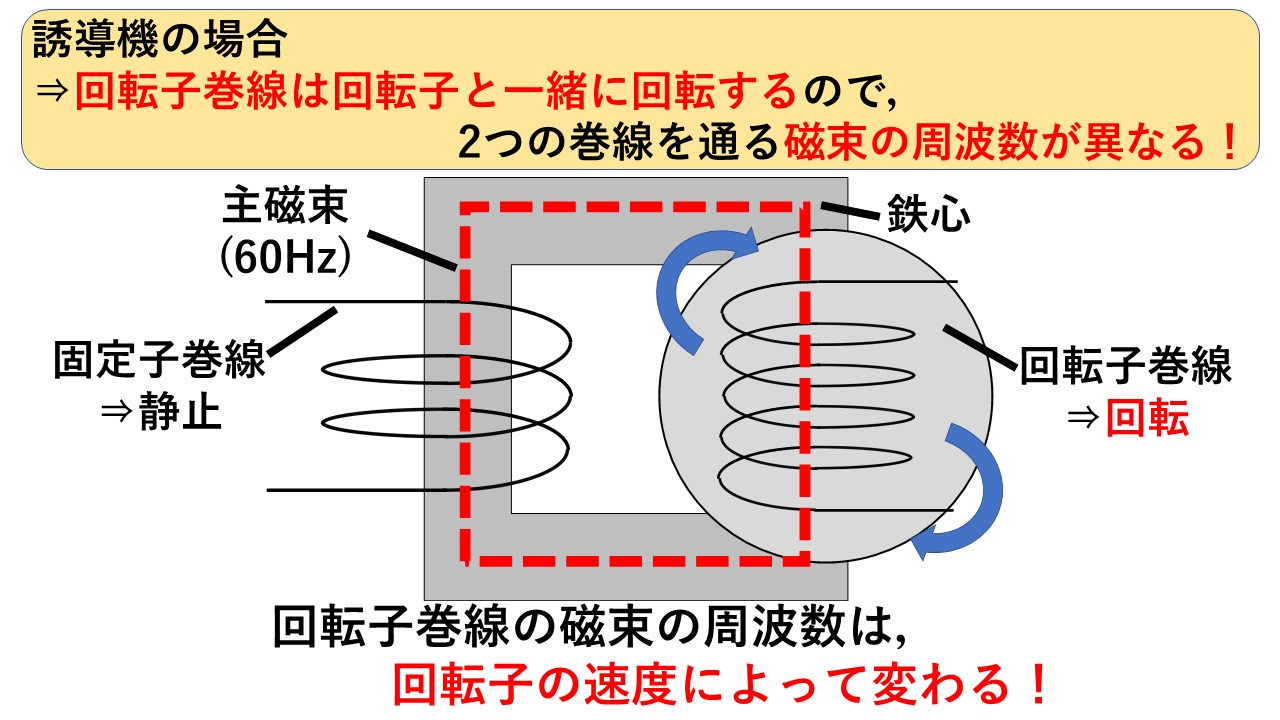
誘導機の場合
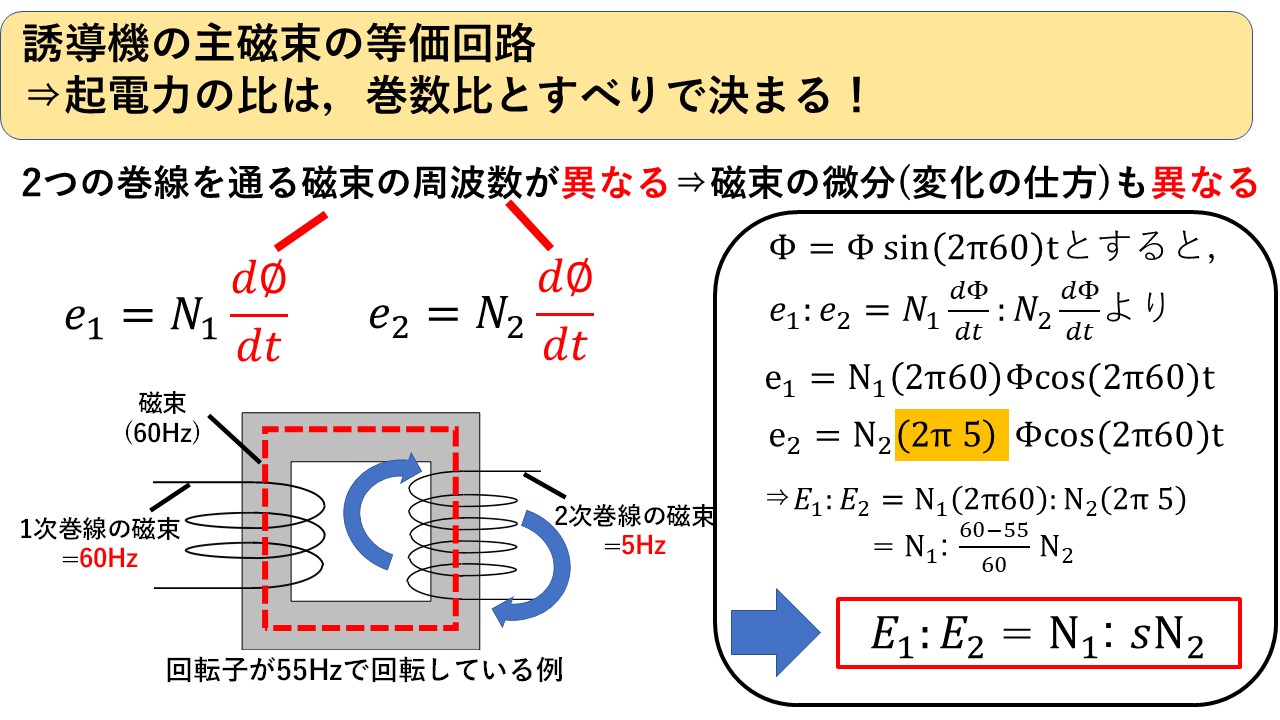
一方で，誘導機の場合は，図4のように固定子巻線を通る磁束の周波数は常に60Hzであるのに対し，回転子巻線は回転子と一緒に回転しているため，巻線を通る磁束の周波数が回転子の速度によって変化し，固定子と回転子では巻線を通る磁束の周波数が違います！
イメージが湧かないかもしれないので，以下で3つの例を見てみましょう！
図4 誘導機の主磁束
回転子が静止している場合
図5のように，回転子の速度が0場合，固定子が作る回転磁界が60Hzで回るとすると，止まっている回転子からすれば，回転磁界は60Hzで回ってみえるので，回転子には60Hzの磁束が通ります！これはまさに，変圧器と同じ状況ですね！
図5 誘導機主磁束の回転子への伝わり方（回転子=静止の場合）
回転子が55Hzで回転している場合
図6のように，回転子の速度が55回転/sの場合，回転子からすれば，回転磁界は自分よりちょっとだけ早く見えて，1秒間に5回転して見えます！そのため，回転子を通る磁束の周波数は5Hzになります(^^)/
60m/sで走る電車を止まった所からみると，60m/sで動いて見えますが（回転子=静止の場合に対応），自分も55m/sで走る電車に乗れば，その電車は5m/sで進んで見えますよね！（回転子=55Hzの場合に対応）
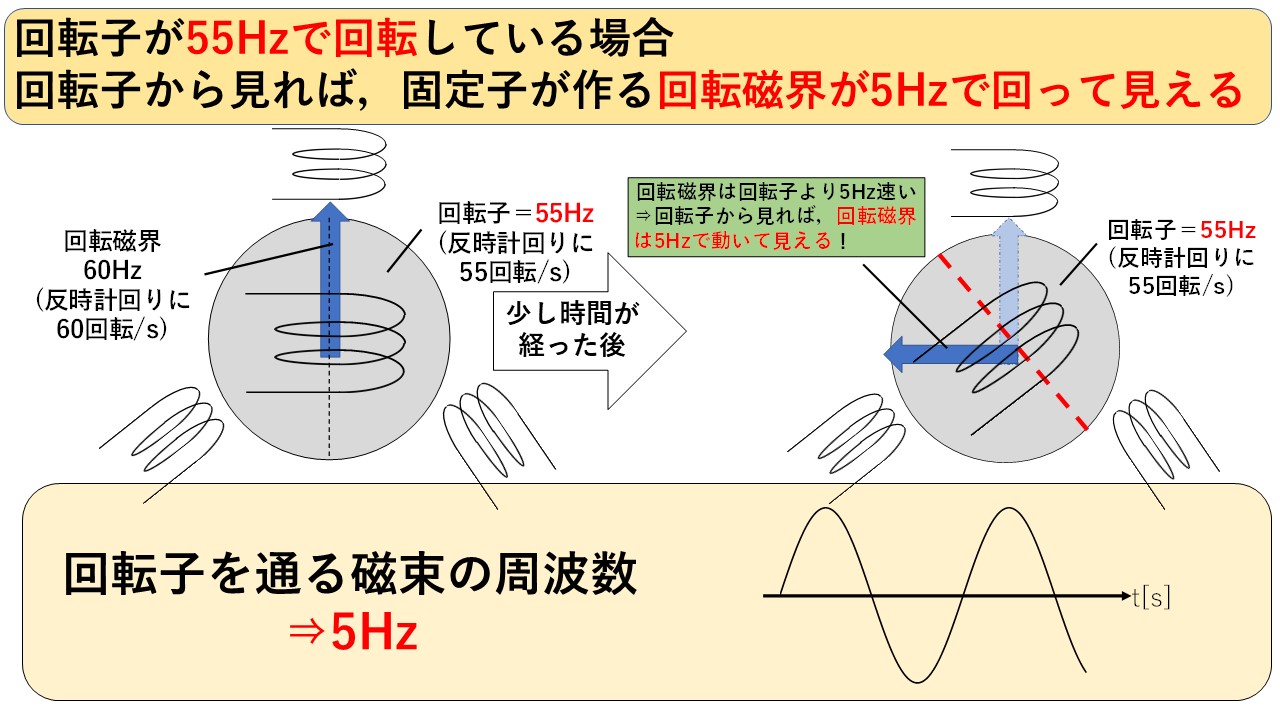図6 誘導機主磁束の回転子への伝わり方（回転子=55Hzの場合）
回転子が60Hzで回転している場合
図7のように，回転子の速度が60回転/sの場合，回転磁界と回転子の速度は同じなので，回転子からすれば，回転磁界は止まって見えます！そのため，回転子を通る磁束の周波数は0Hzになります(^^)/
60m/sで走る電車を，60m/sで走る電車から見れば，止まって見えますよね(^^)/
図7 誘導機主磁束の回転子への伝わり方（回転子=60Hzの場合）
以上から，誘導機の場合，回転子巻線を通る主磁束の周波数は回転子の速度によって変わるため，2つの巻線を通る磁束の周波数が違ってくるというのが分かったかと思います！したがって，誘導機の主磁束を電圧で考えると，図8のように，2つの巻線を通る磁束の周波数が異なるため，dφ/dtの大きさが異なり，起電力の比は巻線の比とすべりの比によって変わります(^^)/
図8 誘導機の主磁束に関する等価回路
漏れ磁束の等価回路について
変圧器の場合（復習）
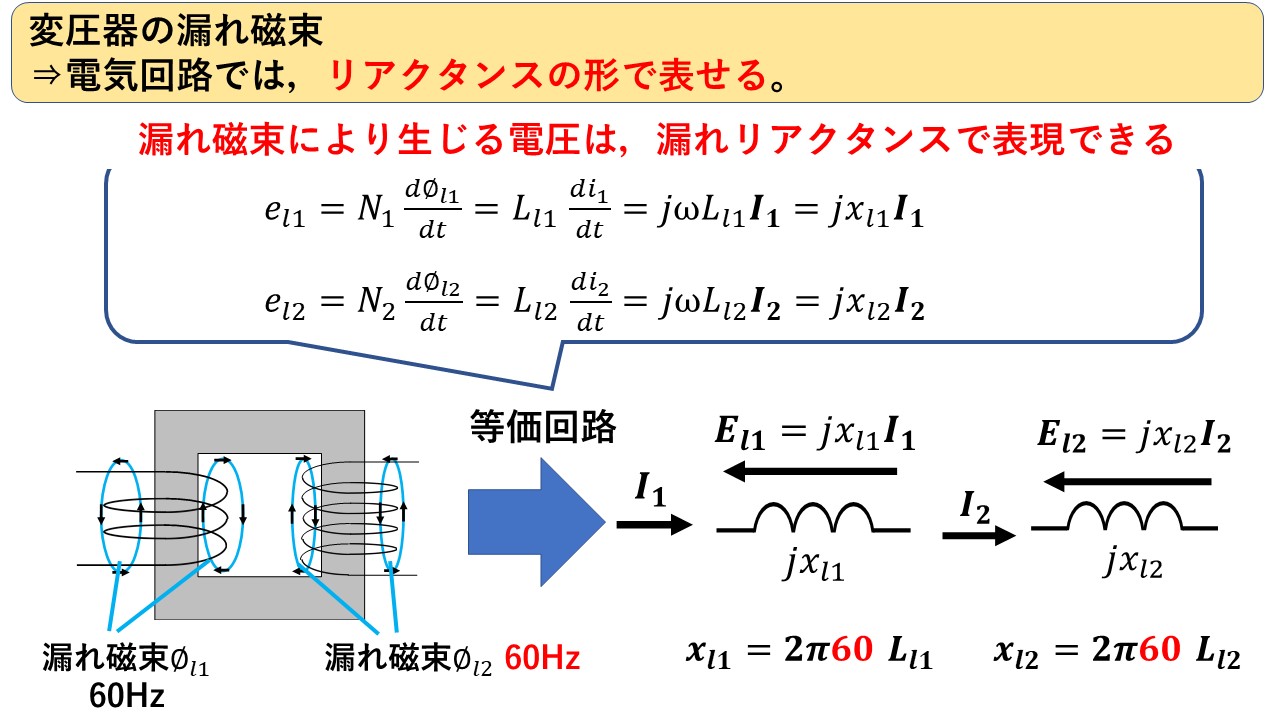
図9は，変圧器の漏れ磁束に関する図になります。漏れ磁束により生じる電圧は，等価回路上ではリアクタンスの形で表せます！
図9 変圧器の漏れ磁束に関する等価回路
誘導機の場合
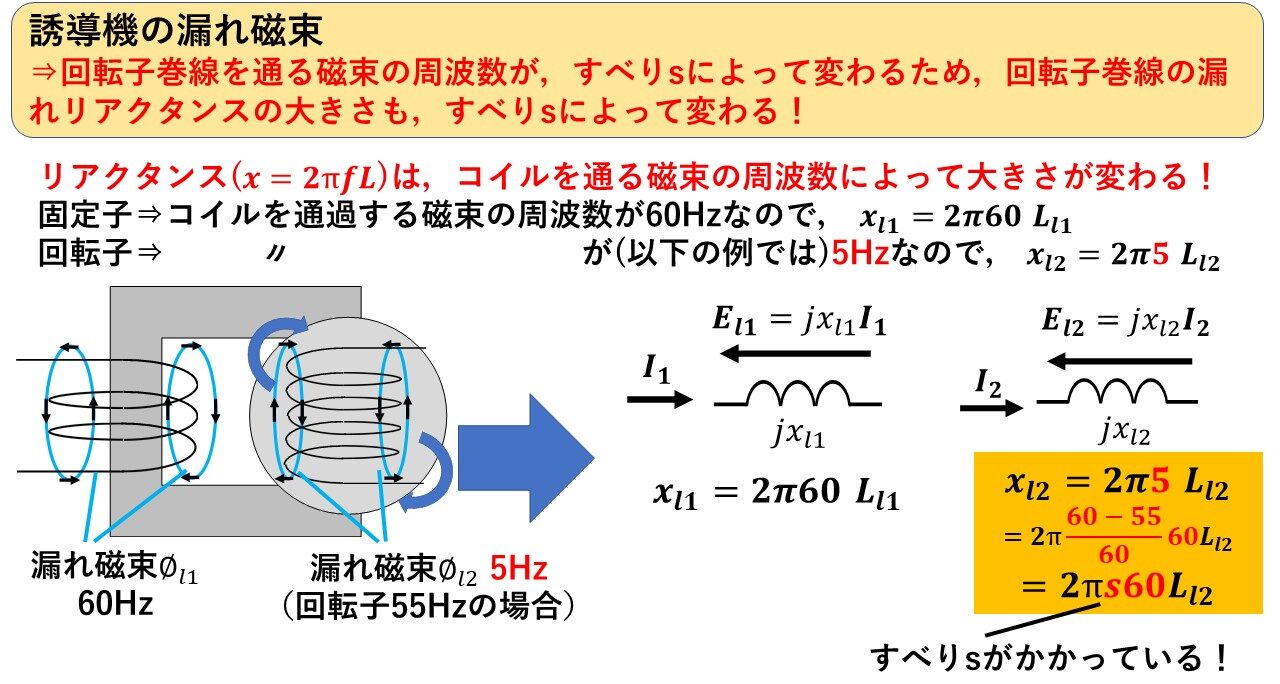
図10は，誘導機の漏れ磁束に関する等価回路になります！ここで重要なのは，そもそもリアクタンスは，2πLで表されることからも分かるように，コイルを通る磁束の周波数によってその大きさが変化します！変圧器の場合は，2つのコイルを通る磁束の周波数はどちらも同じ(この記事の例では60Hz)でしたが，誘導機の場合は回転子のコイルを通る磁束の周波数は，すべりsによって変わる（この記事の例では5Hz)ため，回転子の漏れリアクタンスはすべりsによって変わります！
図10 誘導機の漏れ磁束に関する等価回路
誘導機と変圧器の等価回路の違い
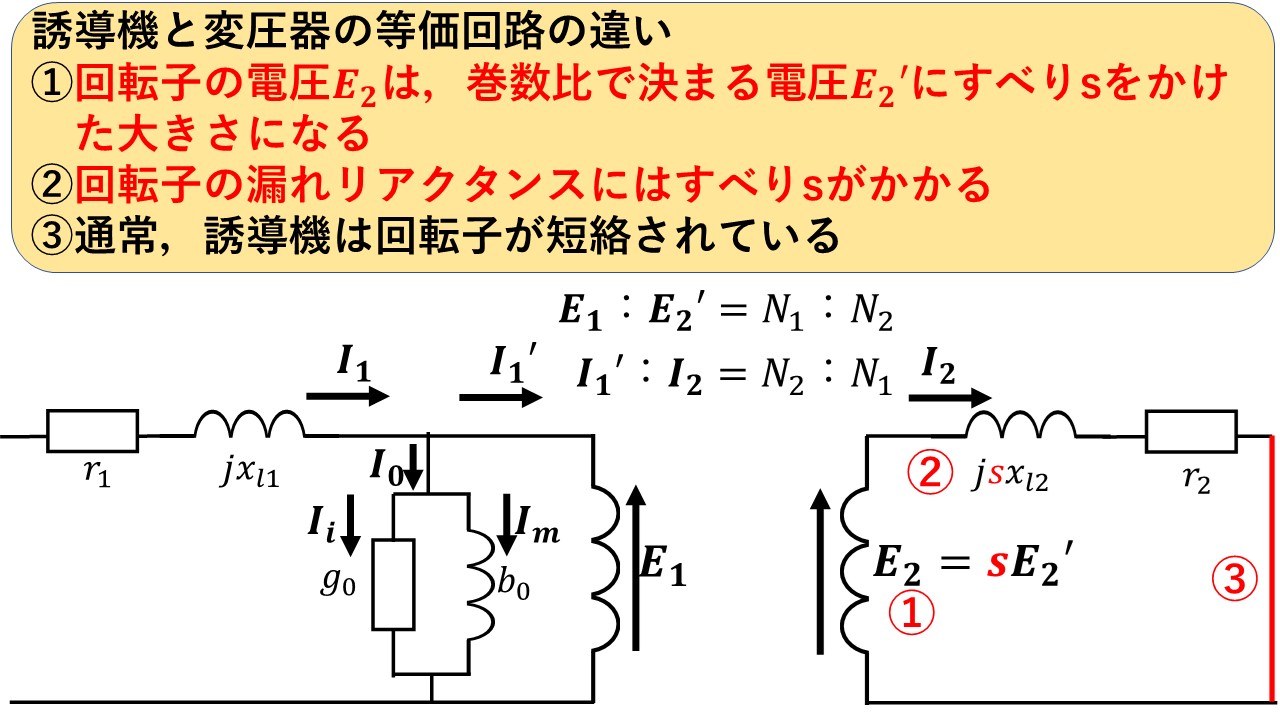
これまでの説明をまとめると，誘導機と変圧器の等価回路の違いは図11のようにまとめることができます！これまでの主磁束に関する説明が①，漏れ磁束に関する説明が②に対応しています(^^)/ なお，説明を省いてきましたが，③にあるように，誘導機の回転子巻線は通常短絡されています！，
図11 誘導機と変圧器の等価回路の違い
固定子側換算の誘導機等価回路の導出
最後に，固定子側に換算した誘導機の等価回路を導出して終わります！ 変圧器でも1次側に換算した等価回路を導出しますよね？ それの誘導機バージョンです(^^)/
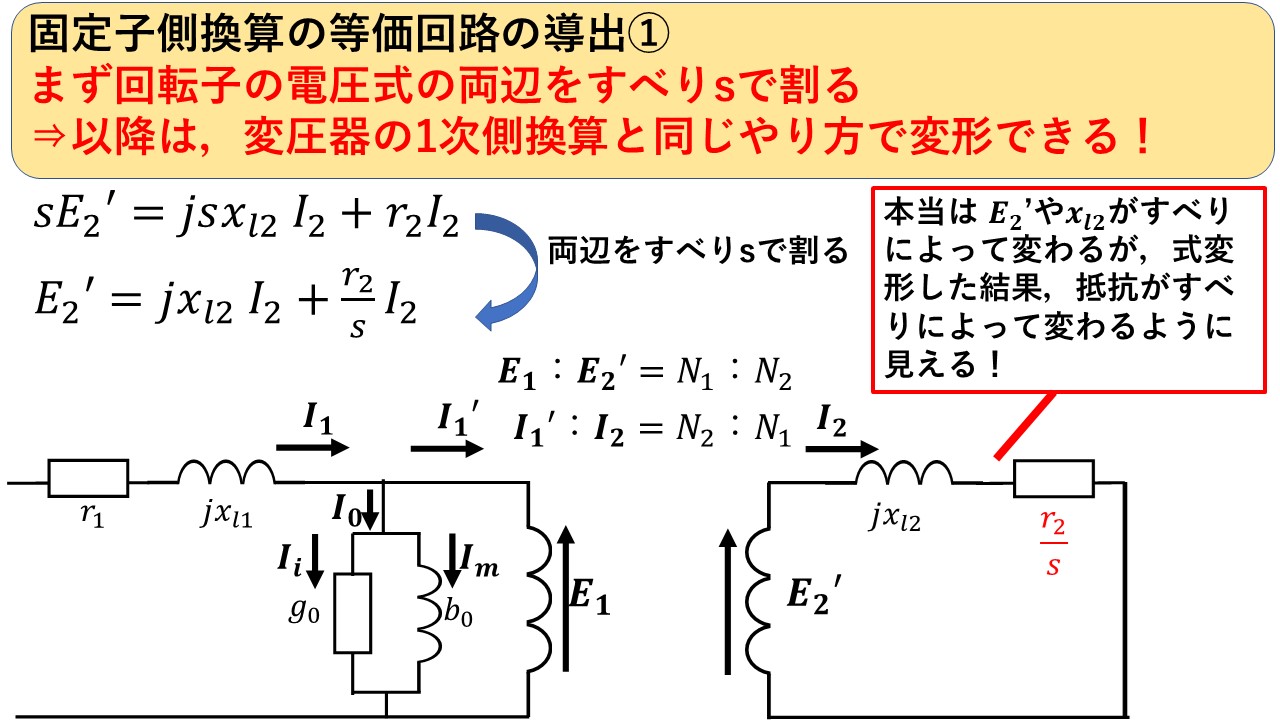
固定子側に換算した誘導機の等価回路を導出する際のポイントはだた一つです！それは，図12のように，回転子の電圧式の両辺をすべりで割るということです！この理由は，回転子の電圧式をすべりで割ることによって，回転子に生じる起電力がsE2’からE2’に変わることで，すべりsがなくなり，後は変圧器と同様のやり方で固定子側に換算できるからです(^^)/ 当然ですが，単に式変形しただけなので，単に見栄えが変わっただけで式の持つ意味は何も変わりません！ 注意点としては，本当はすべりによって変わるのは起電力E2’や漏れリアクタンスxl2なのですが，式変形したことで，抵抗がすべりによって変わるように見えます！
図12 固定子側換算の誘導機等価回路の導出（step1)
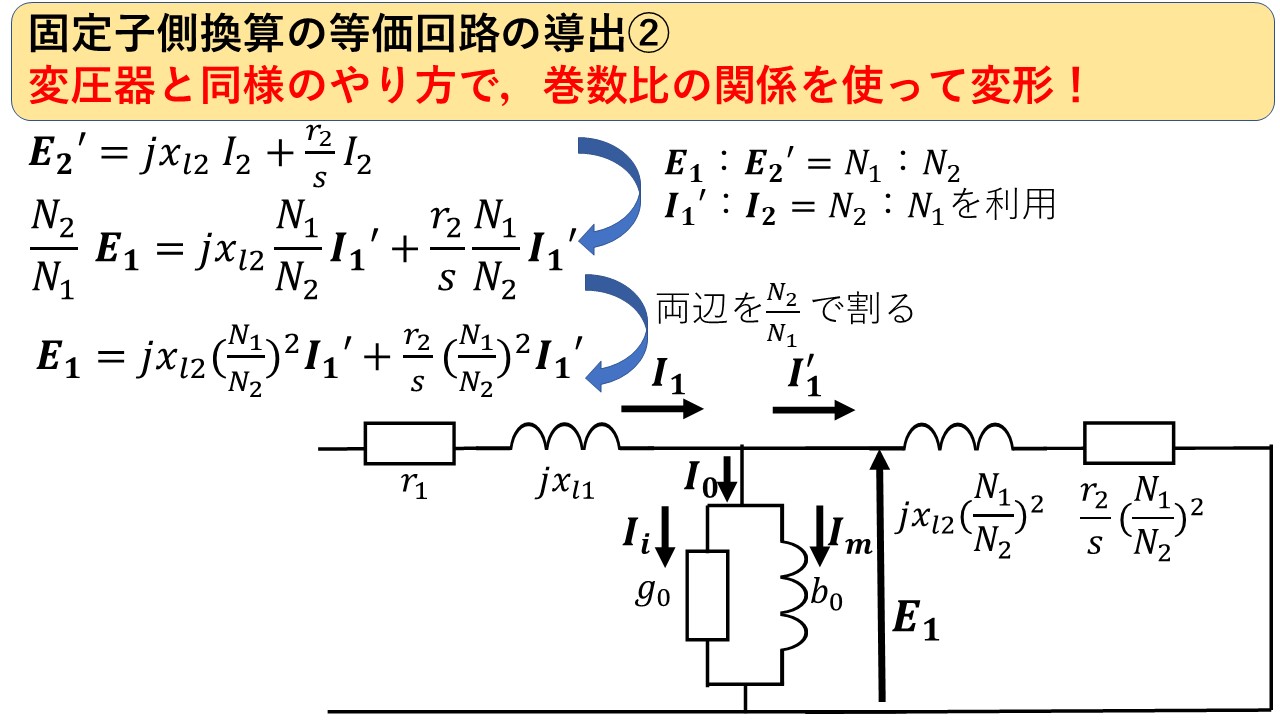
後は，図13のように，変圧器の1次側換算と同様のやり方で巻数比を考慮しながら換算すれば，最終的に固定子側換算の誘導機等価回路を導出することができます(^^)/
図13 固定子側換算の誘導機等価回路の導出（step2)
以上，誘導機の等価回路についてでした！お疲れ様でした(^^)/
