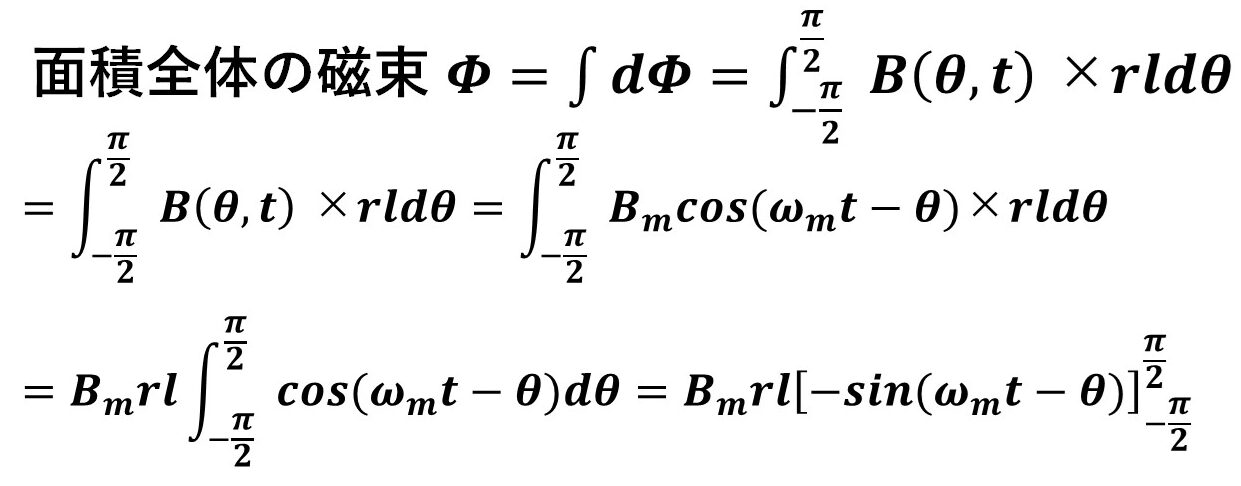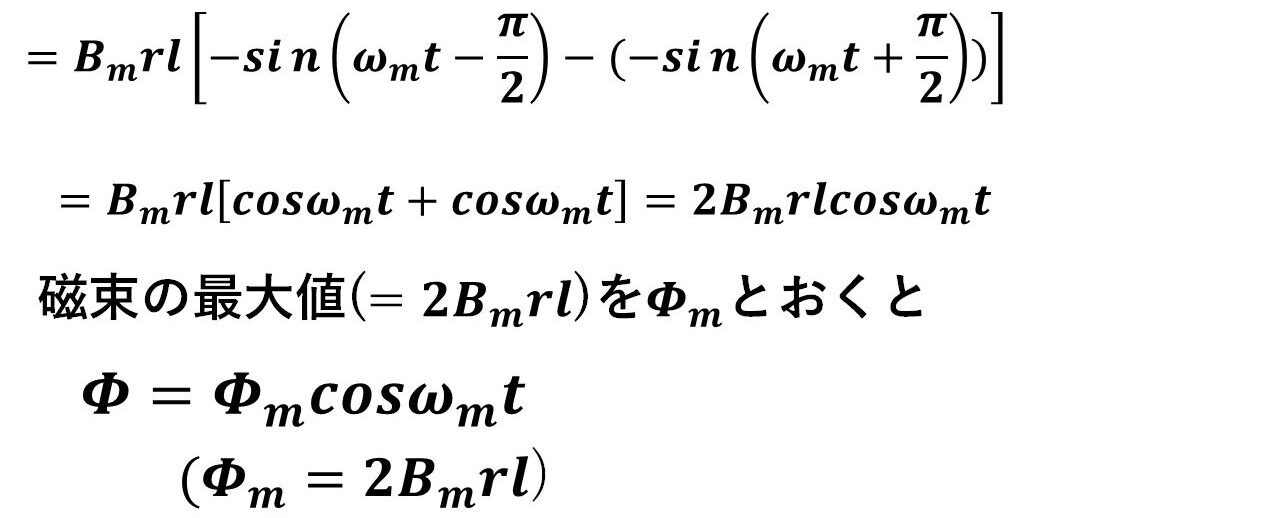こんにちは，ハヤシライスBLOGです！今回は，同期発電機の誘導起電力の公式を分かりやすく解説します(^^)/ 具体的には，語呂を使った公式の覚え方や，公式の導出過程を紹介しておりますので，是非参考にしてください(^^)/
同期発電機の原理
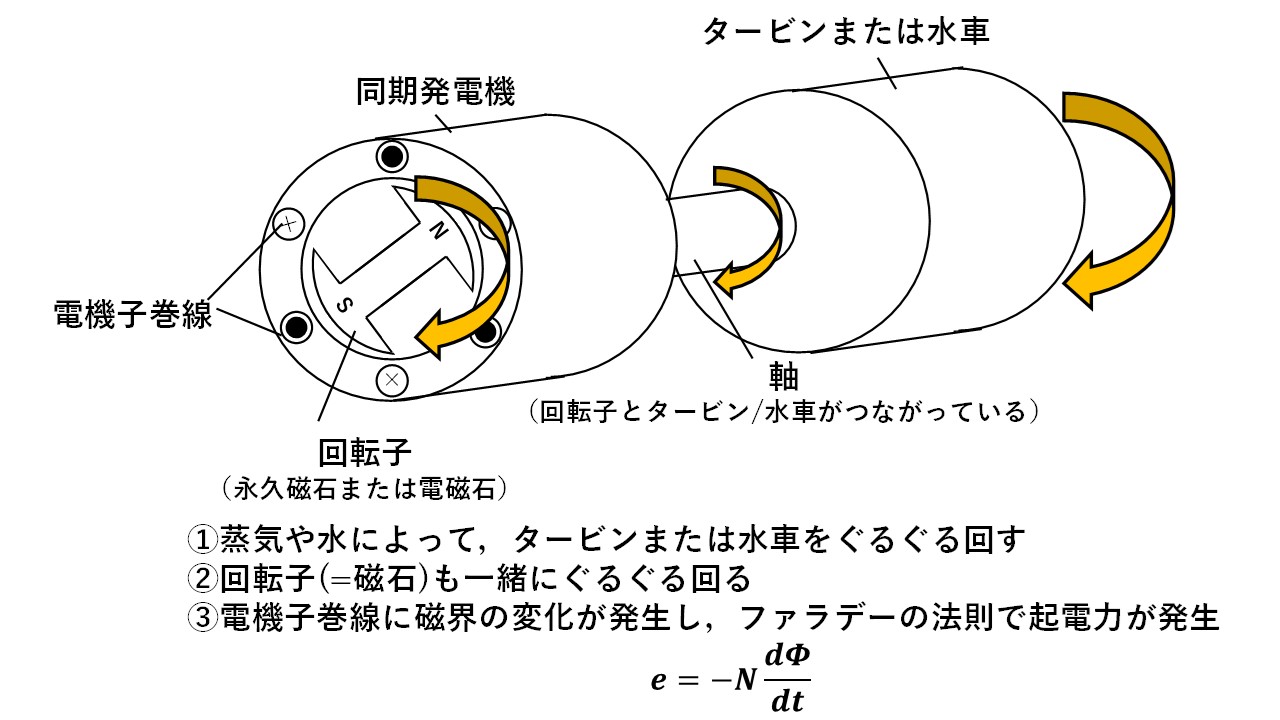
図1に同期発電機の原理を示します！磁石をぐるぐる回して電機子巻線に磁界の変化を発生させ，ファラデーの法則により電圧を発生させる，というのが，同期発電機の原理になります(^^)/ 磁石をぐるぐる回すために，磁石と軸でつながったタービンまたは水車をぐるぐる回します！（火力発電機または原子力発電機であれば蒸気でタービンを回します、水力発電機であれば水の力で水車を回します！）
図1 同期発電機の原理
同期発電機の誘導起電力の公式
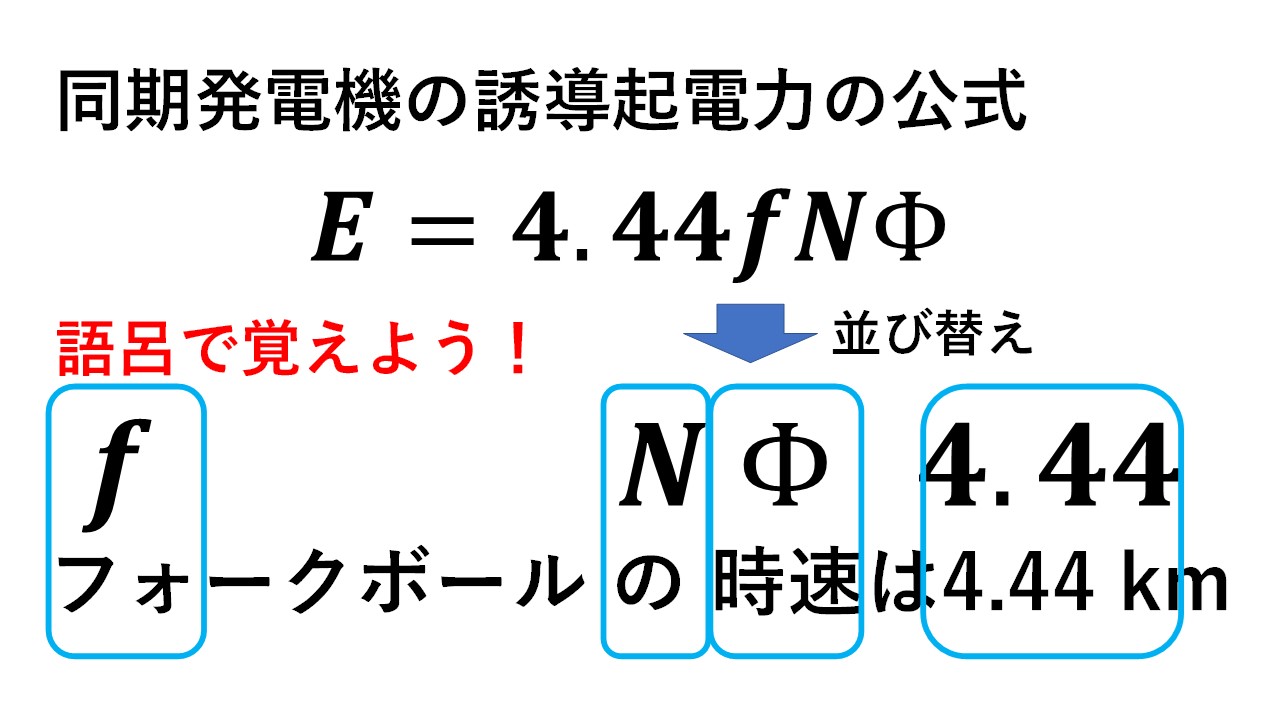
同期発電機の誘導起電力の公式を，図2に示します！ 4.44という数字が非常に唐突感がありますね（笑） 以降ではこの公式を導出しますので，その時にこの4.44という数字がどこからくるのかなども合わせて押さえておきましょう(^^)/
図2 同期発電機の誘導機起電力の公式
語呂で公式を覚えよう！
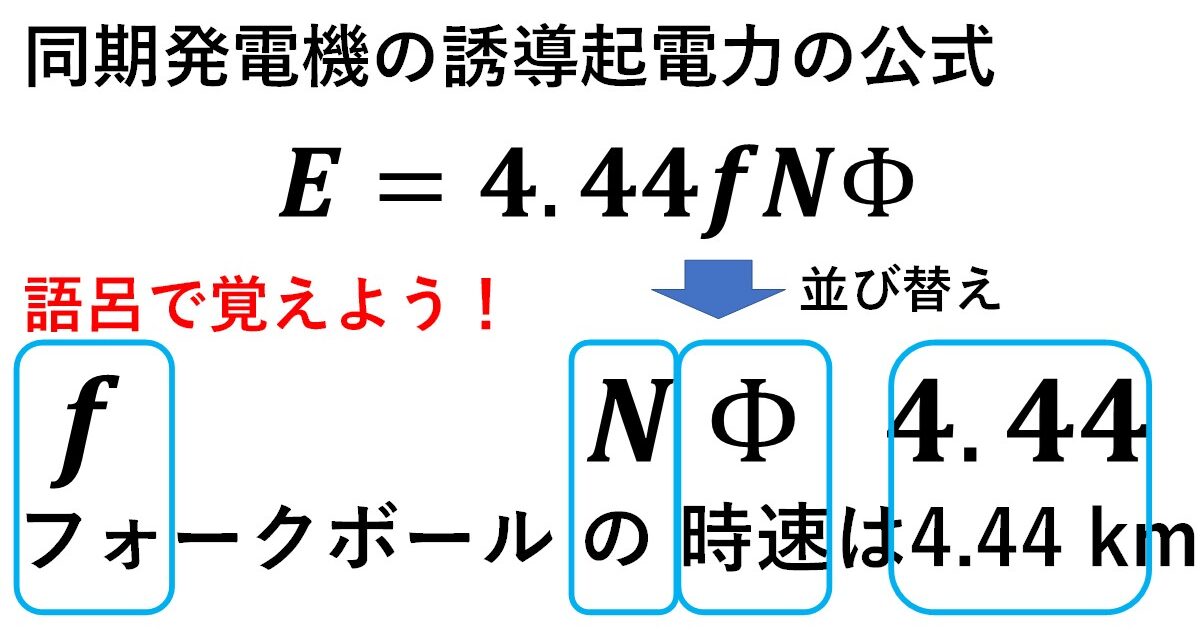
同期発電機の誘導起電力の公式の覚え方を，著者なりに考えてみました（笑） 図3に筆者が考案した語呂を示します！もしなかなか公式を覚えられない方で，この語呂が覚えやすかったら，ぜひ参考にしてみて貰えると嬉しいです(^^)/
図3 語呂で覚える同期発電機の誘導起電力の公式
-
（参考）同期機など回転機の基礎を0から勉強したい方にオススメの書籍
今回の記事では，同期機の原理を中心に解説していますが，実際に大学の講義の試験の問題や電験3種の試験を解くには，もっと幅広い知識が必要になります！以下の書籍は，同期機などの回転機（直流機，誘導機，同期機）を0から勉強する初学者の方にとってもオススメの本です！沢山のイラストを用いて，同期機を0から丁寧に説明しているだけでなく，変圧器や直流機、誘導機についても丁寧に解説されています！また，付録の問題集では，電験3種の過去問が単元毎に整理されているので，理解度を確認するのに非常に便利です！著者も愛用していますので，是非読んでみてください(^^)/
公式を導出してみよう！
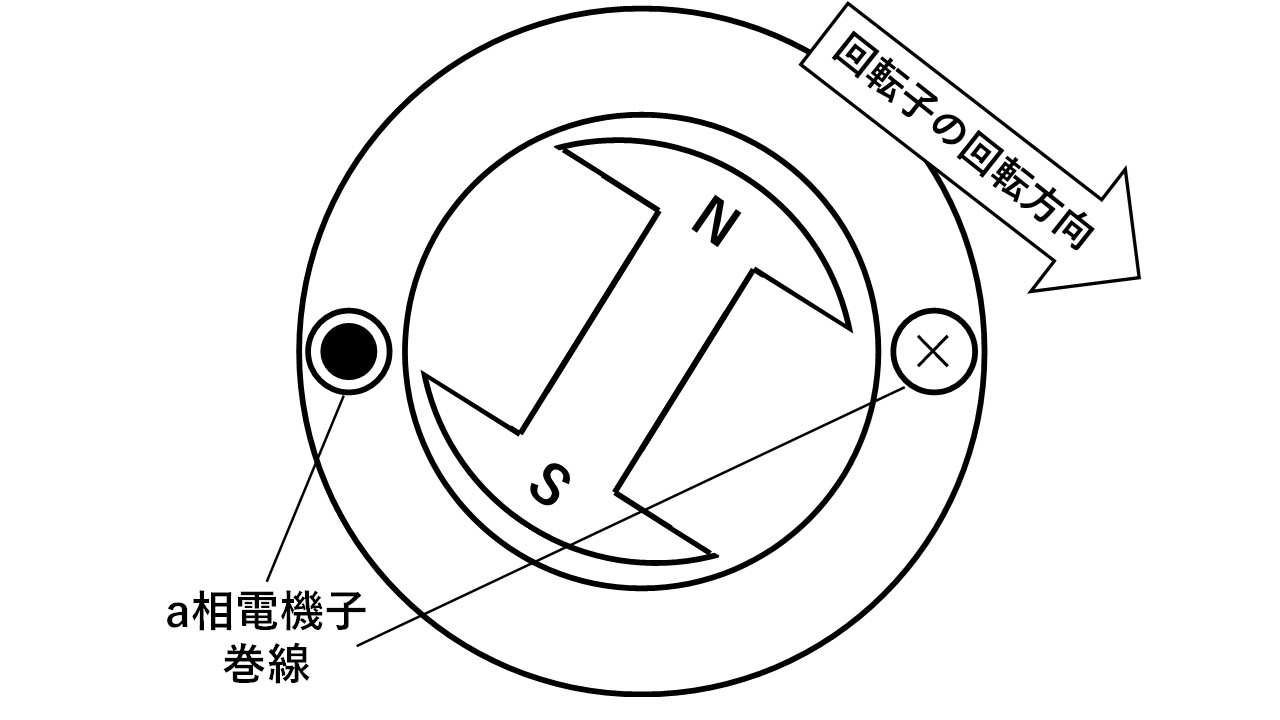
図4のように，2極機の同期発電機を例に同期発電機の誘導起電力の公式を導出します！a相の誘導起電力の求め方が分かれば，b相c相は位相が120[deg]ずつずれるだけですので，ここではa相の電機子巻線に生じる誘導起電力の公式を導出します！同期発電機の誘導起電力の公式の導出は，以下の4つのステップで導出できます(^^)/ 一つずつ見ていきましょう！
ステップ①：周方向に伸ばして，平べったくして考える
ステップ②：磁束密度Bの式を理解する
ステップ③：磁束密度Bから磁束Φを計算する（公式：Φ=BSを利用）
ステップ④：磁束Φから誘導起電力Eを計算する（ファラデーの法則：e=-NdΦ/dtを利用）
図4 誘導起電力の公式の導出対象
ステップ①：周方向に伸ばして、平べったくして考えてみよう！
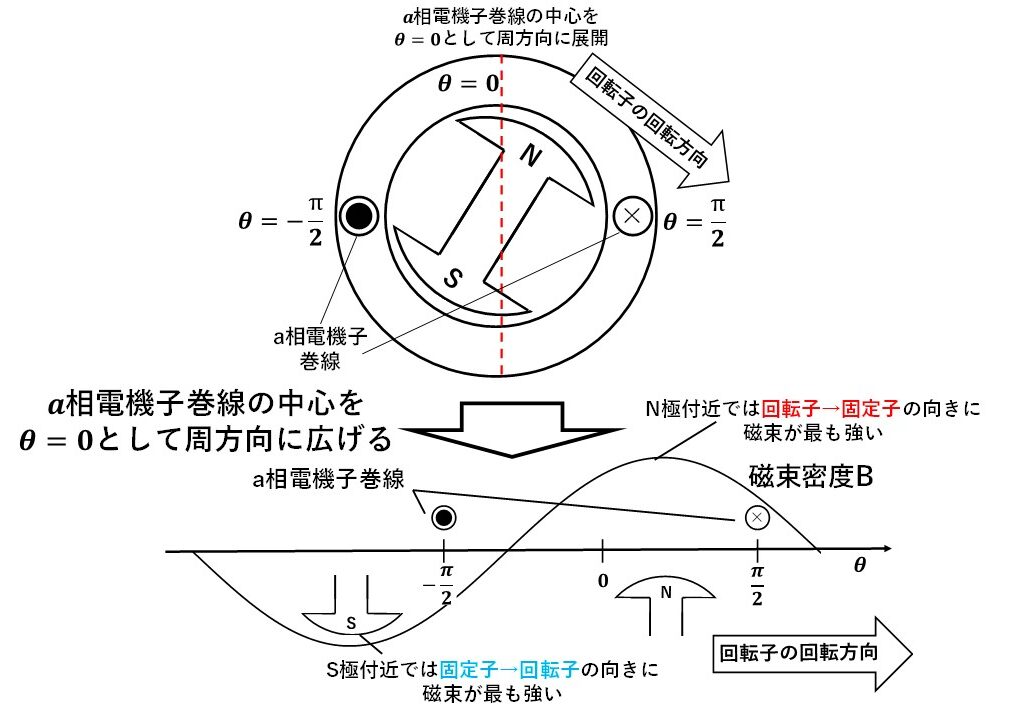
まず図5のように，発電機を周方向に伸ばして平べったく考えてみましょう！このとき，a相の電機子巻線の中心を0として考えてみましょう！すると，a相の電機子巻線の中心をθ=0と定義したので，実際の巻線はそれぞれ中心から90度離れた位置になり，図5の下図のようになります！ここで，磁束密度は，N極S極付近で最も強く，N極とS極では磁束の向きが反対なので（N極では回転子→固定子の向き、S極では反対），磁束密度は図のように正弦波状になります(^^)/
図5 周方向に伸ばして，平べったくして考えてみよう！
少し時間を進めてイメージをつかもう！
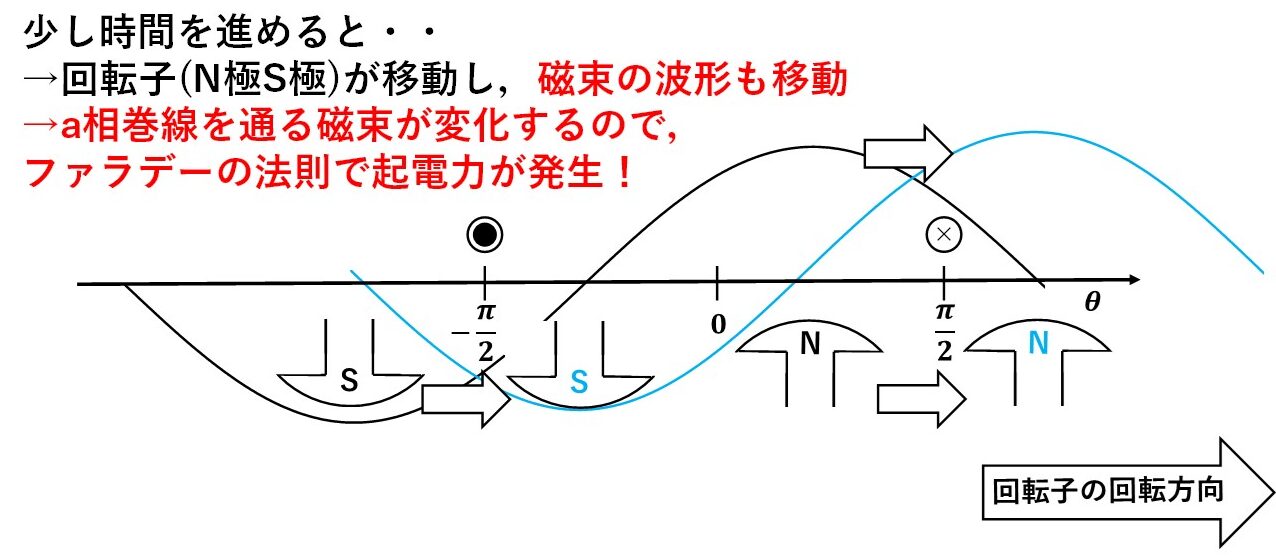
イメージをつかむために，少しだけ時間を進めてみましょう！すると，a相の電機子巻線は固定されているので動かないのに対して，回転子はぐるぐる回っているのでN極とS極の位置が移動します！またN極やS極の位置が最も磁束が強いので，当然ですがNS極の移動に伴って磁束密度の波形も移動します！ すると，a相の電機子巻線を通る磁束が変化しますので，ファラデーの法則で起電力が発生しそうですね(^^)/
図6 少し時間を進めて，イメージをつかもう！
ステップ②：磁束密度Bの式を理解しよう！
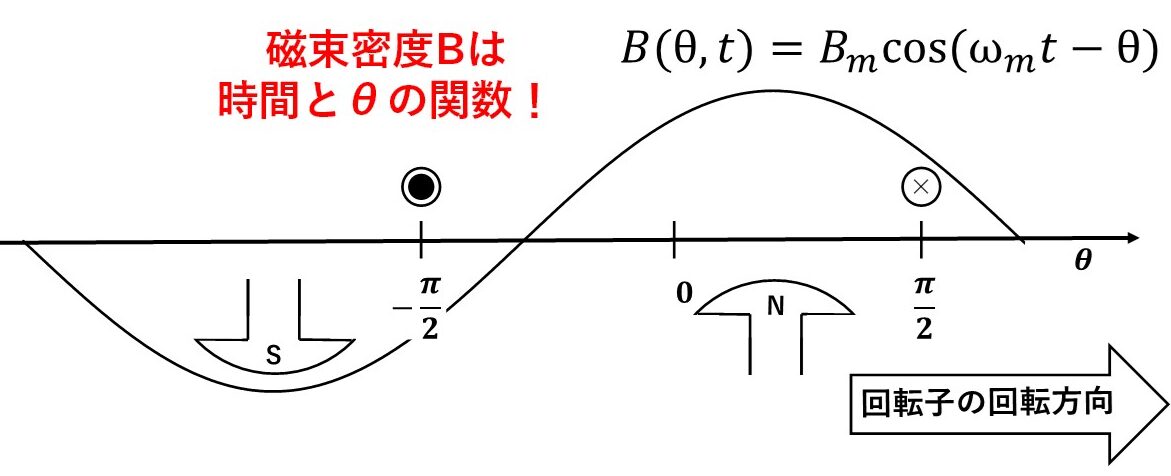
同期発電機の電圧が発生する原理がなんとなく分かったところで，実際に式を使って理解していきましょう！図5や図6で出てきた磁束密度Bを式で表すと，図7のように時間だけでなくθ（つまり場所）の関数になります！普段，時間tの関数を扱うことは多いですが，変数が2つの関数はあまり扱わないので，初学者にとってはなかなか理解が難しいと思います！そこで，以降ではまずこの磁束密度Bの式について少し補足説明をします(^^)/
図7 磁束密度は時間tと場所θの関数
磁束密度B(θ,t）の式の意味を理解しよう！
磁束密度の式は時間tと場所θの2つによって変化するので，一見すると複雑に見えますが，磁束密度の時間変化が知りたい場所のθの値を，磁束密度の式B(θ，t）に代入すれば，それがその場所での磁束密度の時間波形になります！これにより，θが固定されて時間tのみの関数となり，普段扱いなれた関数になります！
例1) θ=0の場所の磁束密度が知りたい場合
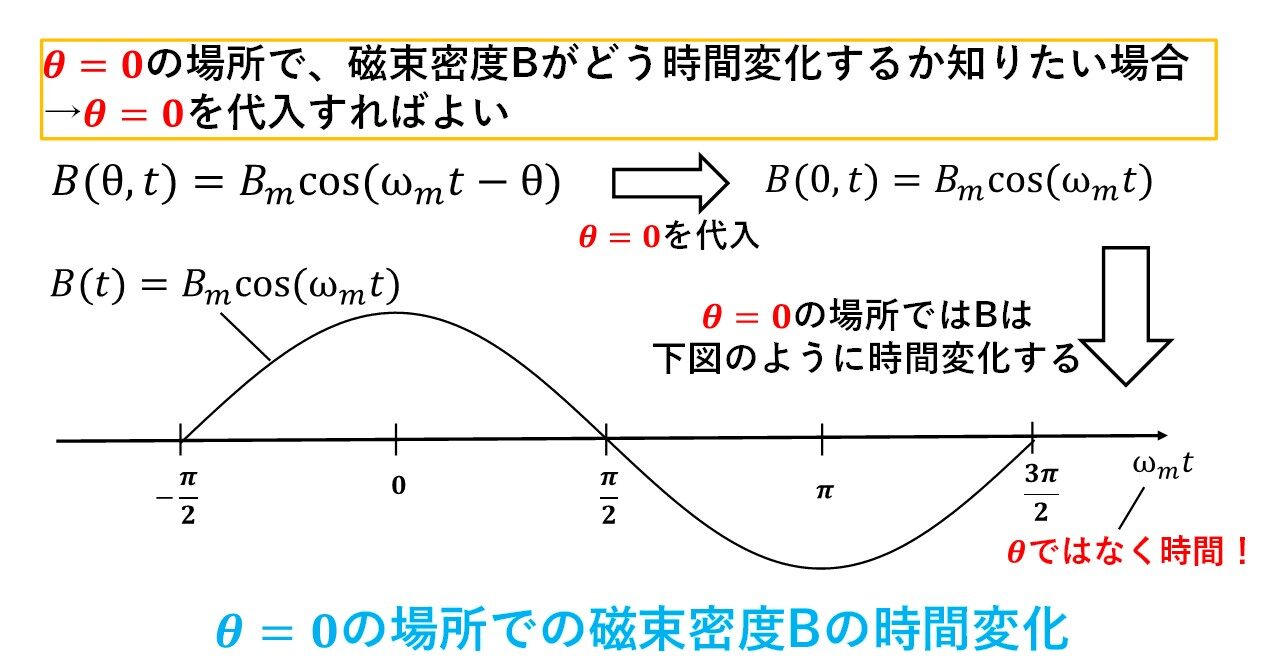
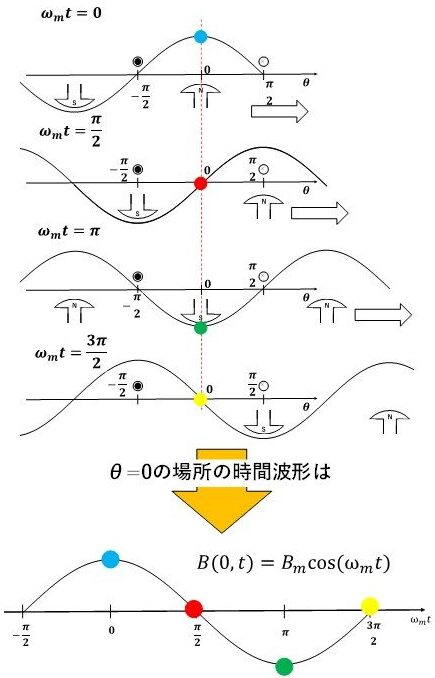
例えば，θ=0の位置の磁束密度の時間変化が知りたい場合は，磁束密度の式B(θ，t）にθ=0を代入しましょう！すると，磁束密度の時間波形は図8のようにBmcos(ωmt)となり，これがθ=0の場所の磁束密度の時間変化になります(^^)/ 本当かどうか実際に図9を見て確認してみましょう！N極S極は時間とともに少しずつ回転する（この図では右側に進む）ので，磁束密度の波形も時間とともに少しずつ右に移動します！θ=0の位置ではωt=0，π/2，π，3π/2の順に最大→0→最小→0となっており，図9一番下の時間波形Bmcos(ωmt)の通りになっているのが分かりますね！
図8 θ=0の場所での磁束密度の時間変化が知りたい場合
図9 θ=0の場所の時間波形がBmcos(ωmt)になっているかの確認
例2) θ=π/2の場所の磁束密度が知りたい場合
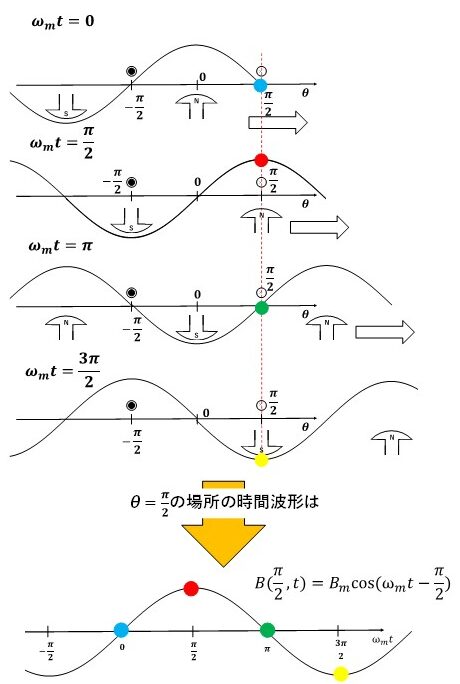
θ=π/2の位置の磁束密度の時間変化が知りたい場合も同様で，磁束密度の式B(θ，t）にθ=π/2を代入しましょう！すると，磁束密度の時間波形は図10のようにBmcos(ωmt-π/2)のようになります！そして，図11を見ると，Bmcos(ωmt-π/2)がθ=π/2の場所の磁束密度の時間変化にちゃんとなっていることが分かりますね(^^)/
以上から，B(θ，t）=Bmcos(ωmt-θ)という式は，ある場所θでの磁束密度の時間波形を表す式になっているだけで，見た目ほど難しくないことが分かったかと思います(^^)/
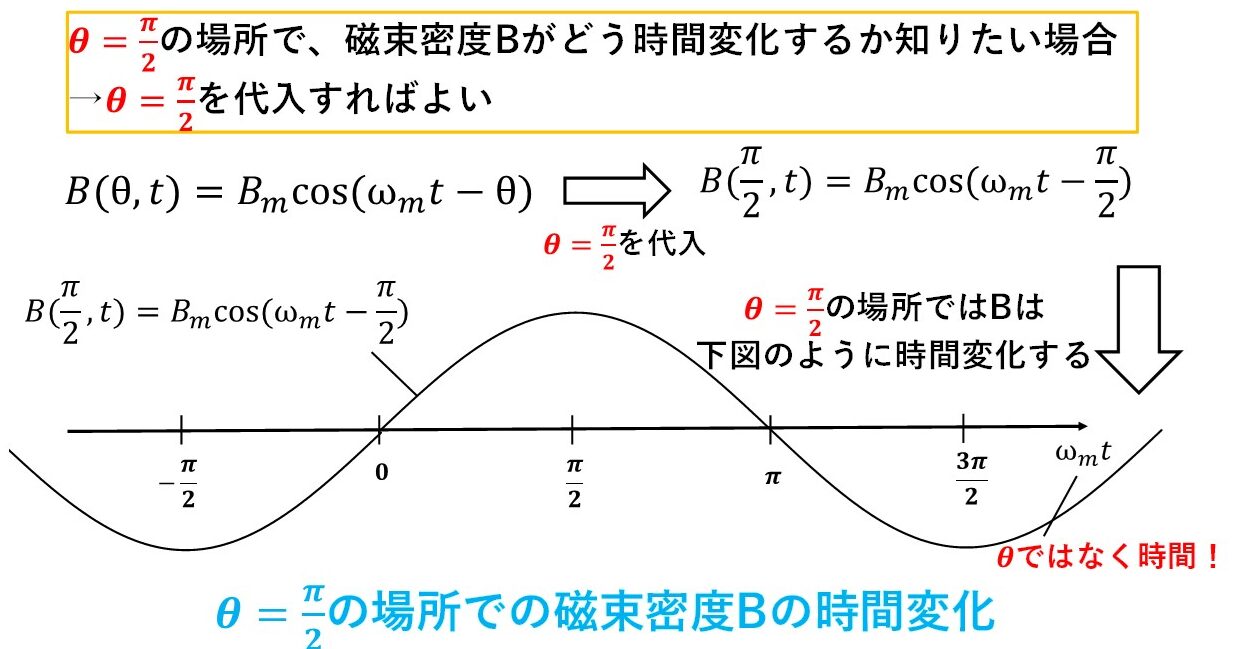図10 θ=π/2の場所での磁束密度の時間変化が知りたい場合
図11 θ=π/2の場所の時間波形がBmcos(ωmt-π/2)になっているかの確認
ステップ③：磁束Φを計算しよう！
磁束Φ＝磁束密度B×面積Sで求まる！
磁束密度Bの式が分かったところで，続いて磁束Φを計算しましょう！ 磁束密度とは，「密度」という言葉通り，磁束を面積で割った値です！なので，逆に言えば，磁束密度Bに面積Sをかければ，その面積を通る磁束Φを計算することができます！
a相の電機子巻線を通る磁束を計算してみよう！
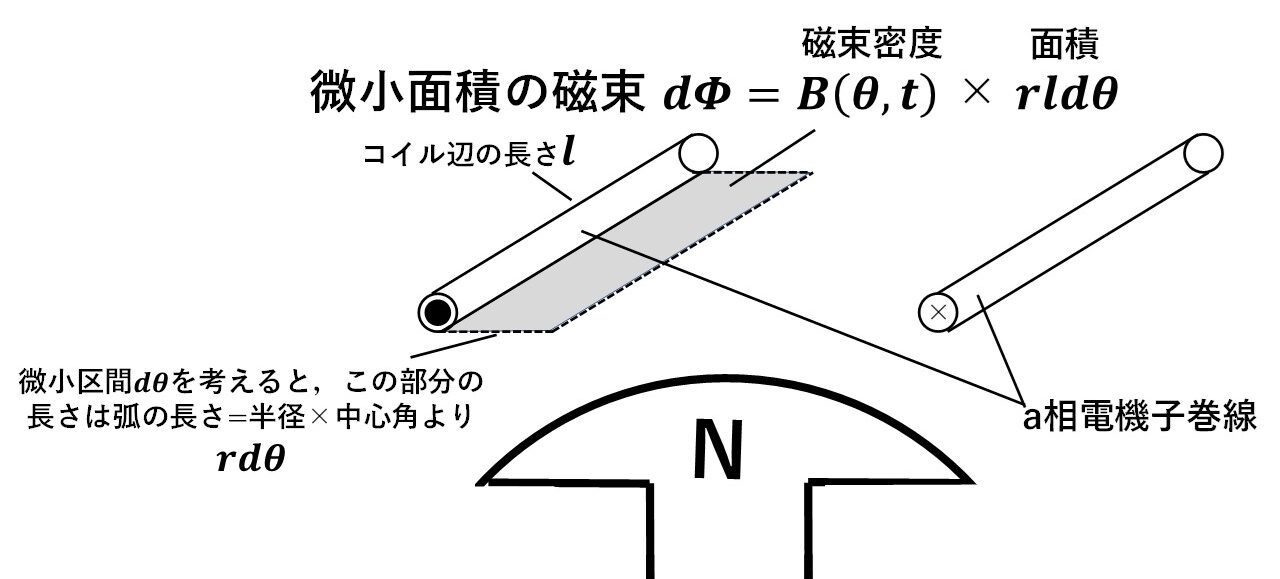
a相の電機子巻線を通る磁束を実際に計算してみましょう！電機子巻線のコイル辺の長さをl，回転子の半径をrとすれば，微小区間の面積dΦは，図12のように求まります！
図12 微小区間の面積を考えよう！
最終的に知りたいのは，a相の電機子巻線全体を通る磁束なので，図13ように積分計算をして，a相の電機子巻線を通る磁束Φが求まります！
（補足）Φ=BSなんだから，磁束密度Bの式にa相電機子巻線の面積（=l×r×π)をかけて終わりじゃないの？何で積分なんかしなくちゃいけないの？と思った方がいらっしゃるかもしれませんが，単純な掛け算で済むのは，磁束密度Bがどの場所でも同じ大きさ（=θによらず一定）の場合だけです！実際には，場所θによって磁束密度の大きさが変わるため，積分が必要になります(^^)/
図13 全体の面積を考えよう！
後は，得られた磁束の式に，磁束密度Bの式を代入して計算していくと，以下の通り最終的にはΦ=2Bmrl*cos(ωmt)という式が得られます！ ここで，2Bmrlはcosωmtの係数であるということからも分かる通り，磁束Φの最大値になりますので，これをΦmと定義すれば，磁束ΦはΦ=Φm*cos(ωmt)という式になります(^^)/
図14 a相電機子巻線を通る磁束Φの導出
ステップ④：誘導起電力Eを計算しよう！
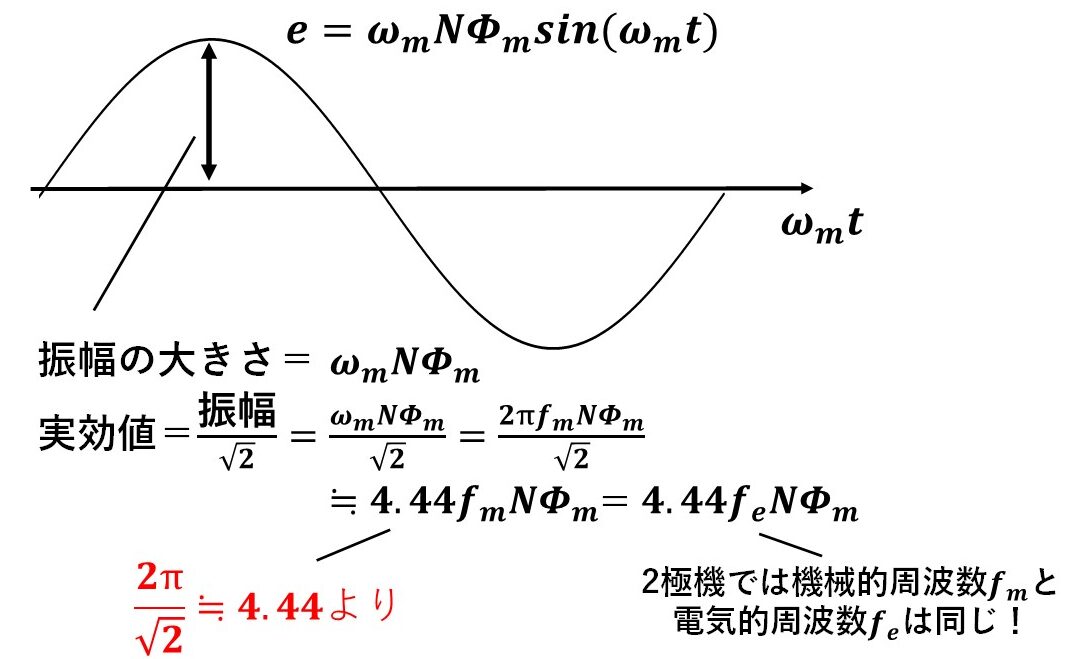
さて，a相の電機子巻線を通る磁束Φが求まったので，最後にファラデーの法則により誘導起電力Eを計算しましょう！a相の電機子巻線の巻数をNとすれば，電機子巻線に生じる誘導起電力は以下の通り計算できます(^^)/
ここで，ωmNΦmはあくまで誘導起電力の振幅(つまり最大値）なので，実効値ではありません！交流では実効値がよく使われますので，√2で割ってあげましょう！また，ωm=2πfmであることに注意すると，最終的にE=4.44fNΦの式が導出できます！ 4.44という唐突な数字は，2π/√2を計算したものだったんですね(^^)/
図15 a相電機子巻線に生じる誘導起電力
以上が同期発電機の誘導起電力の公式でした！今回は簡単のために2極機の例を扱ってきましたが，多極機の場合は，もう少し公式の導出が複雑になりますが，最終的に導出される誘導起電力の公式は図2と全く同じです(^^)/ こちらはまた別の機会に公式の導出方法を紹介できればと思います！
今回の記事はここまでです！この記事が皆さんの役に少しでもなっていれば嬉しいです(^^)/
