こんにちは,ハヤシライスBLOGです!今回は変圧器の等価回路についてできるだけ分かりやすく解説します。
変圧器を通る2種類の磁束について
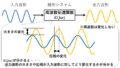
図1の通り,変圧器のそれぞれの巻線を通る磁束は,以下の2種類に分けられます!(^^)/
・主磁束⇒2つの巻線を通る磁束。メインの磁束
・漏れ磁束⇒それぞれの巻線のみを通る磁束
要するに,電圧を1次側と2次側で変えるという変圧器のメインの役割を担うのは主磁束ですが,それぞれの巻線を流れる電流が作る磁束はすべて主磁束になるわけではなく,一部は自分自身の巻線しか通らない漏れ磁束になります(^^)/
電気回路上では磁束ではなく電圧で扱いますが,実は主磁束と漏れ磁束とで電気回路上の表現は違います!1つずつ見ていきましょう(^^)/
図1 変圧器を通る2つの磁束について
主磁束の等価回路について
図2の左図は,主磁束のみを取り出した図になります。この図の通り,主磁束は2つの巻線を通る磁束になります!そのため,ファラデーの電磁誘導の法則における磁束の微分(磁束の変化)は,2つの巻線で同じになります!したがって,主磁束により発生する電圧の大きさは巻数比によって決まり,図2の右図のように理想変圧器で表すことができます(^^)/
ファラデーの電磁誘導の法則や変圧器の原理については,以下の記事を参考にしてください(^^)/
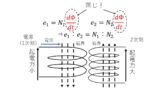
なお理想変圧器では,電流がアンペアターンの法則により巻数の逆比になることも重要な点ですので,しっかりと覚えておきましょう!
図2 主磁束の等価回路
漏れ磁束の等価回路について
図3の左図は,それぞれの巻線の漏れ磁束のみを取り出した図になります。漏れ磁束はそれぞれの巻線しか通りませんので,1次側と2次側の漏れ磁束によって発生する電圧は巻数比にはなりません!
漏れ磁束により発生する電圧を,先程と同様にファラデーの電磁誘導の法則で考えると,Φ=Nφ=Liと,d/dt=jωに注意すれば,図3左上の式の通り,漏れリアクタンスの形で表すことができます(^^)/
図3 漏れ磁束の等価回路
変圧器の等価回路(励磁回路なし)
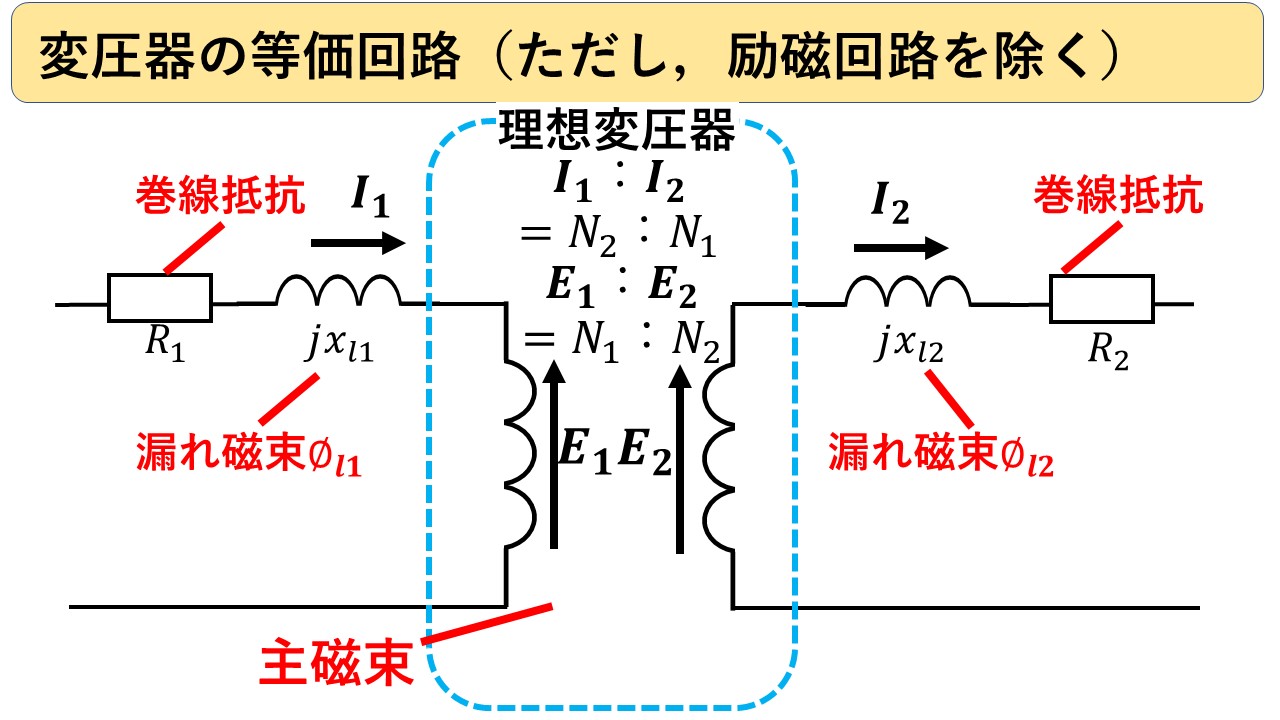
これまでの説明で,主磁束は理想変圧器で,漏れ磁束は漏れリアクタンスで電気回路上で模擬することができると分かりました! 変圧器には抵抗がありますからそれを考慮すると,変圧器の等価回路は図4になります!
図4 変圧器の等価回路(励磁回路を除く)
変圧器の励磁回路について
さて,これで変圧器の等価回路の説明を終わりたいところですが,実は図4の等価回路では完全に変圧器を表現できていません。実は励磁回路というものが欠けています! まずは,そのことを確認していきましょう!
励磁回路を無視した場合の矛盾
励磁回路を無視した図4の等価回路の場合,完全に変圧器を表現できていないため,おかしなことが起こります!以下ではそれを見てみましょう(^^)/
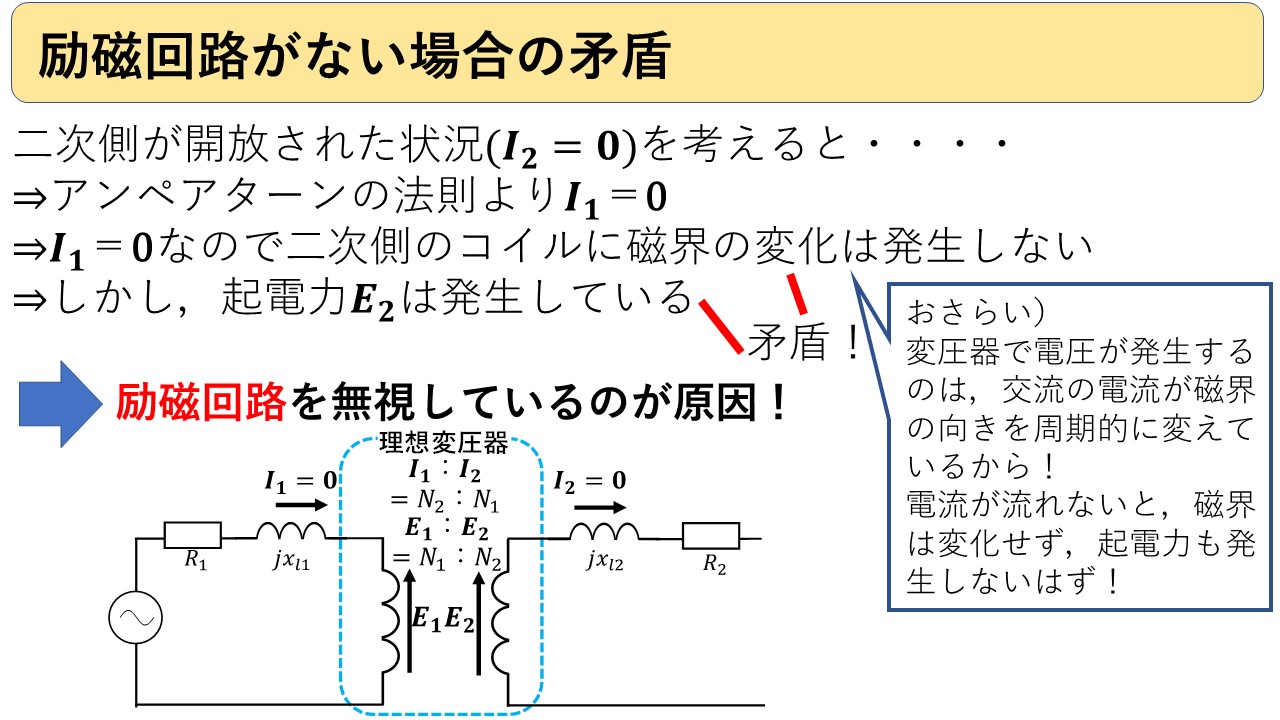
簡単のために,図5のように1次側は電源につながっていて,2次側には何もつながっていない状態(=2次側が開放された状態)を考えます。通常の変圧器との違いは,単に2次側が開放されている点だけです。
図5 励磁回路を無視することにより生じる矛盾
2次側は開放されているので,2次側の電流は当然0になります。一方で1次側の電流は,アンペアターンの法則でこちらも0になります。つまり,1次側も2次側も電流が流れていない状態になります。
ここで,おかしな状態が生じます。おさらいですが,変圧器に電圧が発生するのは,交流電流が作る磁界の向きが周期的に変化し,その磁束の変化を打ち消すためにファラデーの法則により起電力が発生するからでした。しかし,図5を見ると,1次側と2次側に起電力E1,E2が発生していますが,1次側も2次側も電流が流れないので,磁束の変化はおろか,そもそも磁束が発生しません!磁束がそもそも発生していないはずなのに,何故か電圧が発生するという不思議な状態が起こっています! これは,励磁回路を忘れていることが原因です(^^)
励磁回路とは
励磁回路とは,励磁電流の効果を電気回路上で表現した回路になります(^^)/
励磁電流とは,以下の2つの成分に分けられます! 先ほどの例では,以下の磁化電流を考慮していなかったため,おかしなことが起きてしまっていました(^^)/
・磁化電流⇒主磁束を作る電流成分
・鉄損電流⇒鉄損分を供給する電流成分
なお,鉄損とは大きくヒステリシス損と渦電流損に大別されます!
・ヒステリシス損:鉄心中の分子相互間の摩擦によって生じる損失
変圧器鉄心の磁束が変化することで,鉄心中の磁気分子の向きや配列が変化し,分子相互間の摩擦損が発生する。
・渦電流損:鉄心表面に流れる電流によって発生するジュール熱
磁界が変化することで,鉄心に起電力が発生し,これによって生じる電流(渦電流)によってジュール熱が発生する。
変圧器の等価回路(励磁回路あり)
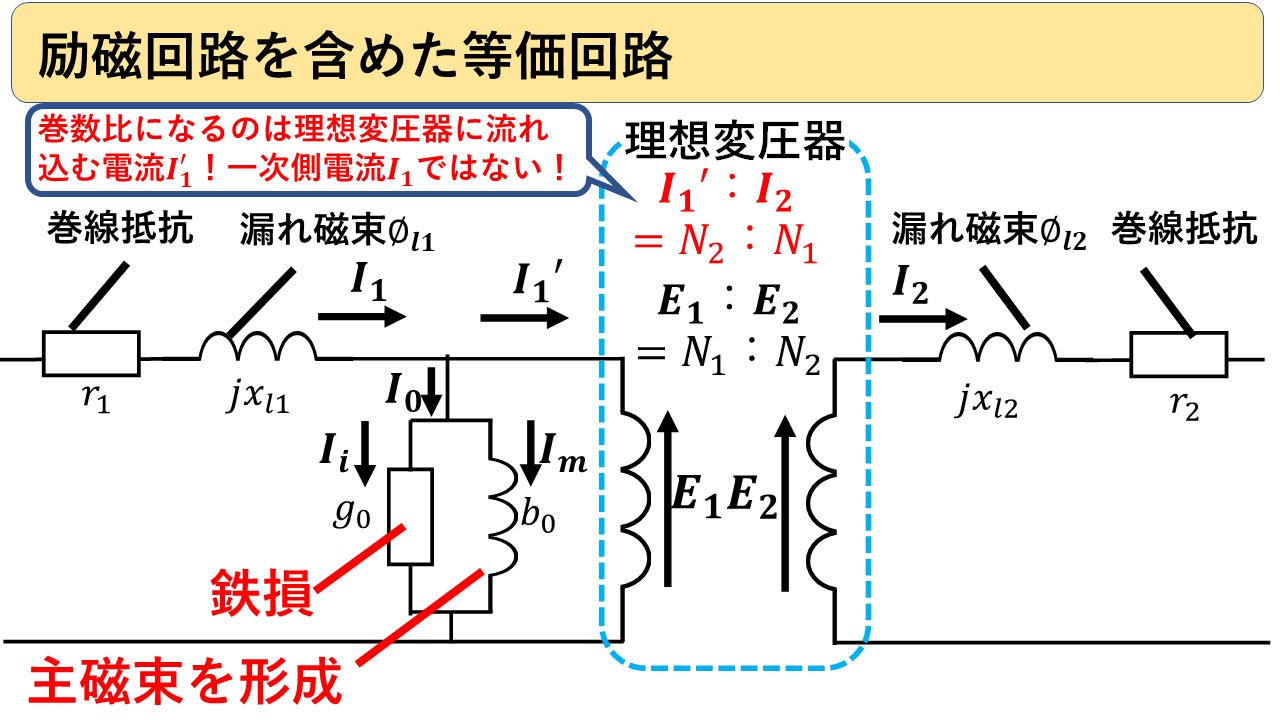
励磁回路を含めた変圧器の等価回路は,図6になります!図4と比べて,磁化電流Imと鉄損電流Iiが追加されており,主磁束を作る電流や鉄損が考慮されているのが分かります(^^)/
なお,g0を励磁コンダクタンス,b0を励磁サセプタンスと呼びます!
ここで,超重要ポイントです!アンペアターンの法則で電流が巻数の逆比になるのは,理想変圧器に流れ込む1次側の電流(=1次側電流から励磁電流を引いた残り)と2次側電流であって,1次側電流と2次側電流ではありません!! ここは,誤解のないようにおさえておきましょう(^^)/
図6 変圧器の等価回路(励磁回路あり)
変圧器等価回路の一次側換算
変圧器では,図6のように1次側と2次側を別々の回路として扱うのではなく,図7のように1つの回路に換算する場合があります! 最後に,2次側を1次側に換算した場合の等価回路を図7に示します(^^)/
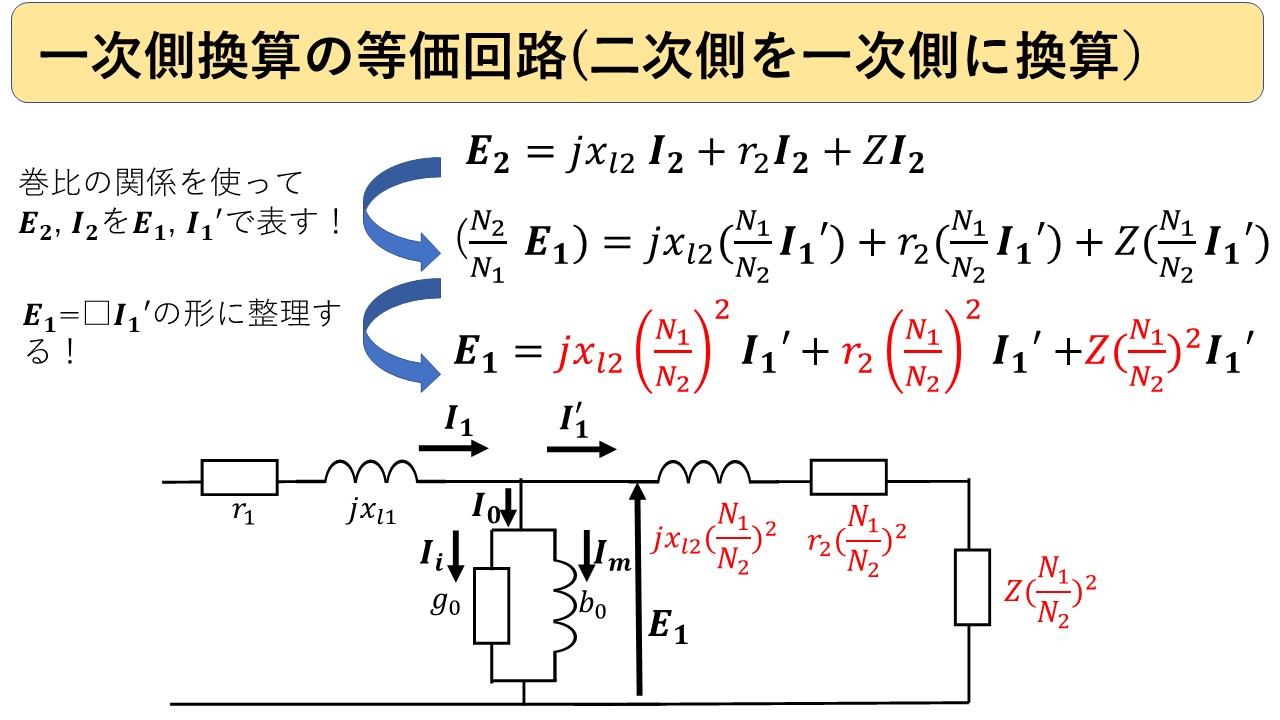
図7 変圧器等価回路(励磁回路あり)の1次側換算
まず2次側の回路方程式を立てます!
その後,巻数比の関係を使って,2次側電圧・電流を1次側電圧・電流の形で表します!(ただし,1次側電流は,励磁電流を除いた成分) 最後に,式を整理すると,2次側回路を1次側へ換算した場合の抵抗・リアクタンスが求まります(^^)/
例えば,1次側の方が2次側より電圧が大きい場合(=N1>N2の場合),2次側を1次側から見ると,本当の2次側の回路定数よりも大きく見えることになります(^^)/
以上,変圧器の等価回路についてでした!お疲れ様でした(^^)/