こんにちは，ハヤシライスBLOGです！今回は複素フーリエ級数展開の式から，フーリエ変換の公式を導出します！
フーリエ変換について
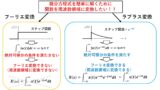
詳しくは，以下の「フーリエ変換を分かりやすく解説」の記事で説明していますが，フーリエ変換の考え方をざっくり説明すると，周期的な波形に対してしか使えないフーリエ級数展開を，非周期的な波形に対して使える形に変形したものです！具体的には，「非周期的な波形＝周期が∞の波形」とみなして，フーリエ級数展開を適用したものになります！したがって，フーリエ変換の公式は，フーリエ級数展開の式において周期T→∞とすることで導出することができます(^^)/
この記事では，フーリエ級数展開を複素数の形で表した複素フーリエ級数展開の式から出発して，フーリエ変換の公式を導出します！ある程度の前提知識があるとして話を進めますので，フーリエ級数展開やフーリエ変換の勉強がまだの方は，是非以下の記事を読んでみてください(^^)/
＜フーリエ級数展開について＞
＜フーリエ変換について＞
フーリエ変換とフーリエ級数展開の違い（数式編）
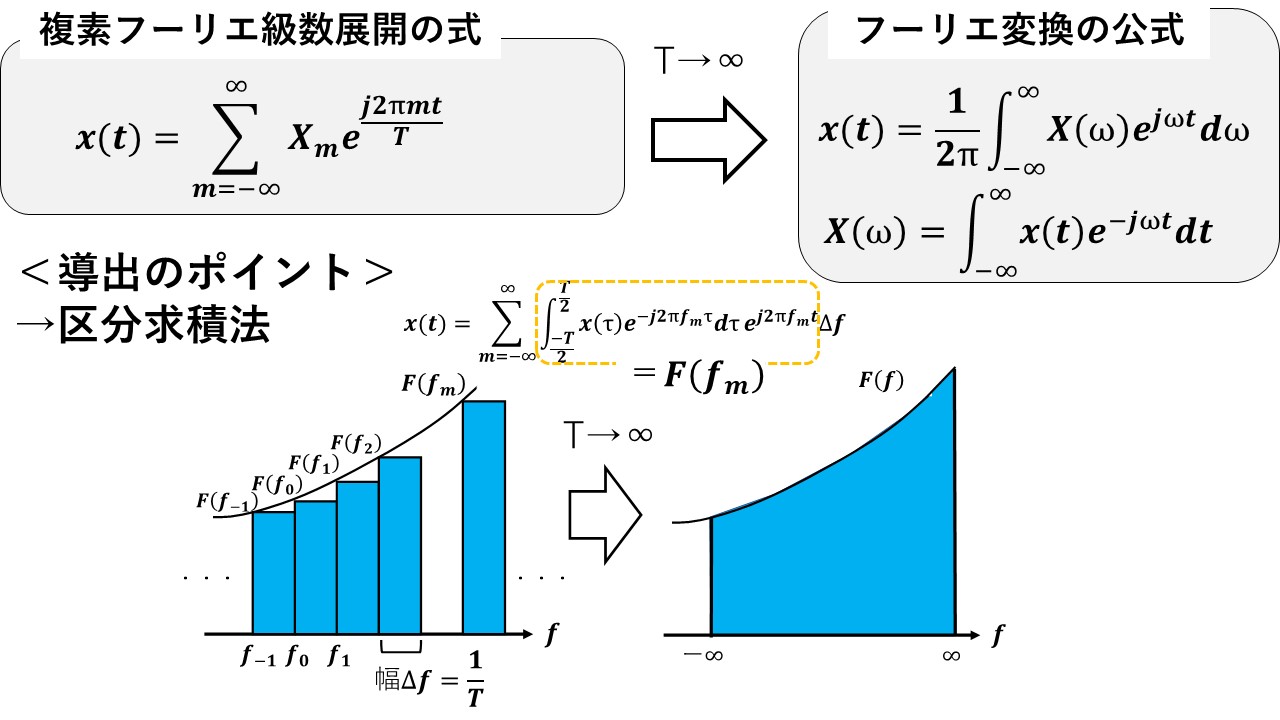
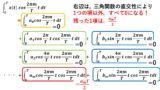
フーリエ変換と複素フーリエ級数展開の数式の違いをおさらいすると，図1になります。この記事では，左の複素フーリエ級数展開の式から右のフーリエ変換の公式を導出します(^^)/
図1 フーリエ変換と複素フーリエ級数展開の式の違い
フーリエ変換の公式導出
さっそく，複素フーリエ級数展開の式から出発して，フーリエ変換の公式を導出します(^^)/ 重要な点なので繰り返しになりますが，フーリエ変換はフーリエ級数展開に対して周期Tを∞とすることで，非周期的な波形に対してもフーリエ級数展開を適用できる形にしたものです！これは以下の導出過程で使いますので，覚えておきましょう(^^)/
複素フーリエ級数展開の式に複素フーリエ係数Xmの式を代入し，fmやΔfを以下のように定義すると，複素フーリエ級数展開の式は以下のように変形できます！
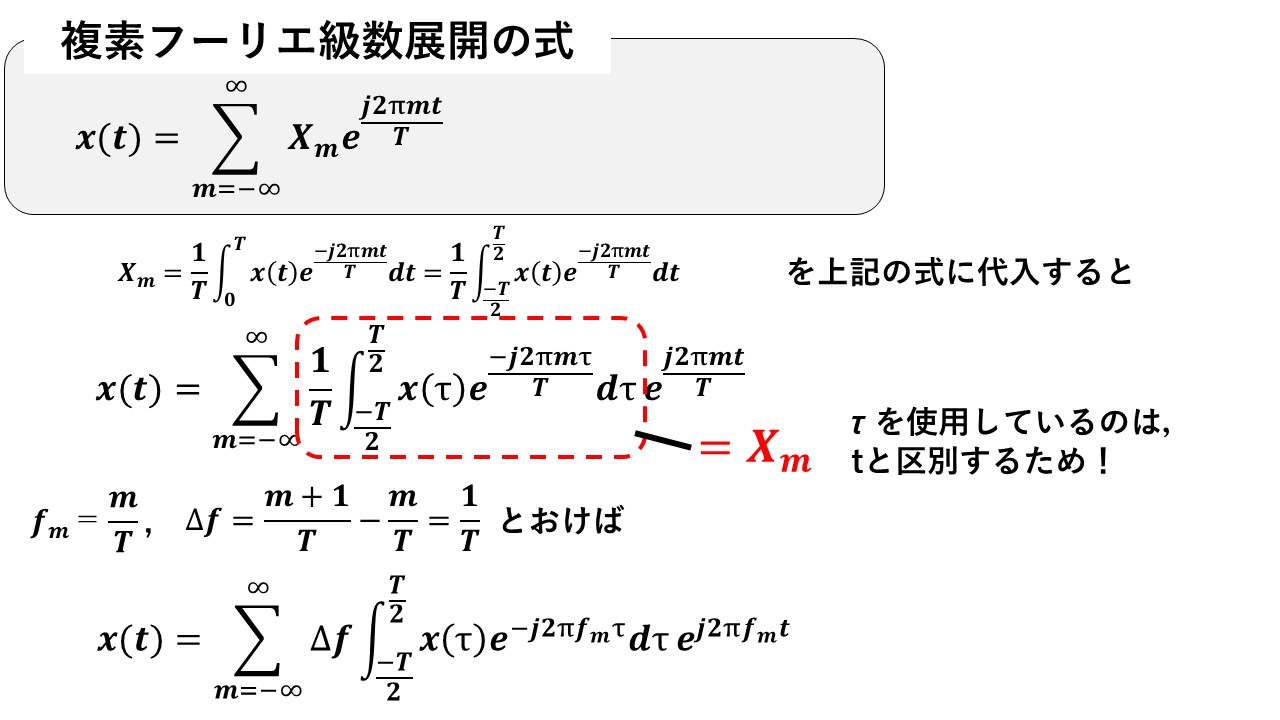
ここで，以下の数式の赤枠で囲んだ項をF(fm)と定義すると，x(t)は右下の図のように，横の幅がΔf，縦の幅がF(fm)の長方形をたくさん足し合わせていった面積の総和に等しいという式が得られます！
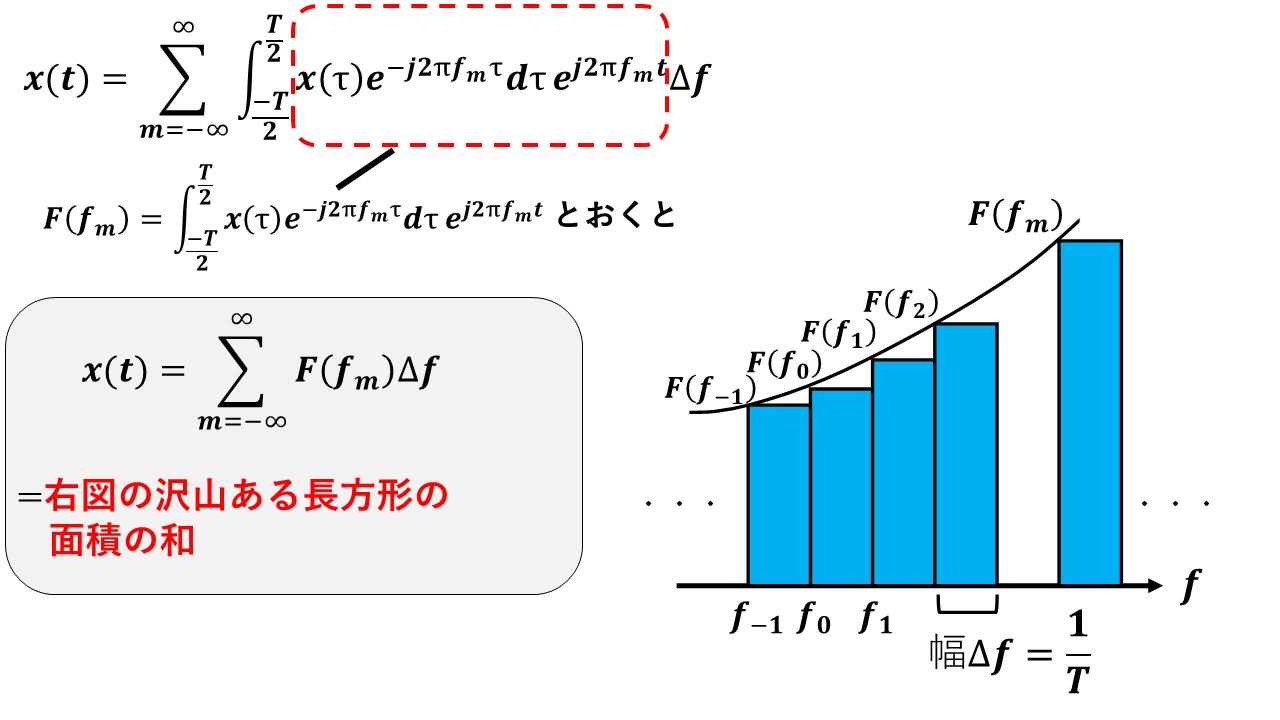
ここで，ようやくT→∞を考えます！
T→∞とすると，Δf=1÷T→1÷999999999.9・・・→0になるので，限りなく長方形の幅が0に近くなります！すると，左図の長方形の面積の総和は，右図のようにF(f)の関数をf=ー∞～∞まで積分した値に限りなく近くなります！まさに，高校数学で習った区分求積法の発想ですね(^^)/（※1）
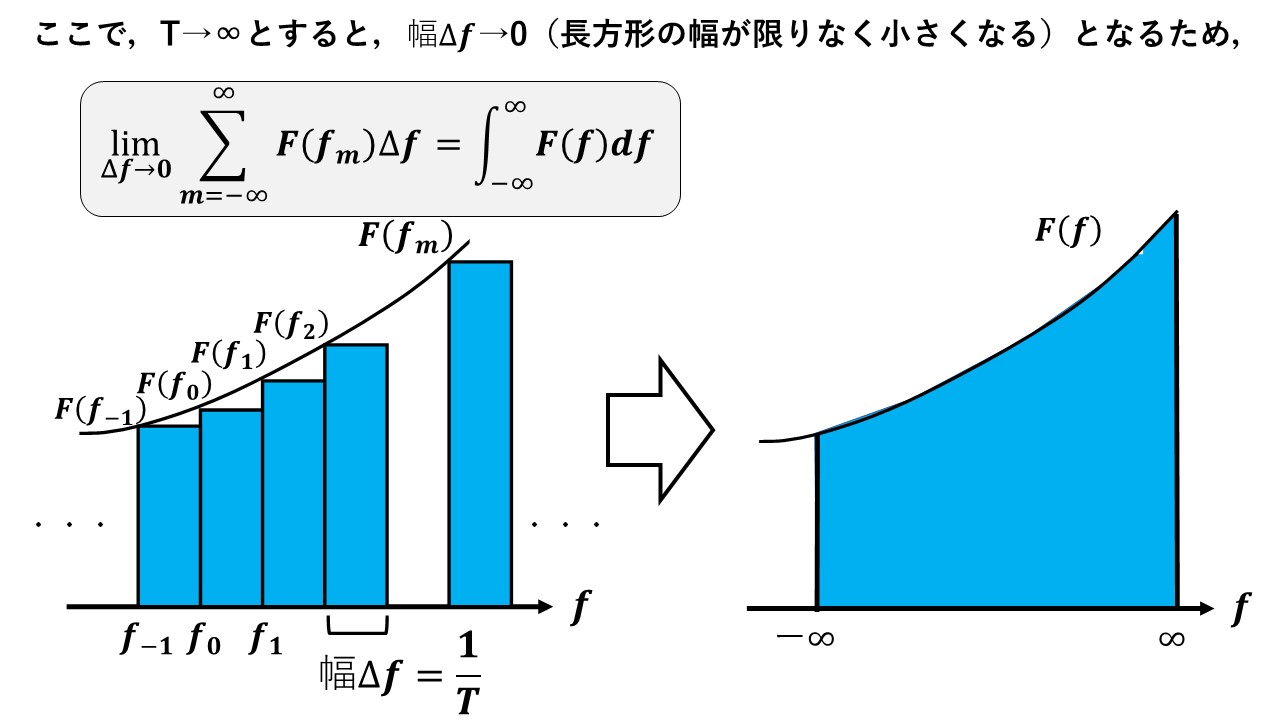
結果として，T→∞を考えると，Σ→∫，fm（離散的）→f（連続的），Δf（離散的）→df（連続的）になるので，これらを考慮すると，F(f)はF(fm)から以下のように導かれ，x(t)はその下の式で表されます(^^)/
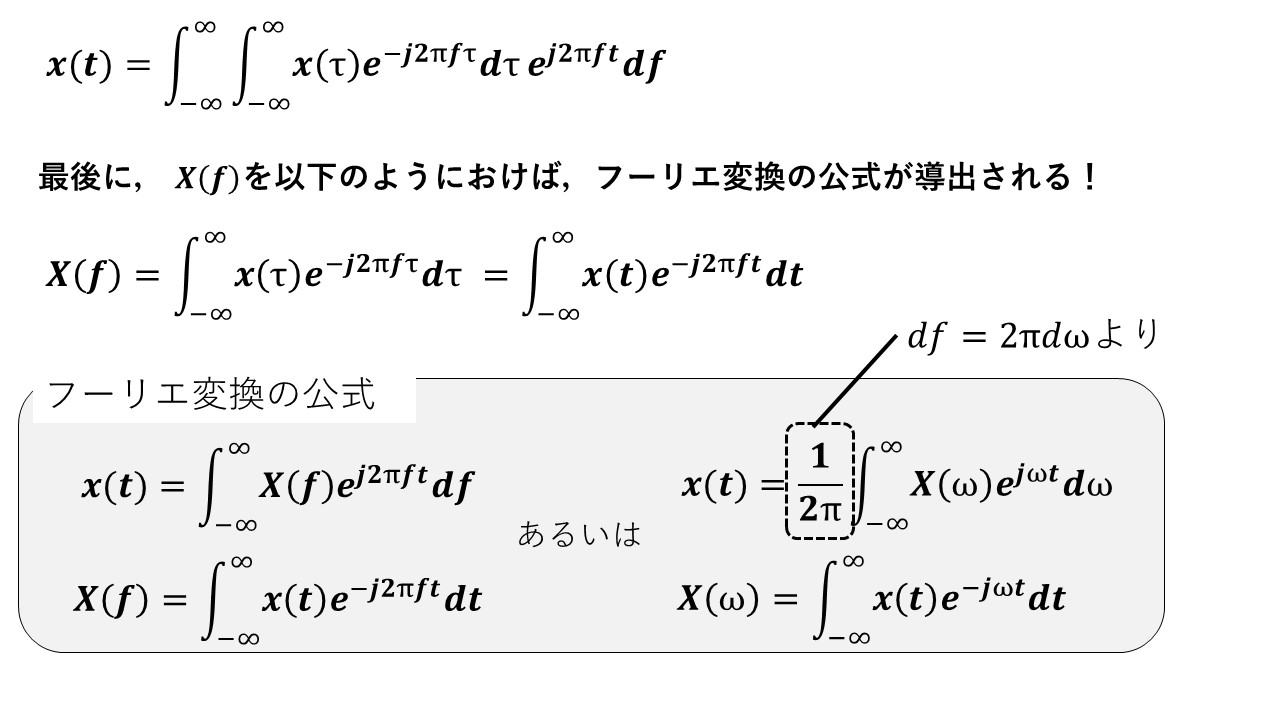
最後に，X(f)を定義すれば，フーリエ変換の公式が導出されます(^^)/
なお，ここまではｆで式変形を考えてきましたが，ωの場合のフーリエ変換の公式は，ω=2πf，dω=2πdfとすれば導くことができます！
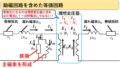
ちなみに以下の図では，ωで考えた場合のx(t)の式に，1/(2π)の係数が付いていますが，教科書によってはこれを1/√(2π)とし，さらにX(ω)の係数にも1/√(2π)をつける場合があります。要は，1/(2π)を2つに分けて書いているわけですね。
どちらで覚えても結果は変わりませんが，定義的には以下の図（=x(t)の式に1/(2π)の係数をつけ，X(ω)には係数なし）になるので，頭の片隅に入れておきましょう(^^)/
(※1)関数のフーリエ変換を求めるための条件（→ラプラス変換の導入）
最後に，記事の中で出てきた※1について補足します
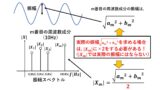
上記の区分求積法について説明した際，何も断らず-∞～∞までの積分を考えましたが，実はこの積分を考えるためには，条件が付きます！
上記が，関数のフーリエ変換を求めるための条件となります！①の条件は，多くの関数が満たすので問題ないとしても，②の条件は意外と多くの関数が満たせません（例えば，代表的な関数であるステップ関数なども満たせません）。これがフーリエ変換の弱点でもあります！つまり，フーリエ変換は非常に便利な考え方ですが，上記の条件を満たす関数に対してしか使えないのです！
実はこの点を克服したのが，ラプラス変換です！ラプラス変換については，別の記事でまとめます(^^)/
今回の記事はここまでです！この記事が皆さんの役に少しでもなっていれば嬉しいです(^^)/
（参考）フーリエ変換やラプラス変換について分かりやすく解説！
以下の記事では，フーリエ変換やラプラス変換について分かりやすく解説しています！どれも無料で読めるので，興味がある方は是非読んでみてください(^^)/
