こんにちは,ハヤシライスBLOGです!今回はラプラス変換について分かりやすく解説します!
ラプラス変換について
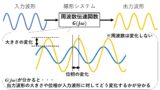
ラプラス変換とは,時間の関数を周波数の関数に変換することで,線形な微分方程式や線形なシステムの出力を,簡単に計算する方法です(^^)/
フーリエ変換ではダメか?
同じく,時間の関数を周波数の関数に変換する方法として,フーリエ変換があります!それでは,フーリエ変換で周波数領域に変換したらいいのでは?と思われる方がいるかもしれませんが,フーリエ変換にはフーリエ変換できるための条件があり,これがラプラス変換が必要になってくる理由になります(^^)/
(参考)フーリエ変換,フーリエ級数展開について分かりやすく解説!
以下の記事では,フーリエ変換やフーリエ級数展開について分かりやすく解説しています!どれも無料で読めるので,興味がある方は是非読んでみてください(^^)/

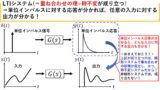
フーリエ変換→絶対可積分でない信号は,周波数領域に変換できない
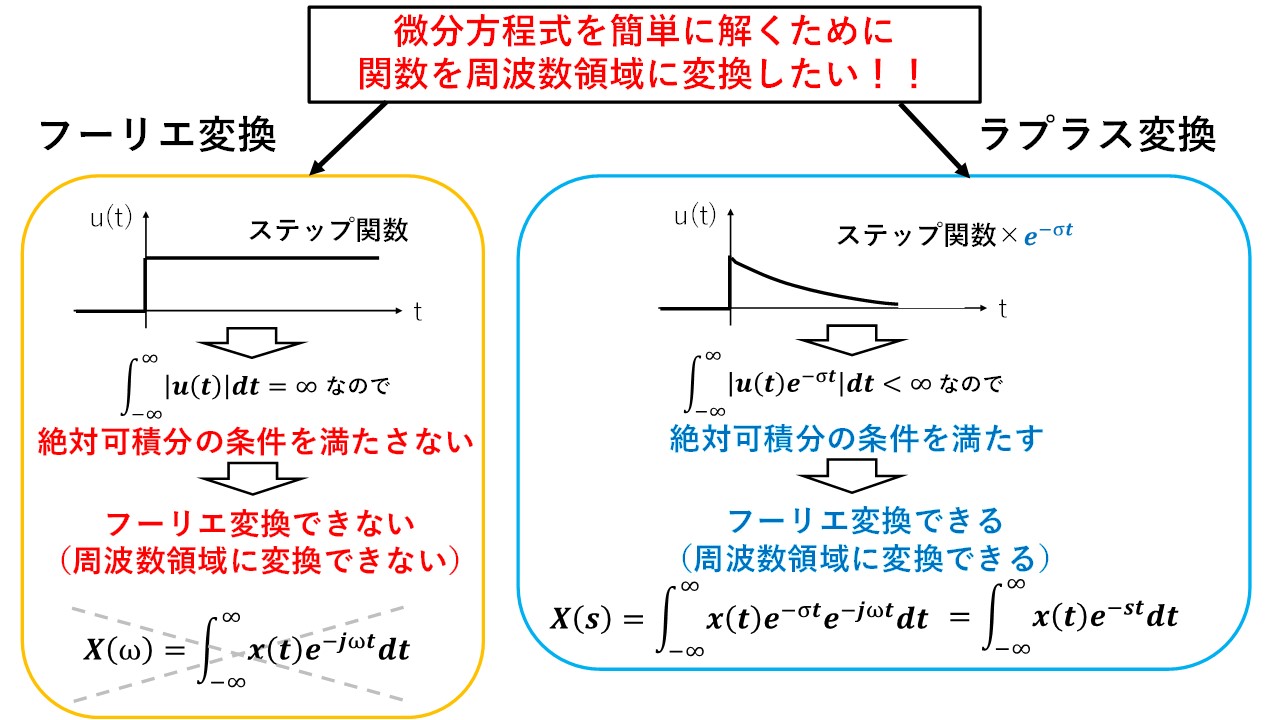
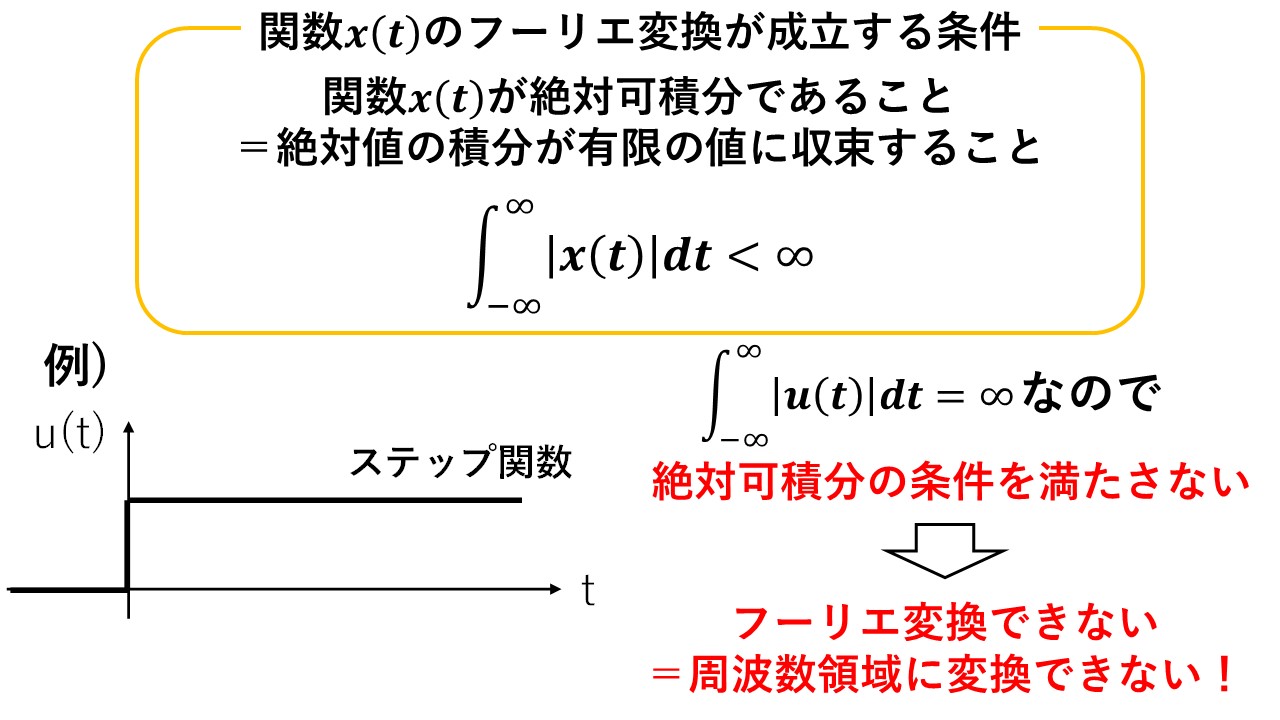
普段はあまり気にしていないかもしれませんが,そもそも関数x(t)のフーリエ変換X(ω)を求めるためには,条件がつきます! それはx(t)が絶対可積分の条件を満たすことです!要するに,何かの関数をフーリエ変換したい場合は,その関数の絶対値を[-∞~∞]の範囲で積分したときに,有限の値に収束する必要があります!しかし,下図のステップ関数のように,絶対可積分の条件を満たさない関数は結構あります(汗)
そのため,このままだと絶対可積分でない信号に対しては,周波数領域に変更できず,頑張って時間領域でガリガリ解くしかなくなってしまいます(汗) そこで登場するのがラプラス変換です!
ラプラス変換→絶対可積分でない信号も,周波数領域に変換できる
ラプラス変換とは,関数x(t)にe^(-σt)を乗じた信号をフーリエ変換したものです! e^(-σt)は,時間が経つごとに0に減衰していく信号なので,これを関数x(t)に乗じることで,絶対可積分の条件を満たすことができます!こうしてラプラス変換により,絶対可積分でない信号に対しても,周波数領域に変換できるわけですね(^^)/
ラプラス変換の公式
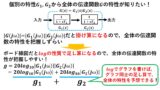
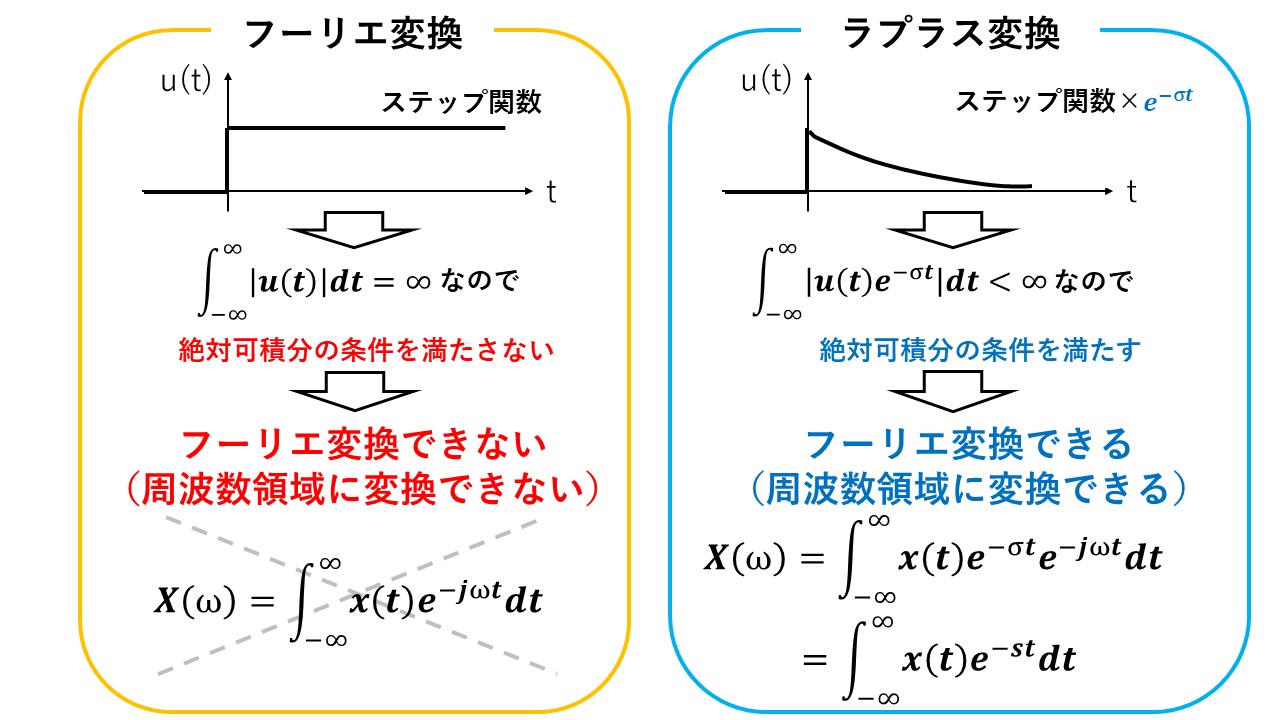
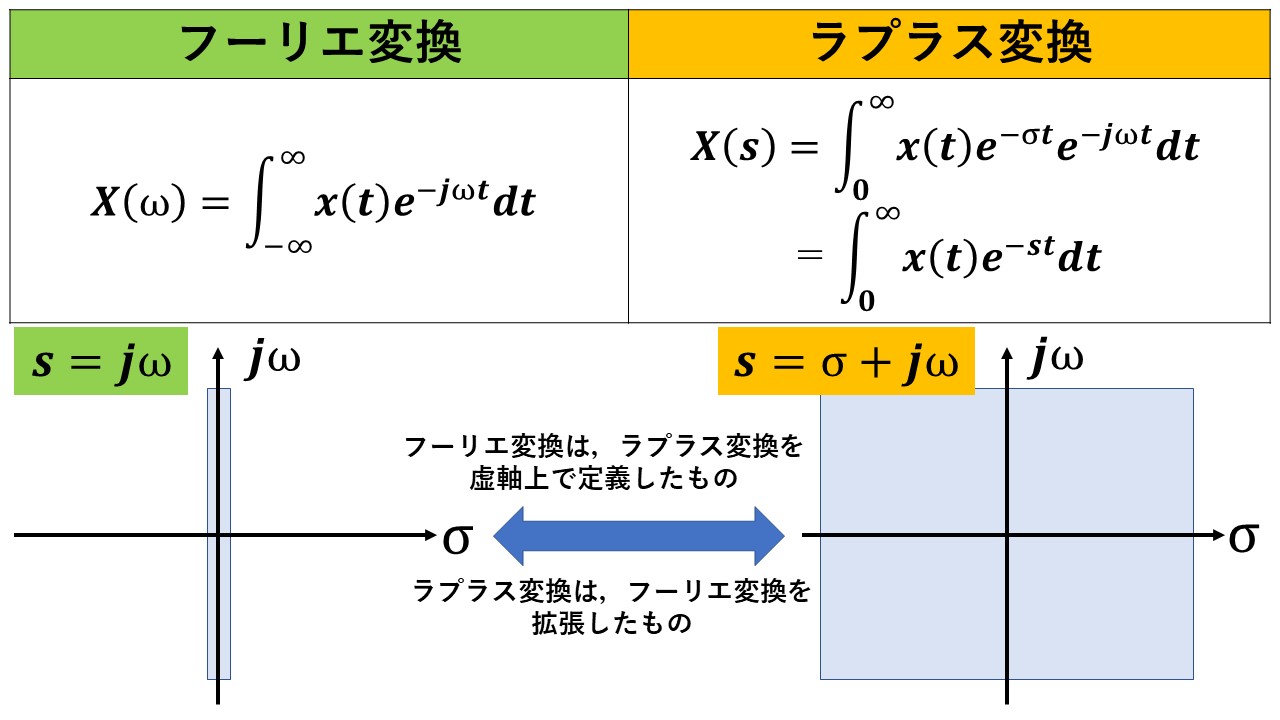
ラプラス変換とフーリエ変換の公式は,下図の通りです。ラプラス変換とフーリエ変換の違いは,関数x(t)にe^(-σt)が乗じられている点のみであることが分かりますね(^^)/
また,ラプラス変換の複素数s=σ+jωのσを0とすればフーリエ変換になります!このことから,フーリエ変換はs平面上の虚軸で定義したラプラス変換であるといえます!
今回の記事はここまでです!少しでも役に立っていれば嬉しいです(^^)/
(参考)システム制御工学について分かりやすく解説!
以下の記事では,システム制御工学に関する内容について分かりやすく解説しています!どれも無料で読めるので,興味がある方は是非読んでみてください(^^)/