こんにちは，ハヤシライスBLOGです！今回はフーリエ解析の概要と，フーリエ解析の基礎となるフーリエ級数展開について，できるだけ分かりやすく解説します！
フーリエ解析の概要
フーリエ解析とは，図1のように信号や波形の中にどんな周波数成分が含まれているかを分析する方法です！
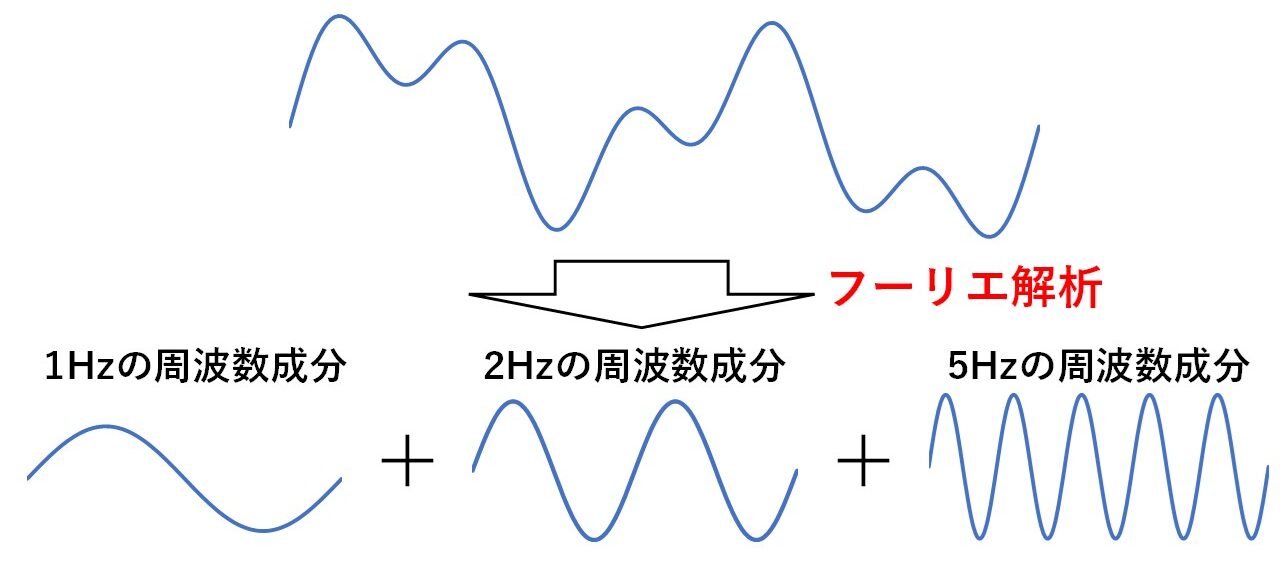
図1 フーリエ解析のイメージ
フーリエ解析の種類
図2のように，フーリエ解析では周波数を分析したい信号や波形が，①デジタル信号（値がとびとびの離散的な信号）なのかアナログ信号（値が連続的な信号）なのか，②周期性があるかないかによって，使用する手法が変わります！
例えば，この記事で説明するフーリエ級数展開は，アナログ周期信号にどんな周波数が含まれるかを知りたい場合に使用する方法になります！アナログ非周期信号に含まれる周波数成分が知りたい場合は，フーリエ変換を使います！
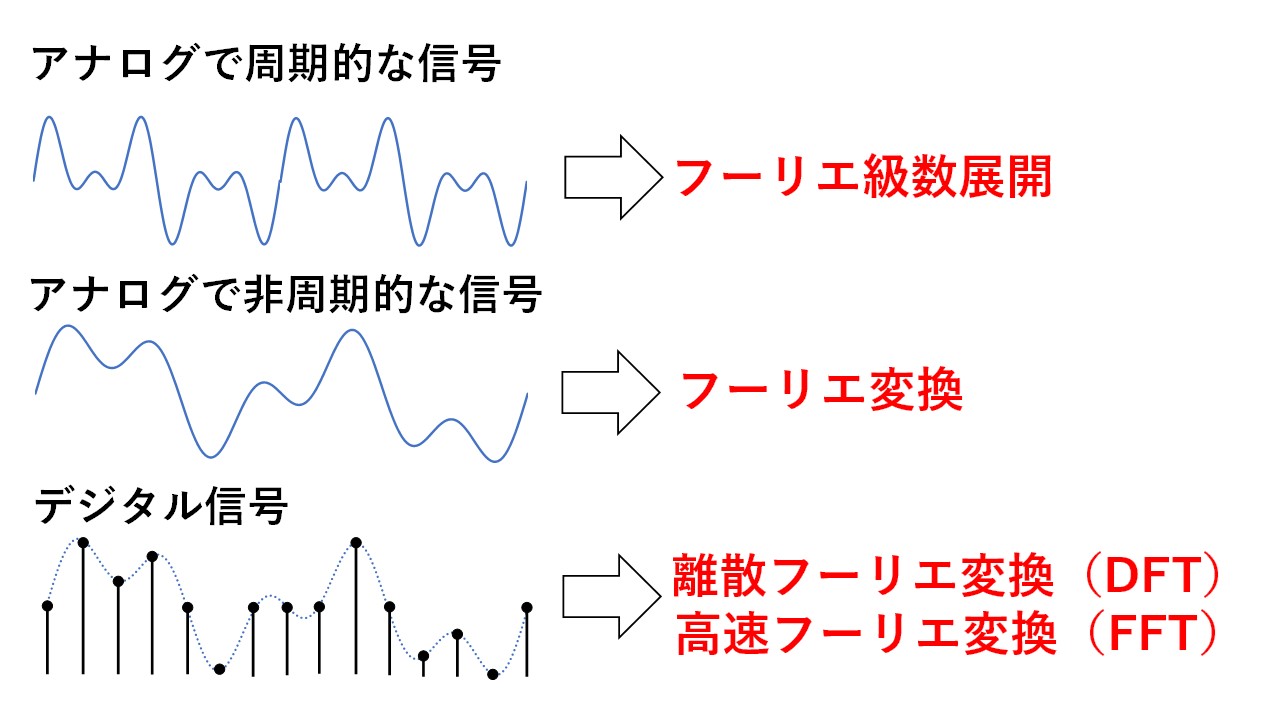図2 フーリエ解析の種類
フーリエ変換については，以下の記事で分かりやすく解説していますので是非参考にしてください(^^)/
フーリエ級数展開の概要
フーリエ解析の基礎となるのが，実はフーリエ級数展開になります！以下では，フーリエ級数展開の概要について説明します！
フーリエ級数展開とは，図3のように周期的なアナログ信号（連続的な波形）に，どんな周波数成分がどんな大きさで含まれているかを知りたいときに，使用する手法です！
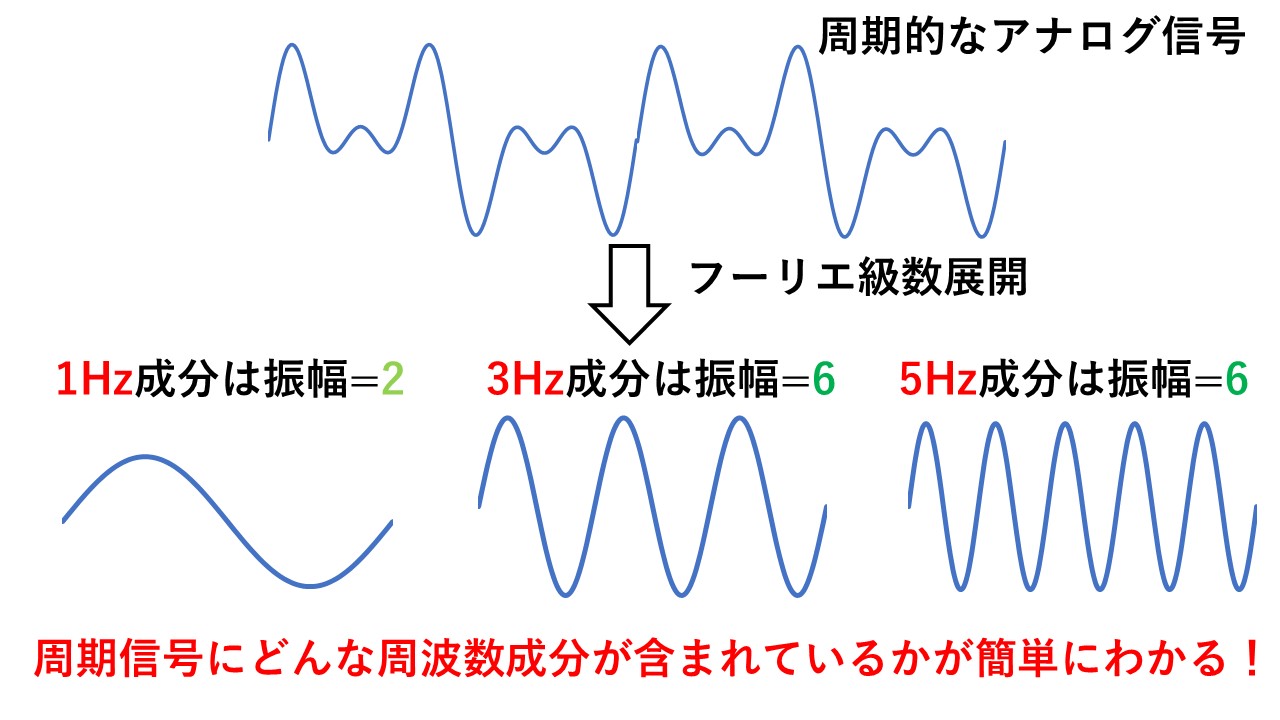図3 フーリエ級数展開のイメージ
フーリエ級数展開の式
以下では，フーリエ級数展開でどのようにして元の信号に含まれる周波数成分が分かるのかを説明します！
周期的な連続信号x(t)の周期をT秒とすると，図4のようにx(t)はフーリエ級数展開により色々な周波数の三角関数の無限和としてあらわすことができます！そして，amやbm等はフーリエ係数と呼ばれ，図5の公式で求めることができます！
図4 フーリエ級数展開の式
図5 フーリエ係数を求める公式
ここで重要なことは以下の2つです！
①目的は周期信号x(t)にどんな周波数成分がどんな大きさで含まれているかを知ることであり，それはa0～am、b1～bm等のフーリエ係数さえ求まれば，全部分かる！
②フーリエ係数は，図5のように色々な周期のsinあるいはcosを周期信号x(t)にかけて積分するだけで，簡単に求めることができる！
①については，例えばbのフーリエ係数が全部0で，aの係数についてはa1=1，a2=5でそれ以外は全て0と分かった場合，元の信号x(t)は周期T[s]で大きさ1の周期成分と，周期T/2[s]で大きさが5の周期成分から成るというのが分かります！このようにフーリエ係数さえ分かってしまえば，元の周期信号にどんな周波数成分がどんな大きさで含まれているかを把握することができます(^^)/
②については，これがフーリエ級数展開のポイントになります！なぜsinやcosを元の信号にかけて積分するだけで簡単にフーリエ係数を求めることができるのでしょうか？以降で詳しく解説します(^^)/
フーリエ係数を求める公式の解説
ここでは，なぜフーリエ係数を簡単に求めることができるかを解説します！最初に答えを言ってしまうと，その秘密は三角関数の直行性にあります(^^)/
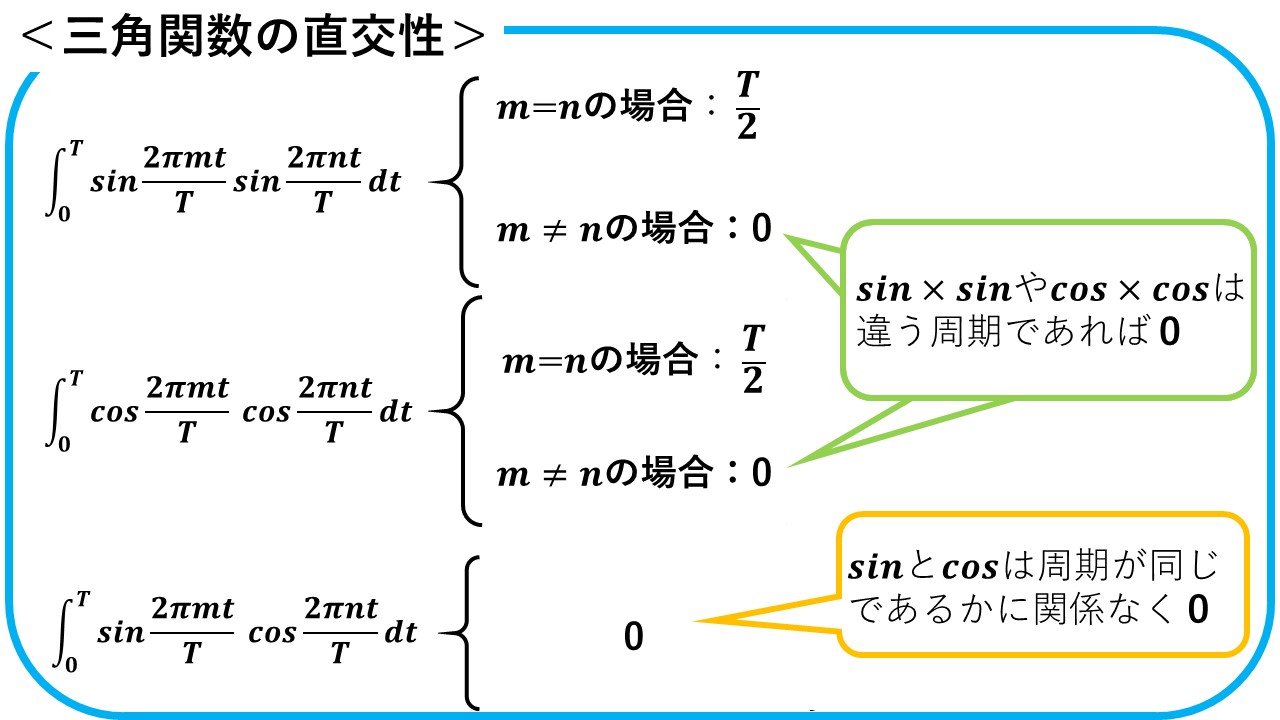
三角関数の直交性
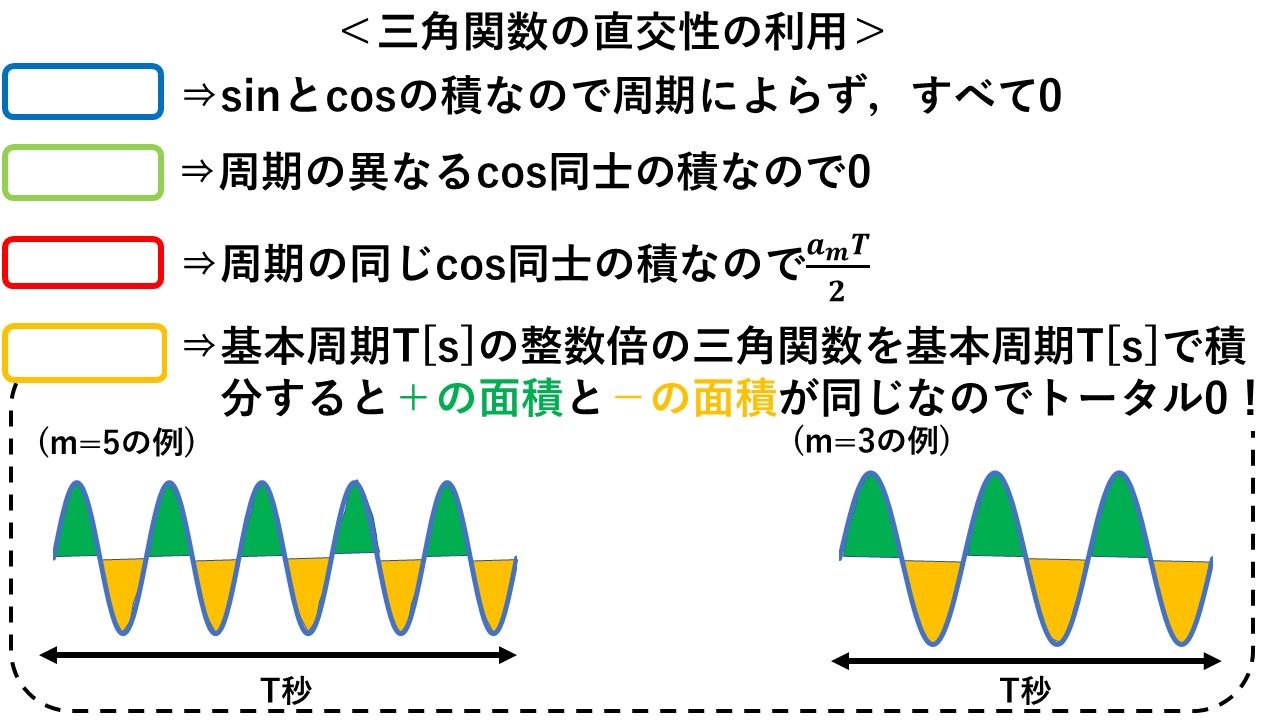
三角関数の直交性について，ここでは結果だけを示します！ 要するに，sin同士の積の積分やcos同士の積の積分は周期が同じでない限り0となり，sinとcosの積の積分は周期が同じかどうかによらず0になるというものです！これが，フーリエ係数を求める時に，絶大な威力を発揮します！
図6 三角関数の直交性
フーリエ係数の公式の導出
それでは，三角関数の直交性をどのように利用してフーリエ係数を求めることができるのかを，周波数m/T[Hz]（＝基本周波数1/T[Hz]のm倍成分)のフーリエ係数amを例に解説します！
まず分析する信号x(t)に，求めたいフーリエ係数amに対応する周期のcos成分（＝cos(2πm/Tt)）をかけます！ x(t)は色々な周波数成分の三角関数の和で表されるはずですから，x(t)にcos(2πm/Tt)をかけた式は，以下になります！
なお，上の例ではフーリエ係数amが知りたいのでcos(2πmt/T)をかけていますが，もしa3が知りたければcos(2π3t/T)をかけますし，bmが知りたい場合はsin(2πmt/T)をかけます(^^)/
次に，両辺を周期T[s]の区間で積分します
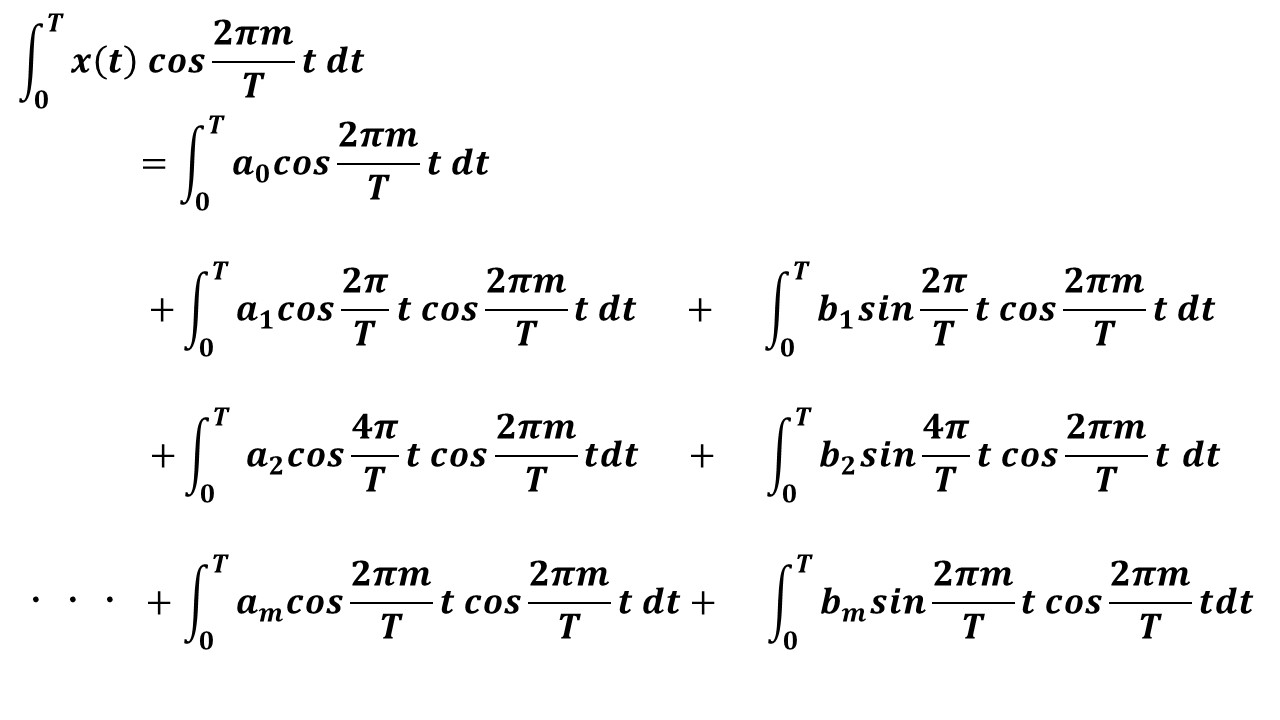
続いて，三角関数の直交性を利用します(^^)/ a0，a1，・・・やb1，b2など，am以外のフーリエ係数の項は，三角関数の直交性により，いずれも0になって消えてしまうのが分かりますね(^^)/ その結果，求めたかったフーリエ係数amの項だけが残ります！
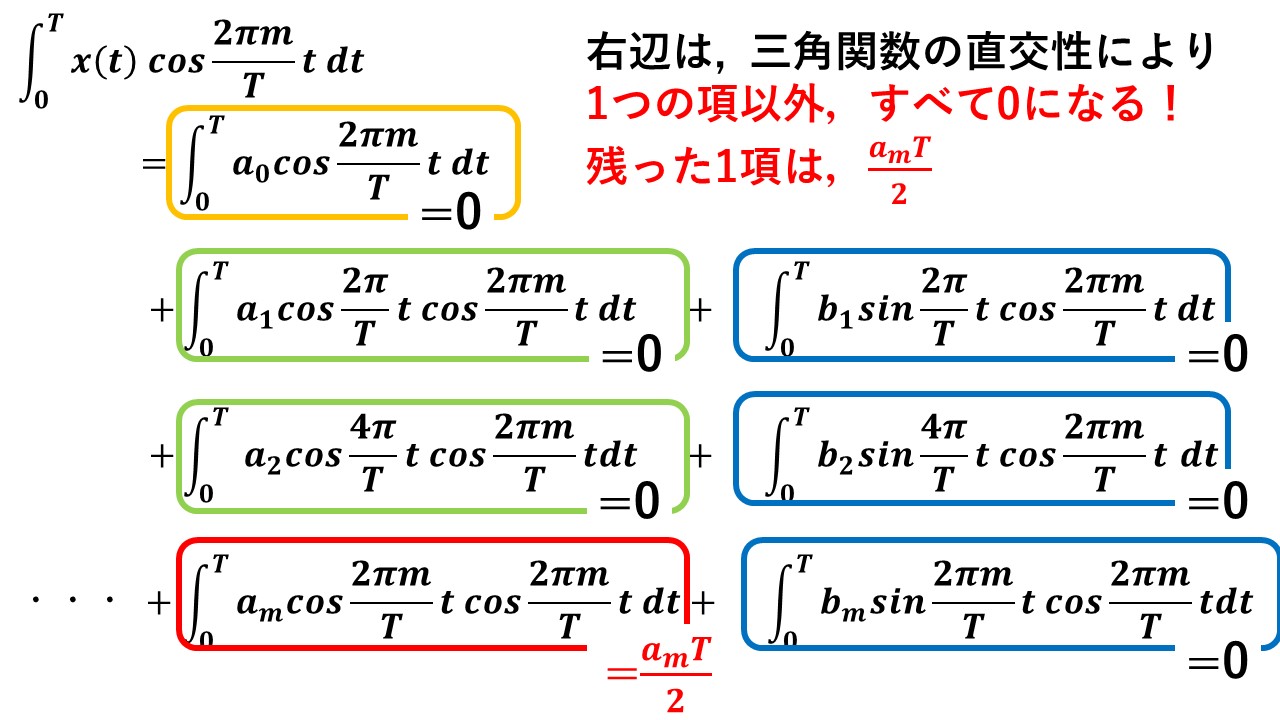
最後にam=の形に変形すると，フーリエ係数amを求めることができます！つまり，三角関数の直行性を利用すれば，求めたいフーリエ係数に関係のない項が全部0になって消えてしまう訳ですね(^^)/ このおかげで，求めたいフーリエ係数を簡単に計算することができます！
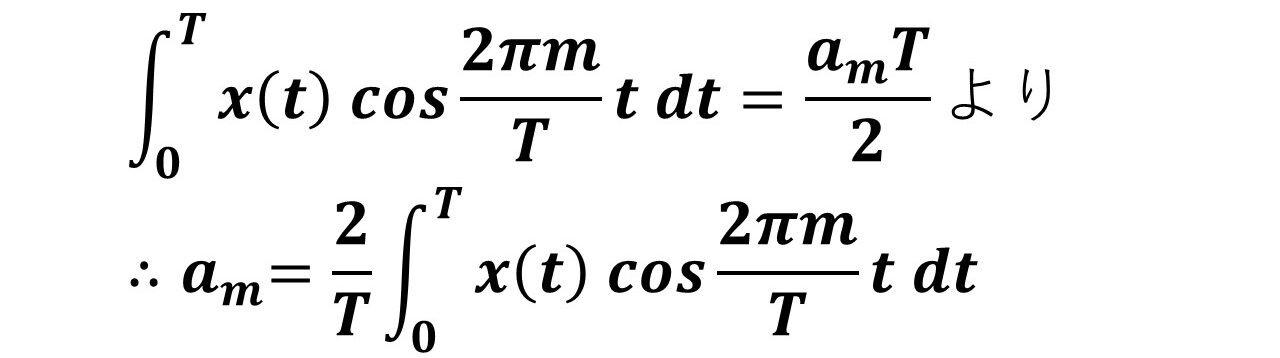
なお，今回の例ではamを求めましたが，三角関数の直行性を利用すれば，am以外のaのフーリエ係数やbのフーリエ係数も同じ方法で導くことができます！
フーリエ級数展開のまとめ
以上をまとめると，以下の通りです！
-
- フーリエ級数展開を用いた周波数分析とは，周期的なアナログ信号にどんな周波数成分がどんな大きさで含まれているかを把握する手法である！
- 周期信号に含まれる周波数成分は，フーリエ係数が求まれば全部分かる！そして，それらのフーリエ係数は三角関数の直行性を利用することで，簡単に求めることができる！
フーリエ変換について分かりやすく解説
以下の記事では，フーリエ変換について分かりやすく解説しています！フーリエ級数展開との違い等を分かりやすく解説していますので，もし気になった方は是非読んでもらえると嬉しいです(^^)/
