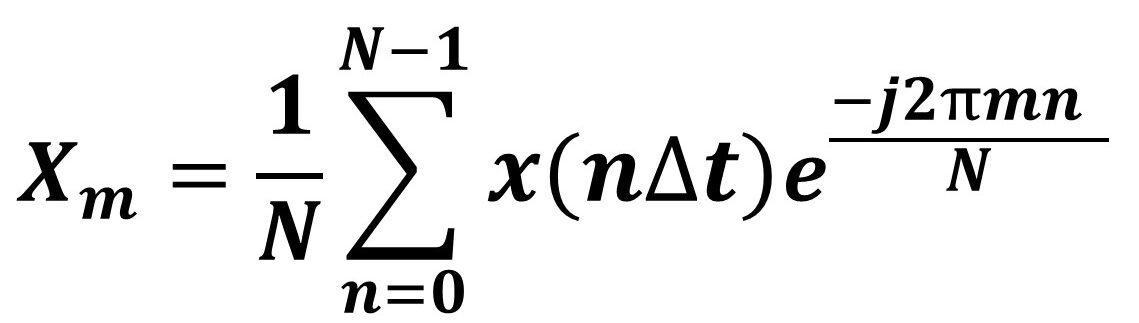こんにちは，ハヤシライスBLOGです！今回は，離散フーリエ変換を使って振幅スペクトルを求める場合の注意点について，主に振幅スペクトルの大きさと実際の振幅の関係に着目して解説します(^^)/
離散フーリエ変換(DFT：Discrete Fourier Transform)とは？
離散フーリエ変換とは，実験等で得られるデジタルの計測データに，どんな周波数成分がどんな大きさで含まれているのかを調べる際に使う手法で，以下の式で求めることができます(^^)/
離散フーリエ変換の式
DFTにより振幅スペクトルから実際の振幅を求める場合の注意点
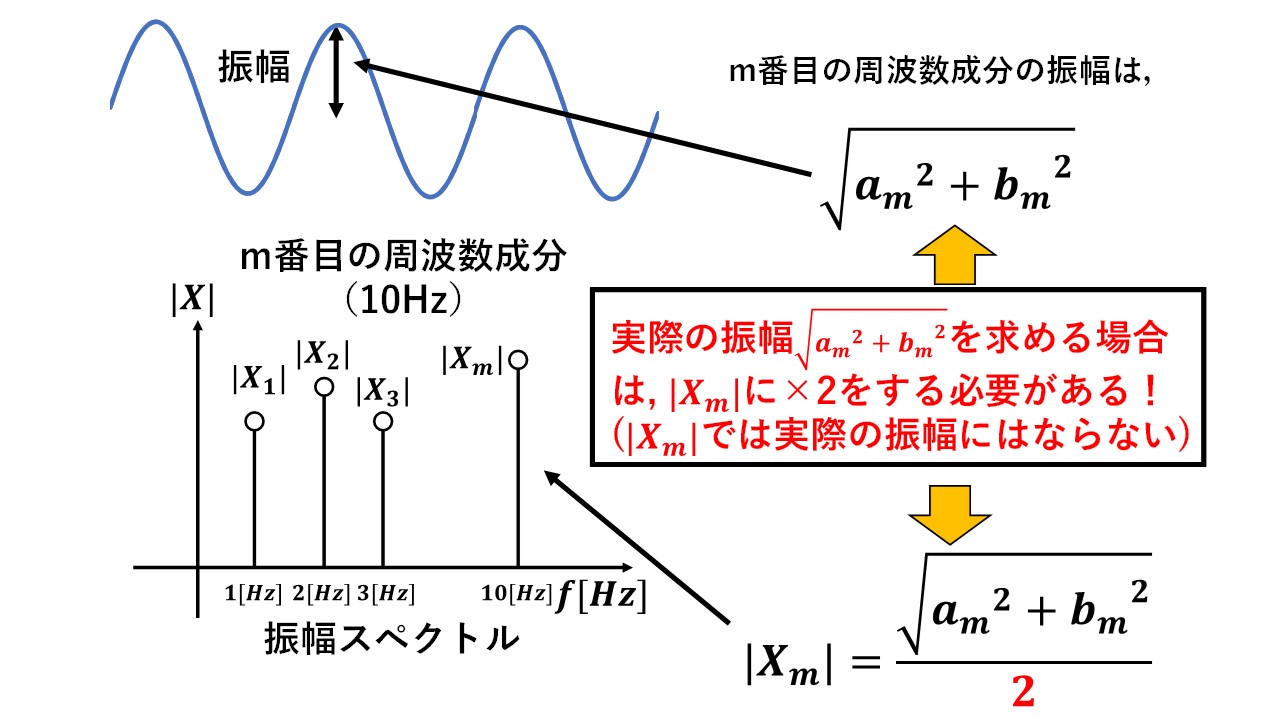
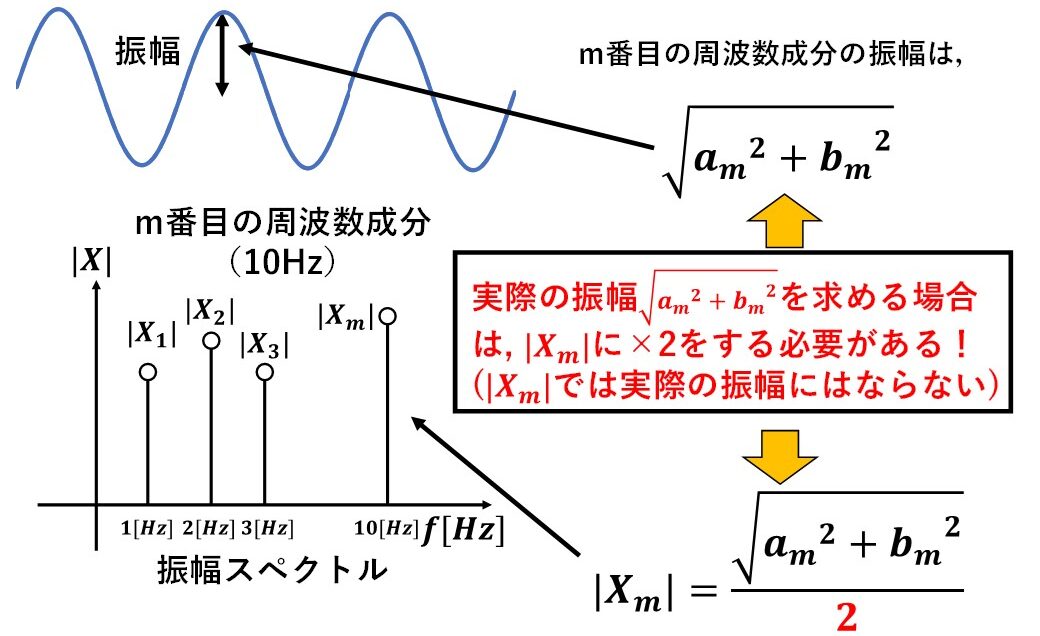
計測したデジタル信号にどんな周波数成分が含まれるかだけを知りたい場合は，特段意識する必要はありませんが，その周波数成分の振幅まで知りたい場合は注意が必要です！よくある間違いは，以下の通り，振幅スペクトルの大きさ|Xm|=実際の振幅としてしまうことです(^^)/ 結論から言ってしまうと，実際の振幅は|Xm|ではなく，2×|Xm|により求めることができます！以下で，順を追って解説します(^^)/
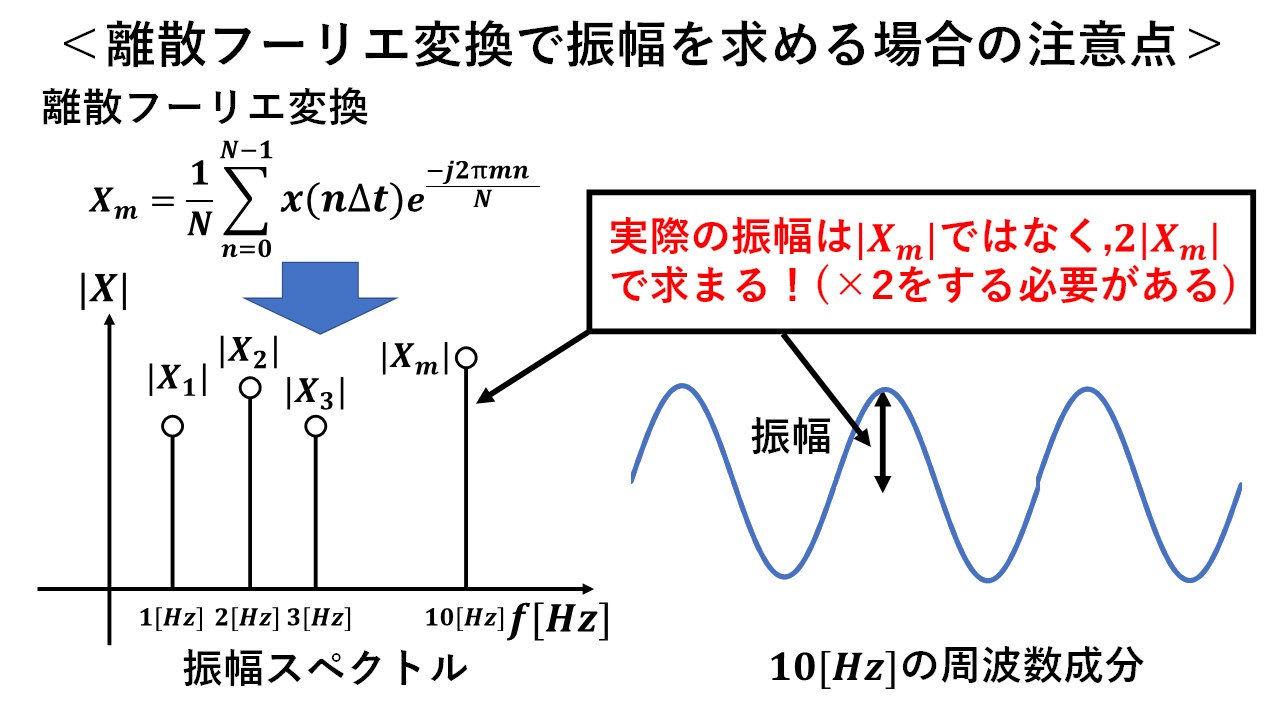図1 DFTにより振幅スペクトルから実際の振幅を求める場合の注意点
そもそもDFTは，複素フーリエ級数展開をデジタルデータ用に拡張したもの
まず離散フーリエ変換の式の大本の式をおさらいしましょう！以前別の記事で解説しましたが，離散フーリエ変換は，アナログ信号に対して使う複素フーリエ級数展開の式を，離散データ（デジタルデータ）に適用できる形にしたものでした(^^)/ したがって，複素フーリエ級数展開の式を紐解けば，なぜ実際の振幅を求める場合に，わざわざ|Xm|に対して×2をする必要があるのかが分かりそうですね！以下では複素フーリエ級数展開の式を使って，順を追って説明します(^^)/ なお，離散フーリエ変換の理解がまだの方は，是非以下の記事を確認してみてください！
図2 離散フーリエ変換の成り立ち
（参考）フーリエ変換やフーリエ級数展開を0から理解したい方にオススメの書籍
なお，フーリエ変換や（複素）フーリエ級数展開など，フーリエ変換全般を0から理解したい方は，以下の書籍がものすごくオススメです！今回の記事の基礎となるフーリエ級数展開やフーリエ変換について，数学的にも分かりやすく説明されていますし，デジタルな信号を扱う際に必要な知識がギュッと詰まっています(^^)/ 著者もフーリエ変換に関連した本の中では，この本が断然オススメです(^^)/ 初めて読んだ時，その分かりやすさに感動しました！是非，読んでみてください(^^)/
まず実際の振幅を求めてみよう
今，元の信号x(t)が図3の通り，様々な三角関数の和で表されるものとします。今，はじめから数えてm番目の周波数成分（つまり，基本周波数1/T[Hz]のm倍であるm/T[Hz]の成分）に着目すると，その振幅はm番目の周波数のcos成分の大きさとsin成分の大きさの合成で求まりますから，cos成分の大きさをam，sin成分の大きさをbmとすると，求めたい振幅は√(am^2+bm^2)になります(^^)/
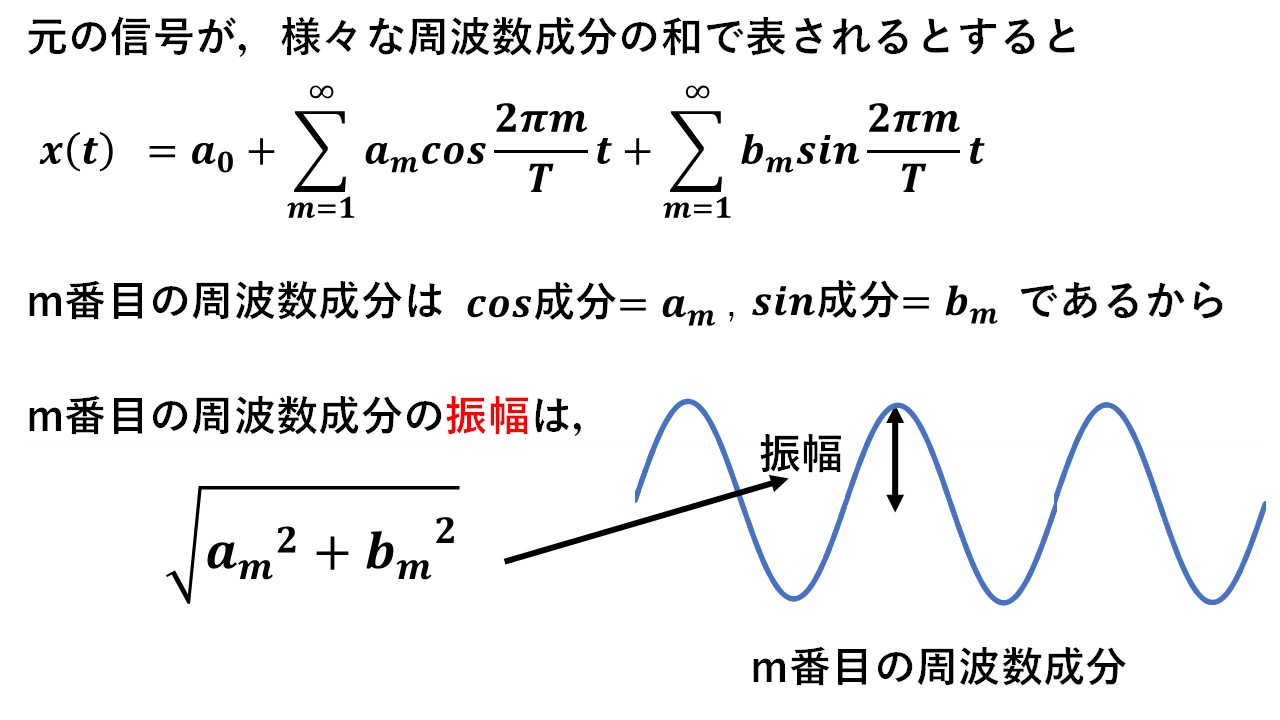図3 m番目の周波数成分(m/T[Hz]成分)の振幅の大きさ
|Xm|を計算してみよう
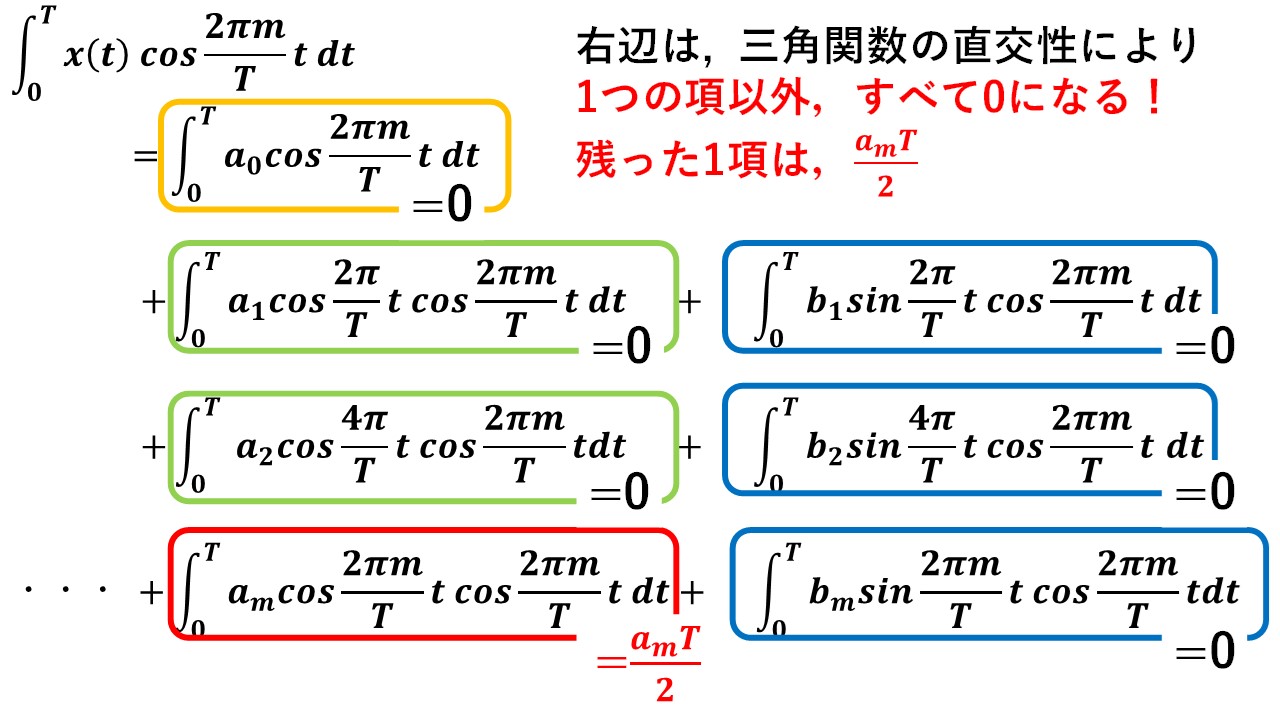
続いて，|Xm|を計算してみましょう！ オイラーの式を使って整理すると，複素フーリエ級数展開の式Xmは，以下の図4の通り，cosを含んだ項とsinを含んだ項の2つに分解できます ここで，図5に示した通り三角関数の直行性を用いると，sinとcosの積の積分や，周期が同じ出ないsin同士 or cos同士の積の積分はいずれも0になりますから，結果的にXmはamとbmを使って，Xm=am/2-jbm/2と表されます！したがってその大きさ|Xm|は√(am^2+bm^2)÷2と表されます(^^)/この÷2が非常に重要ですので覚えておきましょう！
なお，図5を見て理解がいまいちの方は，以下の記事でもう少し詳しく解説していますので，是非参考にしてください(^^)/
図4 |Xm|の計算
図5 三角関数の直行性を利用した計算
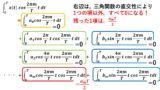
実際の振幅 ＝ |Xm|×2になる理由 （×2をする理由）
図6に，実際の振幅と|Xm|の比較結果を示します！実際の振幅が√(am^2+bm^2)で表されるのに対し，|Xm|は√(am^2+bm^2)÷2になっていることが分かります(^^)/ したがって，実際の振幅を求める場合には，|Xm|に×2をしてあげないと，実際の振幅にはならないことが分かります！！ これが，振幅スペクトルから実際の振幅を求める場合の注意点になります！
結局のところ，Xm=am-jbmになればこのような問題は発生しなかったのですが，Xm=(am-jbm)÷2になっていることが，今回の原因になっていたのでした(^^)/ 振幅スペクトルを使ってその大きさを求める場合には，注意しましょう！！
図6 実際の振幅と|Xm|の比較
今回の記事はここまでです！お疲れ様でした(^^)/
（参考）フーリエ変換，ラプラス変換を分かりやすく解説！！
以下の記事では，フーリエ変換，ラプラス変換などについても分かりやすく解説しています！どれも無料で読めるので，興味がある方は，是非読んでみてください！
