こんにちは,ハヤシライスBLOGです!今回はボード線図の特徴やメリットについて分かりやすく解説します!
周波数伝達関数のゲイン特性・位相特性 (復習)
ボード線図の話をする前に,まずは周波数伝達関数について復習しましょう!
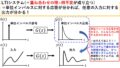
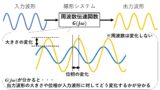
図1のように,線形システムに正弦波を入力すると,振幅の大きさや位相が変化して出力されます!この時,伝達関数が単純なゲインであれば,どんな周波数の正弦波を入力しても振幅の変化が一定なので,出力波形を予想するのは簡単ですが.実際は入力する正弦波の周波数によって,振幅や位相の変化の仕方が変わります!この変化の仕方を一目見て分かるのが,図2の周波数伝達関数から書いたゲイン特性,位相特性でした(^^)/
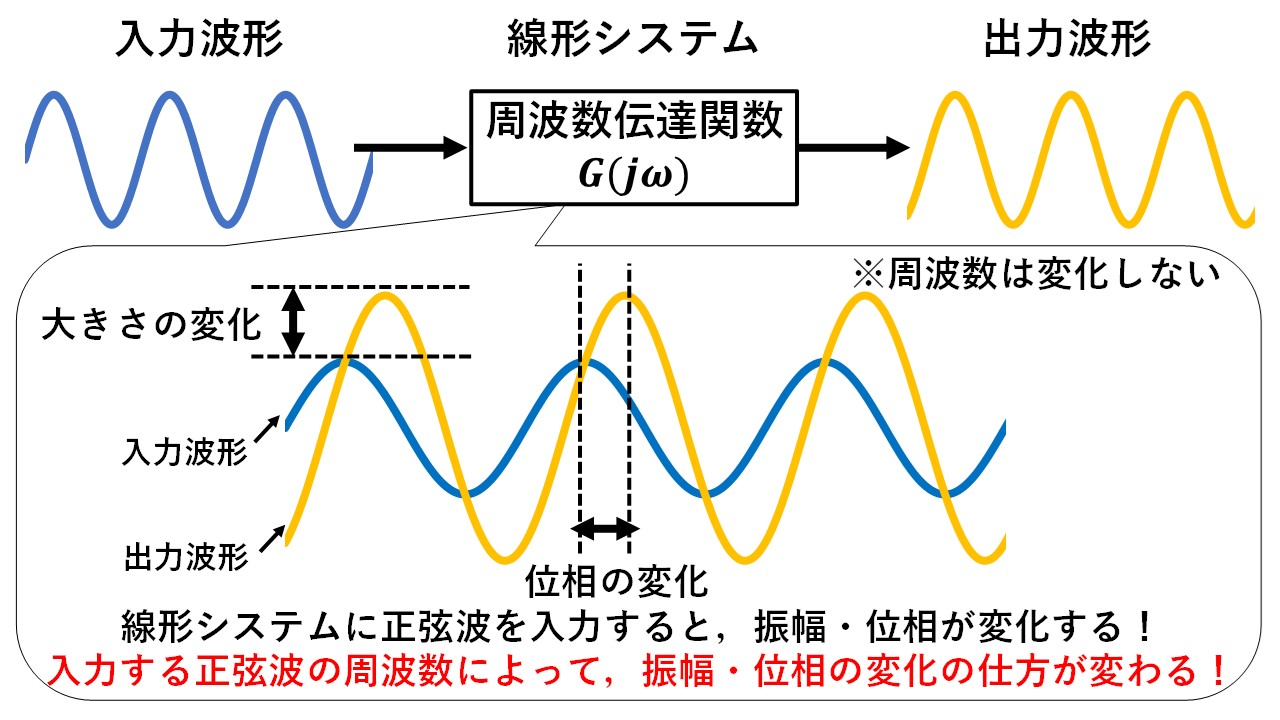 図1 線形システムの入力波形と出力波形
図1 線形システムの入力波形と出力波形
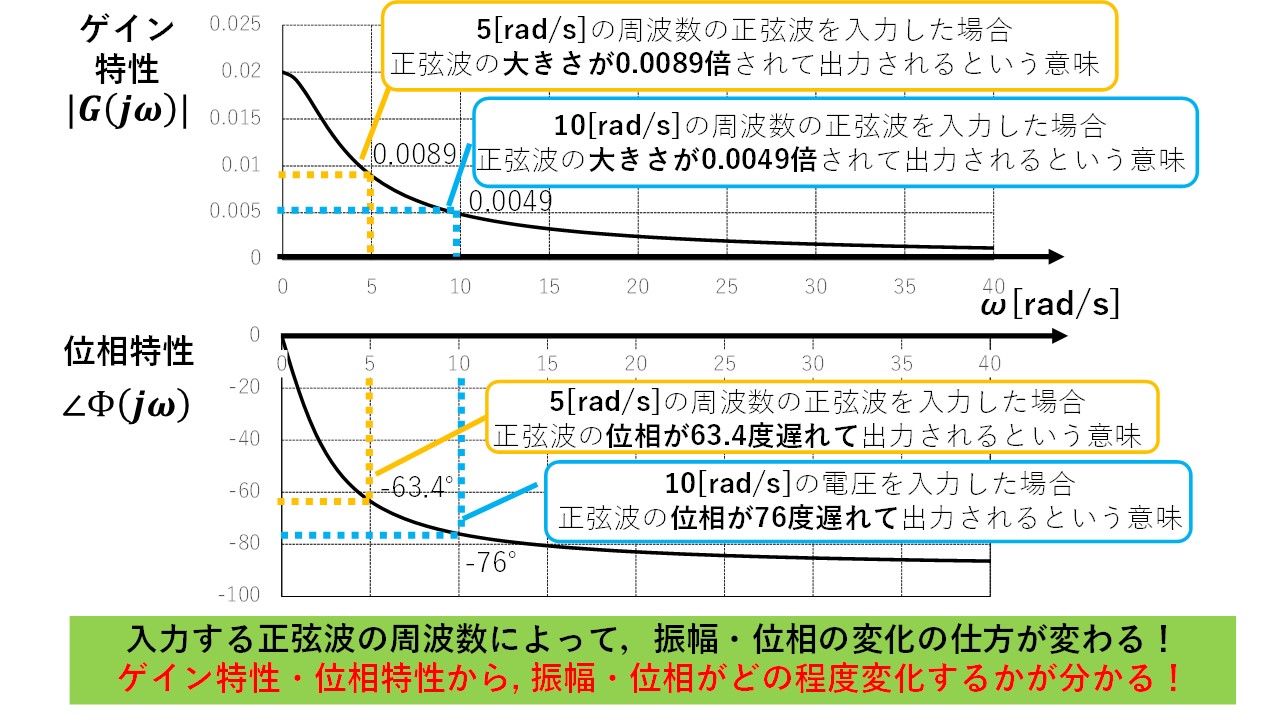 図2 ゲイン特性・位相特性の例
図2 ゲイン特性・位相特性の例
なお,周波数伝達関数のメリット等については,以下の記事で解説しております!初めての方でも分かりやすいように解説していますので,良かったら参考にしてください(^^)/
ボード線図とは
ボード線図とは,図2と同じでシステムのゲイン特性,位相特性を表すものですが,ゲイン特性の縦軸が単なる|G|ではなく,図3のようにlogがとられています!この理由は,図を見やすくしたり,考察を簡単にできるようにするためなのですが,なかなか初見で理解するのは大変ですので,一つずつ見ていきましょう!
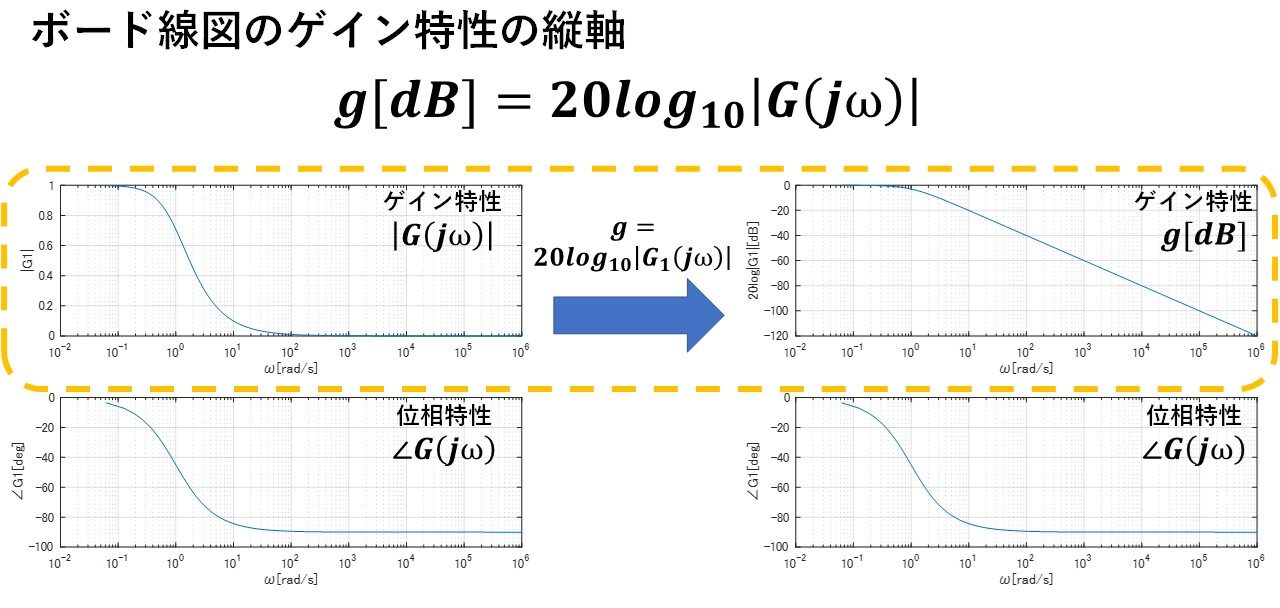 図3 ボード線図とは
図3 ボード線図とは
以下では,ボード線図の特徴について解説しますが,これを説明するためには対数関数logの性質を把握しておく必要があるので,まずlogの最低限の公式だけ復習して,その後ボード線図の特徴について解説します!
対数関数logの重要な性質
図4の通り,対数関数logの重要な点は,かけ算はlogをとると足し算になり,わり算はlogをとると引き算になるという点です!この性質が,実はボード線図のメリットの部分に大きく関係しますので,ここでしっかりと覚えておきましょう(^^)/
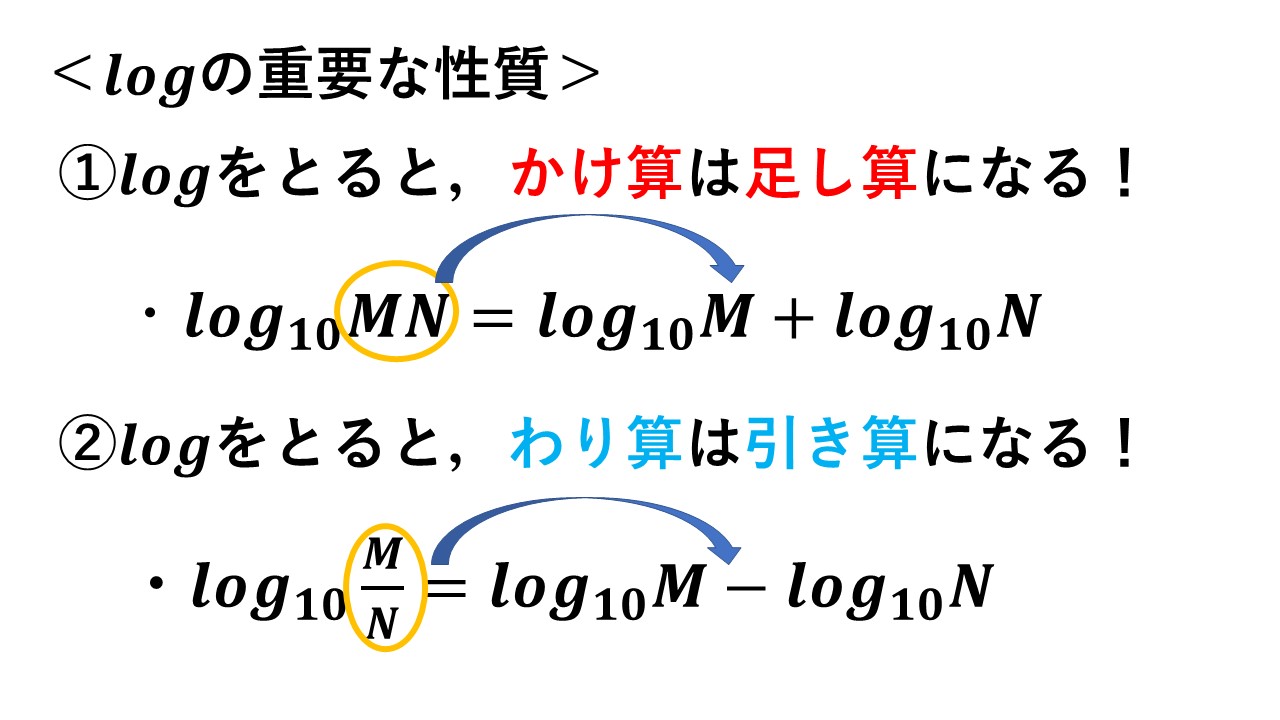 図4 対数関数logの重要な性質・公式
図4 対数関数logの重要な性質・公式
ボード線図の特徴① 縦接続の特性が簡単に分かる(^^)/
一つ目の特徴は,図4上のブロックのような縦接続(ブロック同士のかけ算)の特性が簡単に分かるというものです(^^)/ 実は,この特徴こそが,ボード線図を考える最大のメリットになります!
結論から言ってしまうと,制御ブロックというのは,縦接続(ブロック同士のかけ算)になる場合が非常に多いのですが,ボード線図のようにグラフの縦軸にlogをとることで,logの重要な性質である「かけ算は足し算になる」という性質をフル活用でき,個別の伝達関数の特性さえ分かっていれば,簡単に全体の特性を予想・把握できるようになります(^^)/
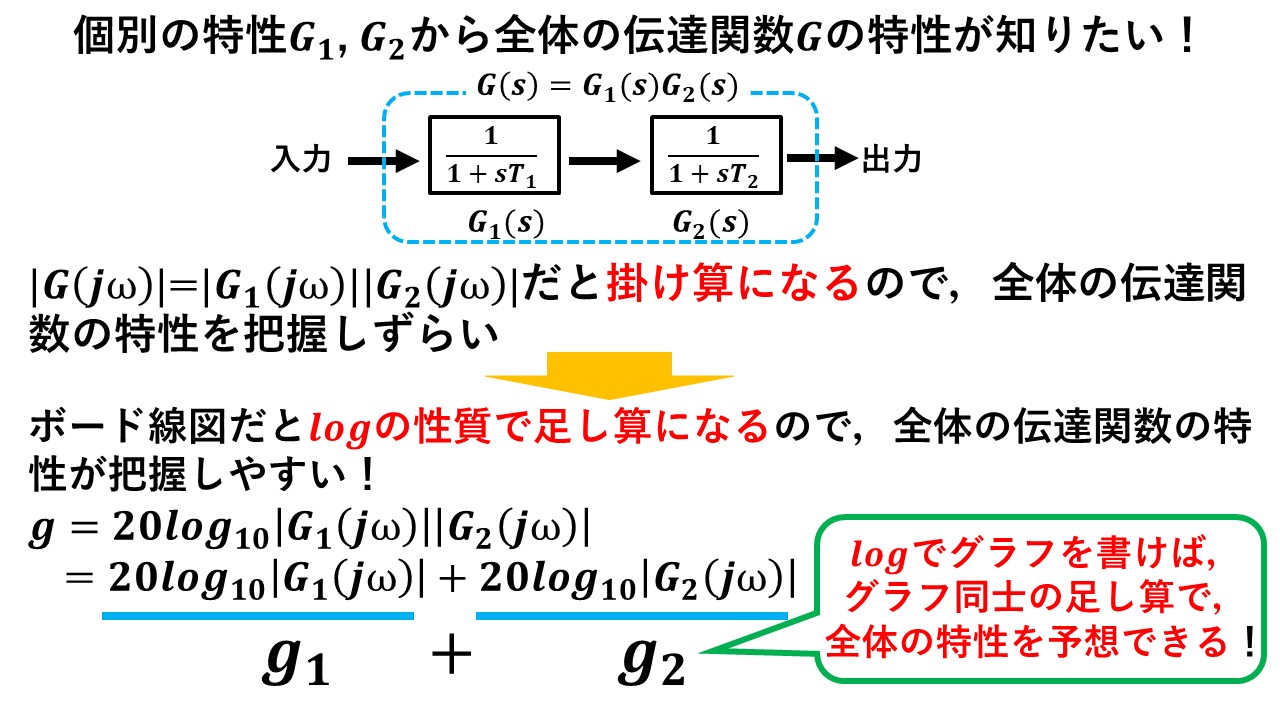 図5 ボード線図のメリット(数式編)
図5 ボード線図のメリット(数式編)
例えば図5のように,時定数の異なる2つの一次遅れのブロックがあり,各伝達関数G1,G2の特性は分かっているけど,全体の特性Gが分からないとします!
ボード線図を考えない場合,全体のゲイン特性|G|は|G1|と|G2|のかけ算になり,全体の特性を予想するのが大変です!(この例ではブロックが2つしかありませんが,ブロックが沢山あるとかなり厳しいです・・)一方で,ボード線図を考える場合,logの性質でかけ算は足し算になるため,logをとったグラフ,すなわちボード線図を書けば,個別の伝達関数のグラフの足し算で,全体の伝達関数のグラフを書くことができます(^^)/
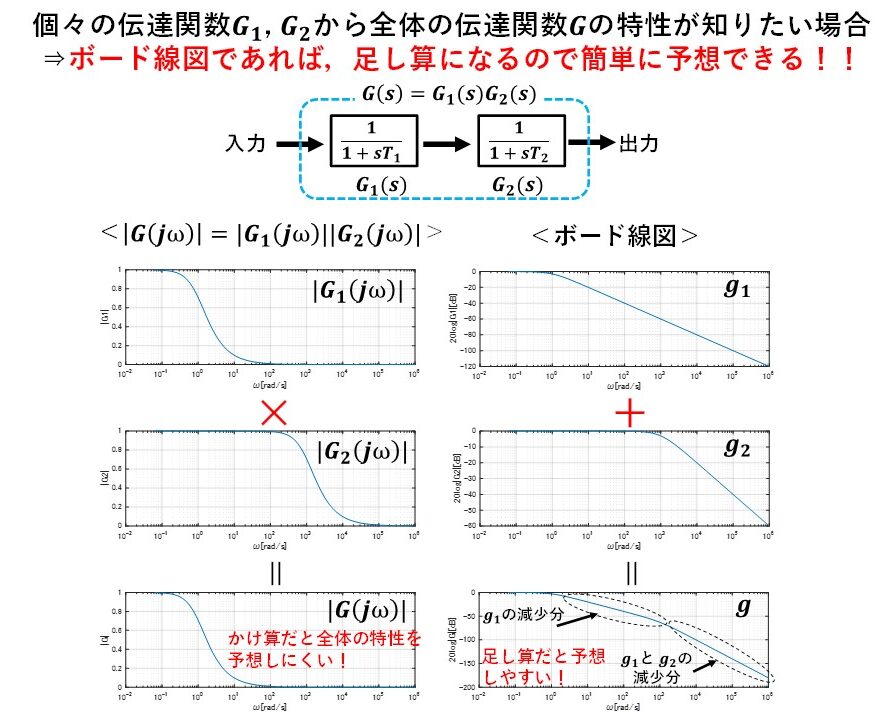 図6 ボード線図のメリット(実例編)
図6 ボード線図のメリット(実例編)
図6は,ボード線図を考えない場合と考えた場合の違いを表したグラフです!ボード線図の場合,個別の伝達関数のグラフの足し算で,全体の伝達関数のグラフを書くことができますので,簡単に全体の特性を予想できます(^^)/
ボード線図の特徴② 周波数のレンジが広くても,ゲイン特性が見やすい!
ボード線図の2つ目の特徴は,周波数のレンジが広い場合でも,全体の特性が見やすい点です!
例えば図7のような一次遅れブロック(T=1[s])のゲイン特性をボード線図を使わずに書いた場合,周波数が高い領域においても縦軸の値はけっこう変化しているのですが,縦軸のレンジが広いため,周波数が低い領域の変化しかグラフからは読み取ることができません!一方で,ボード線図の場合,周波数が10倍,100倍されても縦軸は20[dB]ずつしか変化しないため,周波数のレンジが広い場合でも,ゲイン特性の変化が非常に見やすいことが分かるかと思います(^^)/
ちなみに,ボード線図において,なぜωを10倍,100倍にした時にゲインが20dBずつしか変化しないのかを,図7の右で説明しています!要するに,ωが10倍,100倍されるとωの係数に10や100が付き,これがlogの性質「かけ算は足し算」により分離され,それに20がかけ算されるので,20dBずつ変化します(^^)/
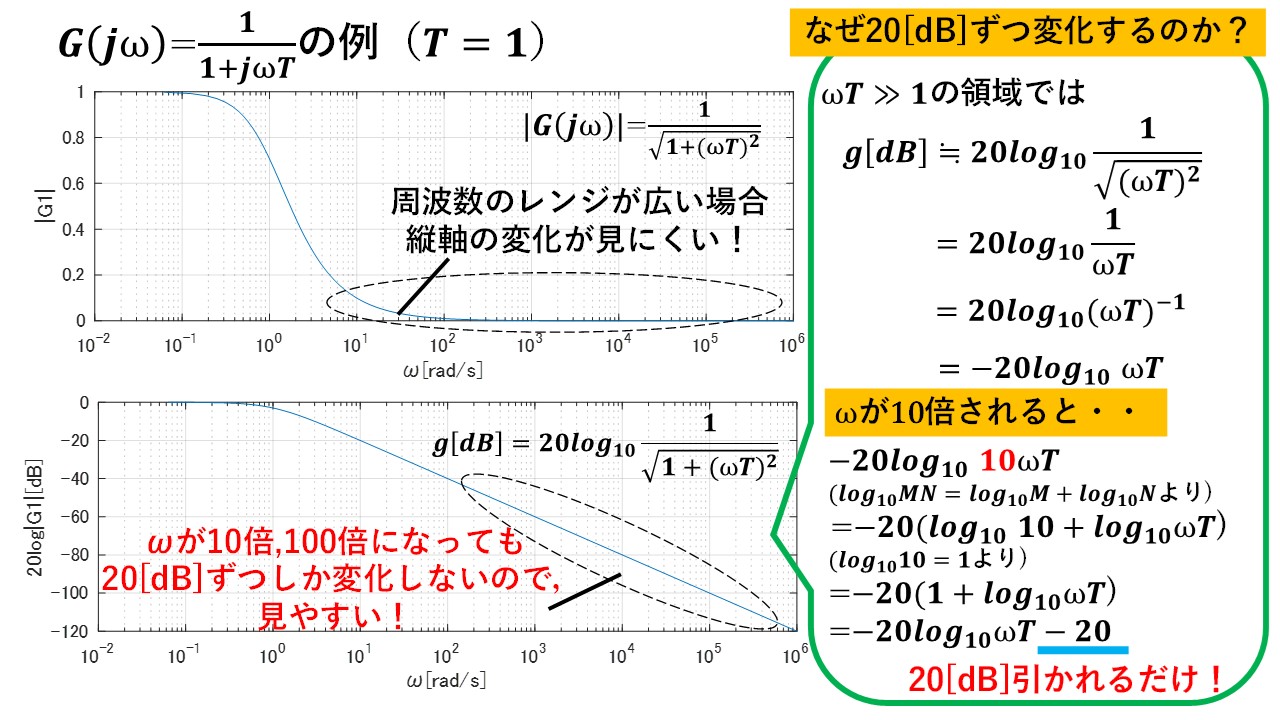 図7 ボード線図の見やすさ
図7 ボード線図の見やすさ
今回の記事はここまでです!少しでも皆さんの役に立っていれば嬉しいです(^^)/