こんにちは，ハヤシライスBLOGです！今回はフーリエ解析の概要と，フーリエ変換について，できるだけ分かりやすく解説します！
フーリエ解析の概要
フーリエ解析とは，図1のように信号や波形の中にどんな周波数成分が含まれているかを分析する方法です！
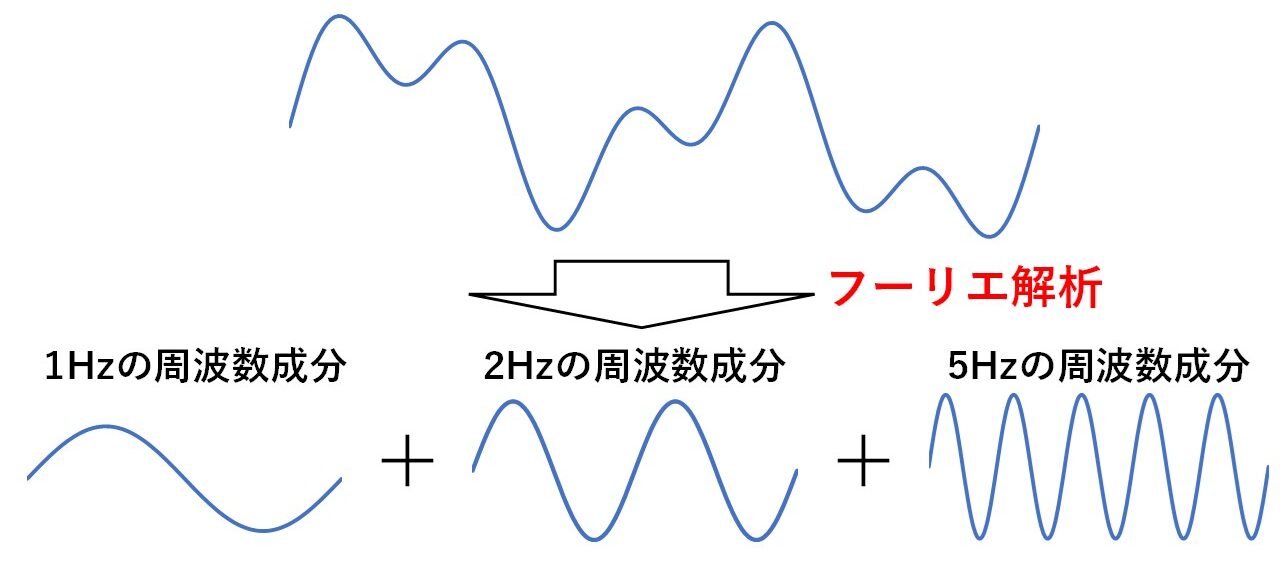
図1 フーリエ解析のイメージ
フーリエ解析の種類
図2のように，フーリエ解析では周波数を分析したい信号や波形が，①デジタル信号（値がとびとびの離散的な信号）なのかアナログ信号（値が連続的な信号）なのか，②周期性があるかないかによって，使用する手法が変わります！
例えば，この記事で説明するフーリエ変換は，アナログ非周期信号にどんな周波数が含まれるかを知りたい場合に使用する方法になります！アナログ周期信号に含まれる周波数成分が知りたい場合は，フーリエ級数展開を使います！
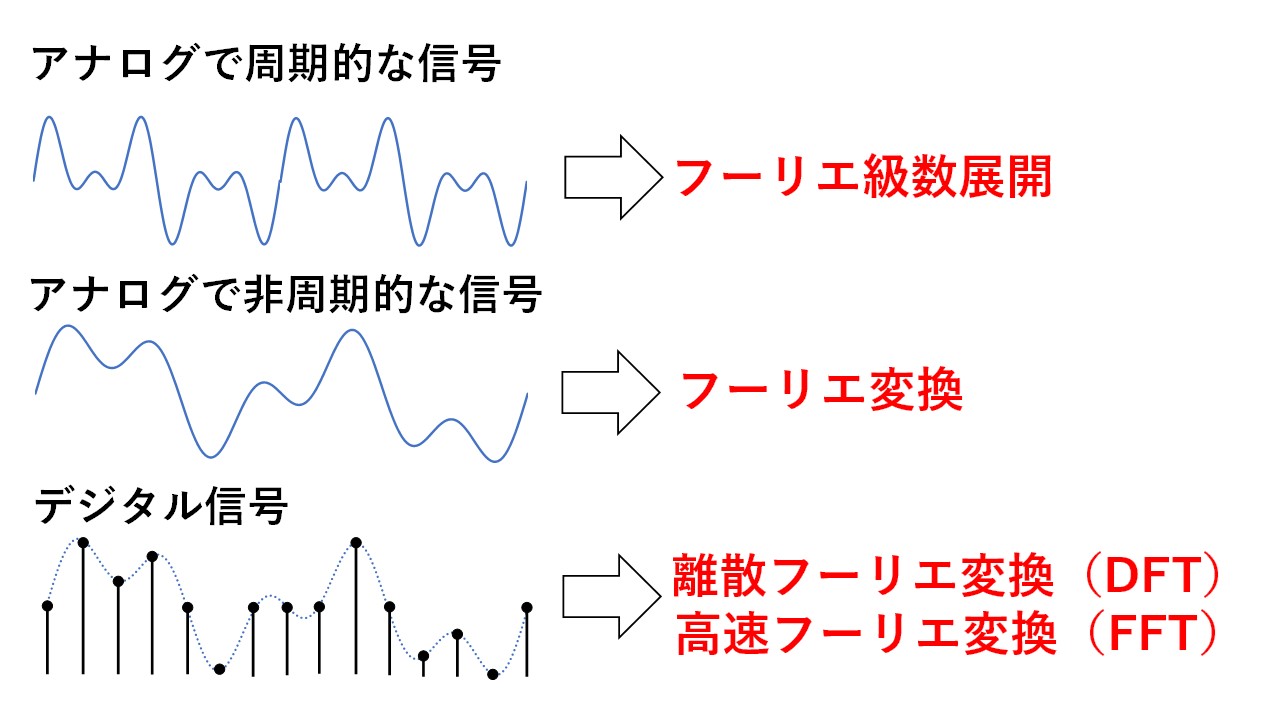図2 フーリエ解析の種類
フーリエ変換の概要
フーリエ変換とは，図3のように非周期的なアナログ信号（連続的な波形）にどんな周波数成分が，どんな大きさで含まれているかを知りたいときに使用する手法です！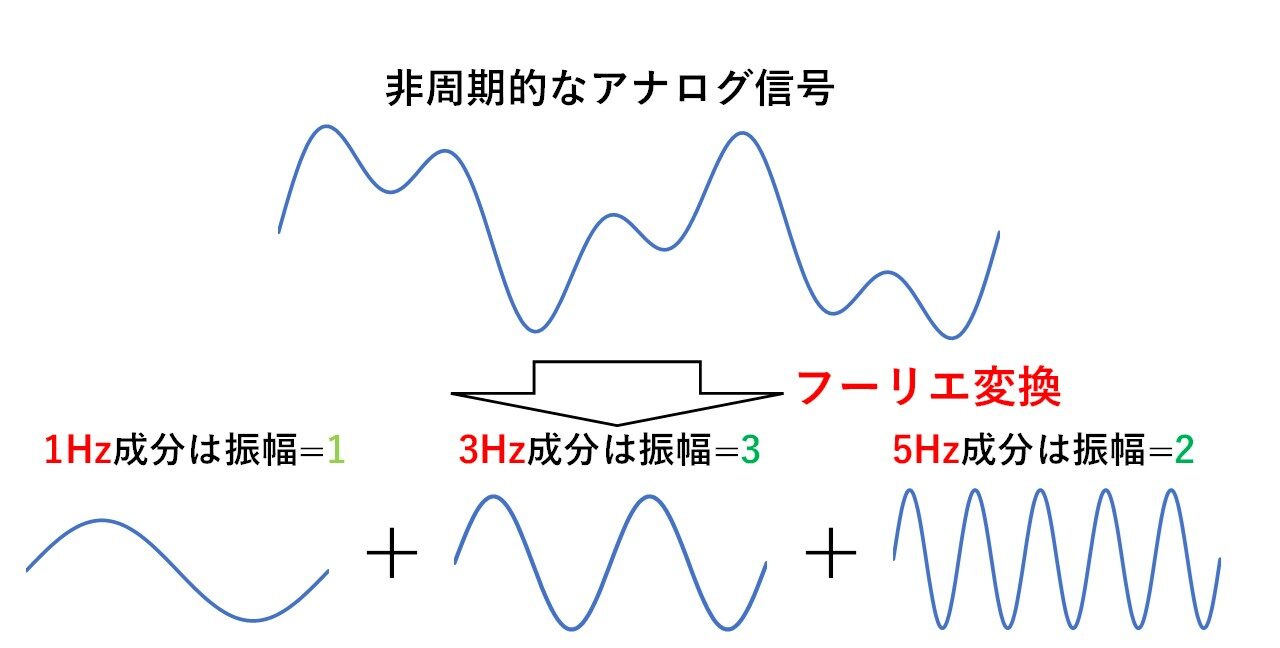
図3 フーリエ変換の概要
フーリエ変換とフーリエ級数展開の関係
この記事では，フーリエ変換でどのようにして非周期的なアナログ信号に含まれる周波数成分が分かるのかを，フーリエ級数展開をベースに説明します！なぜそうするかというと，それはフーリエ変換の基礎は全てフーリエ級数展開に詰まっていること，そしてこの2つは全く別のものではなく，単に扱う信号の周期が違うだけだからです！
フーリエ級数展開については，以下の記事で分かりやすく解説していますので是非参考にしてください(^^)/
ここではまずこの2つの関係性について説明します！フーリエ変換とフーリエ級数展開の関係性をまとめたのが図4になります！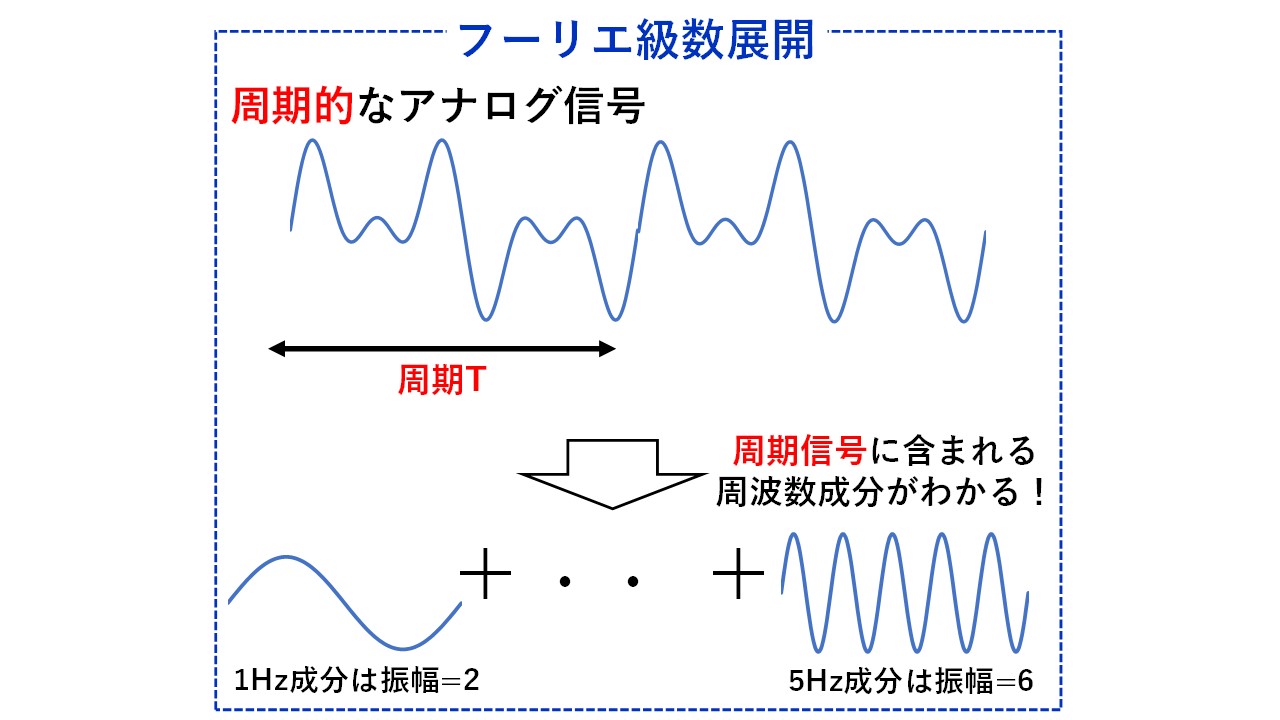 
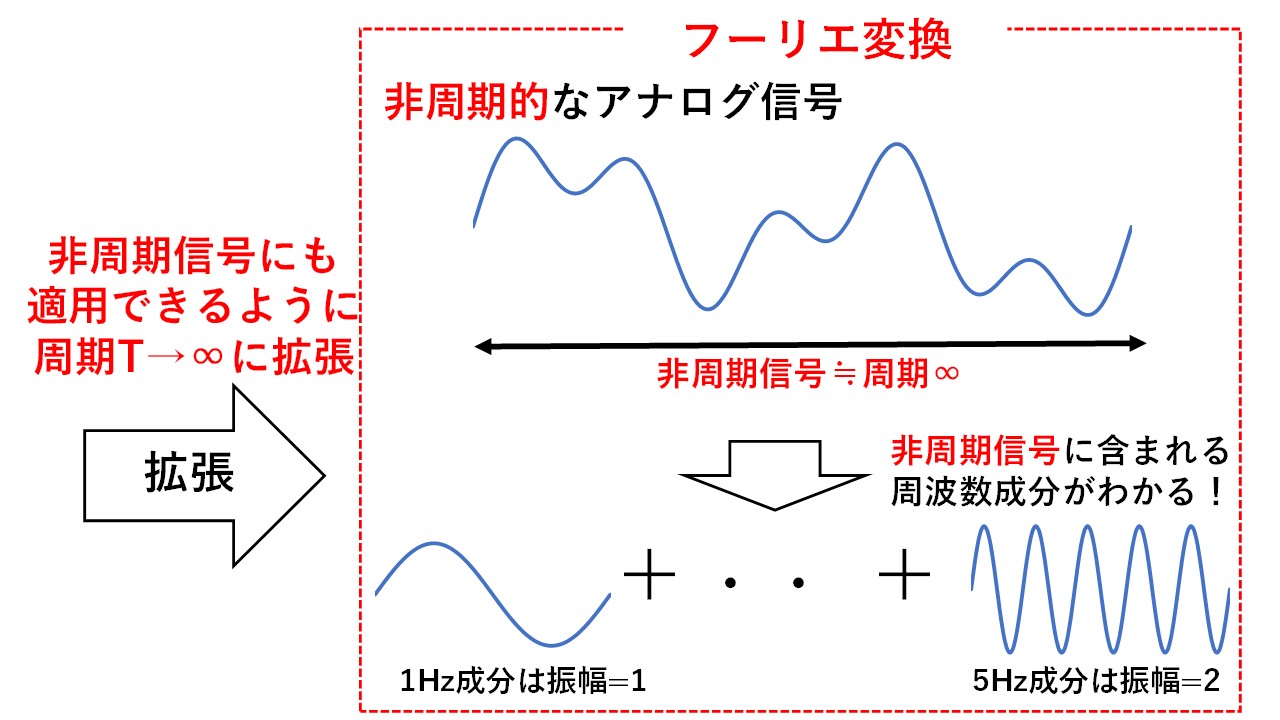図4 フーリエ変換とフーリエ級数展開の関係
実はフーリエ変換とは，フーリエ級数展開において周期Tを∞に考えたものになります！非周期的なアナログ信号に含まれる周波数成分を解析したい場合，フーリエ級数展開では周期的なアナログ信号に対してしか適用できないため，解析することができません！そこで，非周期的なアナログ信号に対しても適用できるように拡張したものがフーリエ変換になります！非周期信号は言い換えると周期∞の信号と考えることができるので，フーリエ級数展開において周期Tを∞に考えることで，非周期的なアナログ信号に含まれる周波数成分を解析することができます！
ここまでの話で，フーリエ変換の基礎はフーリエ級数展開にあることが分かって頂けたかと思います！本記事では，ある程度フーリエ級数展開を理解していることを前提として説明しますので，フーリエ級数展開の理解がまだの方は是非以下の記事（無料）を読んでみてください(^^)/
フーリエ変換とフーリエ級数展開の比較「数式編」
ここでは，フーリエ変換でどのようにして非周期的なアナログ信号に含まれる周波数成分が分かるのかを，フーリエ級数展開と対比しながら説明します！
図5に，フーリエ変換とフーリエ級数展開の式を示します！前述したようにフーリエ級数展開で周期Tを∞にしたのがフーリエ変換であるため，実際にフーリエ級数展開を複素数で表した複素フーリエ級数展開の式で周期Tを∞にすると，フーリエ変換の公式を導出することができます！こちらは証明が長いので，興味がある方は，記事の最後にある(参考)を是非見てみてください！
図5 フーリエ級数展開とフーリエ変換の比較（数式編）
図5から分かる重要な点は，以下の2つです！
①（フーリエ変換の時間関数の式より）非周期信号x(t)にどんな周波数成分がどんな大きさで含まれるかは，X(f)が求まれば全部分かる！
参考）フーリエ級数展開の場合
フーリエ係数amやbm等が求まれば，周期信号x(t)にどんな周波数成分が含まれるかが分かる！
②（フーリエ変換の周波数関数の式より）X(f)は周波数成分（exp-j2πft）をx(t)にかけて積分するだけで，簡単に求めることができる！
参考）フーリエ級数展開の場合
cos(2πmt/T)やsin(2πmt/T)を周期信号x(t)にかけて積分するだけで，フーリエ係数amやbmを簡単に求めることができる！
上記の①，②から，フーリエ変換もフーリエ級数展開と同様に，X(f)を簡単に求めることができ，それによって非周期信号に含まれる周波数成分を知ることができるというわけですね(^^)/
なお，時間関数x(t)について，フーリエ級数展開では色々な周波数成分をΣで足し合わせるのに対し，フーリエ変換では∫で足し合わせています！これは，フーリエ級数展開とフーリエ変換のスペクトルを見ると分かりやすいので，以下で説明します！
フーリエ変換とフーリエ級数展開の比較「スペクトル編」
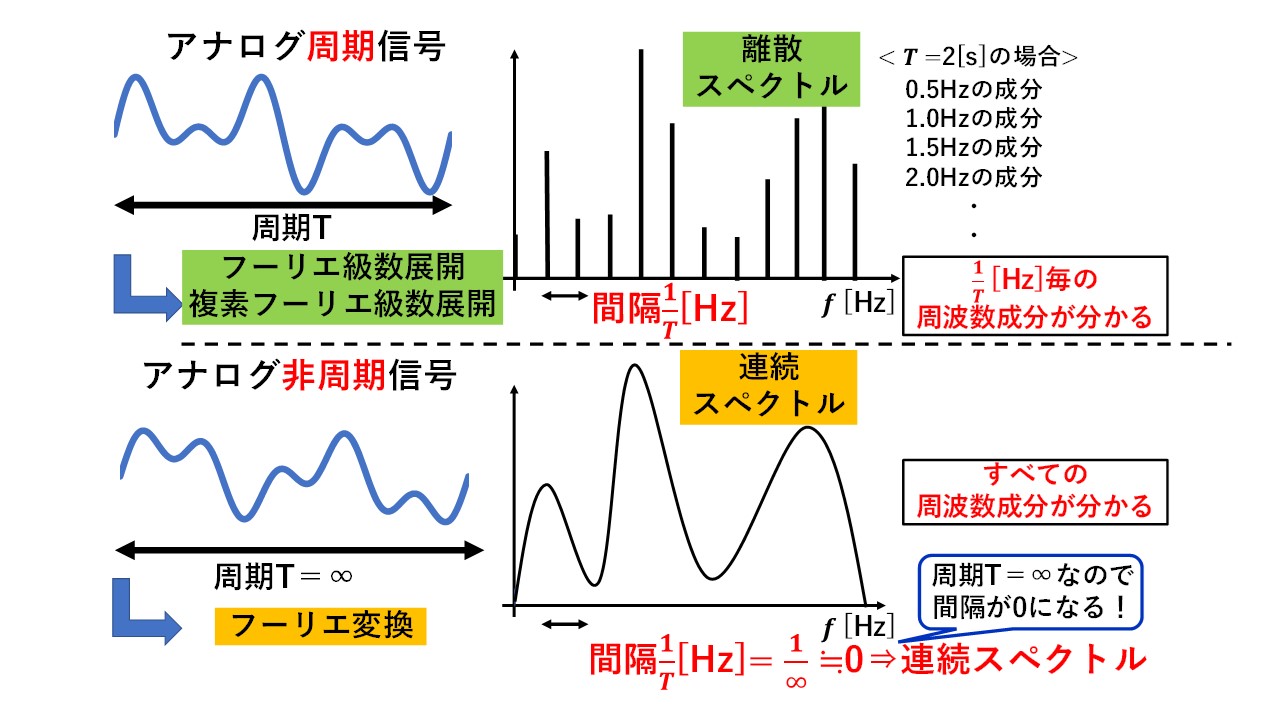
図6にフーリエ級数展開とフーリエ変換のスペクトルを示します！
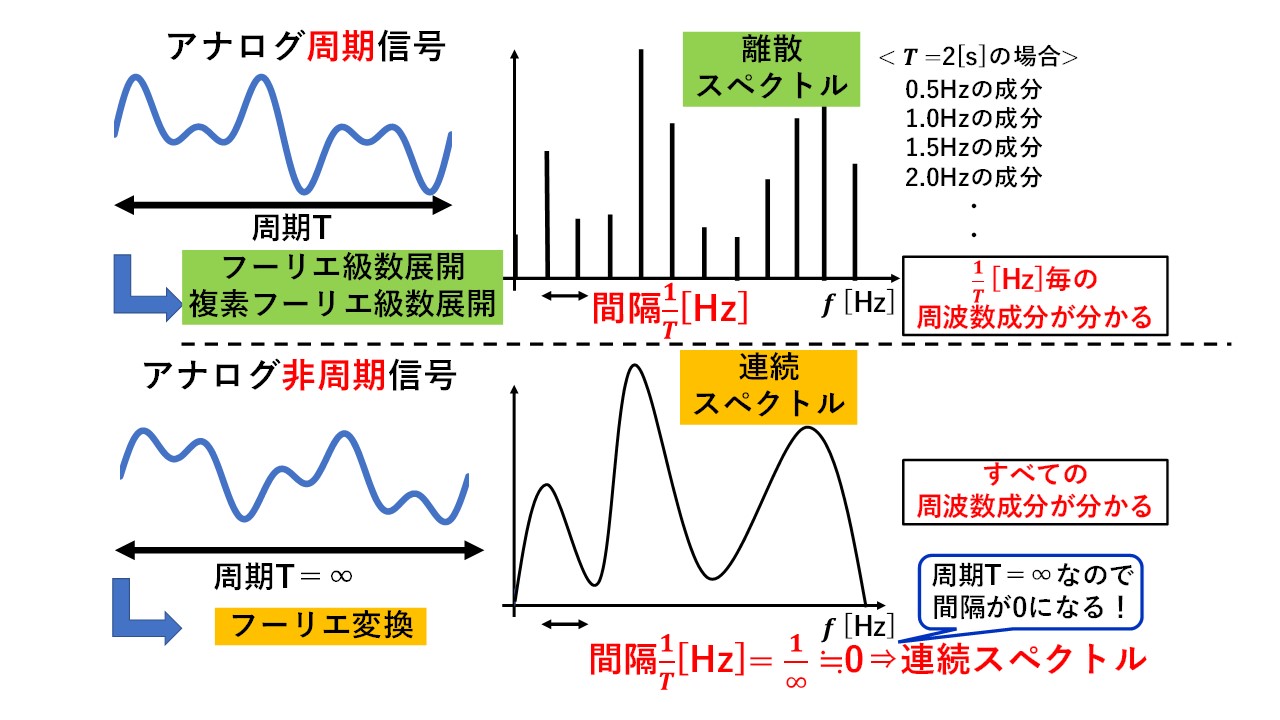図6 フーリエ級数展開とフーリエ変換の比較（スペクトル編）
フーリエ級数展開のスペクトルは，間隔が1/T[Hz]でとびとびの離散的なスペクトルであるのに対し，フーリエ変換のスペクトルは間隔のない連続的なスペクトルであることが分かります！フーリエ級数展開では周期Tの信号を考えているため，スペクトルの間隔は1/T[Hz]でとびとびですが，フーリエ変換では周期Tが∞の非周期信号を考えているため，スペクトルの間隔は1/T=1/999999999・・≒0となり，間隔が全くない連続スペクトルになります(^^)/
スペクトルの違いが分かった今，なぜ図5の時間関数x(t)で，フーリエ級数展開ではΣが登場し，フーリエ変換では∫が登場するかは，もう分かりますね？フーリエ級数展開でΣを使うのは周波数成分が離散量（とびとび）であるためで，フーリエ変換で∫を使うのは周波数成分が連続量であるためですね！
まとめ
・フーリエ変換とは，非周期的なアナログ信号にどんな周波数成分がどんな大きさで含まれているかを把握する手法である！
・非周期信号に含まれる周波数成分は，X(f)が求まればすべて分かる！そしてX(f)は周波数成分（exp-j2πft）をx(t)にかけて積分するだけで，簡単に求めることができる！
・上記の考え方は，フーリエ級数展開とほぼ同じである！これは，フーリエ級数展開とフーリエ変換では考える信号の周期が違うだけで，本質は同じためである！
（参考）フーリエ級数展開から複素フーリエ級数展開の導出
ここでは，フーリエ級数展開を単に複素数表現したのが複素フーリエ級数展開であることを証明するために，フーリエ級数展開の式から複素フーリエ級数展開の式を導出します！導出過程自体を覚える必要はありませんので，初学者の方は読み飛ばしても問題ございません！
フーリエ級数展開の式のsinやcosをオイラーの公式によりexpを使って表すと，以下の式が得られます！
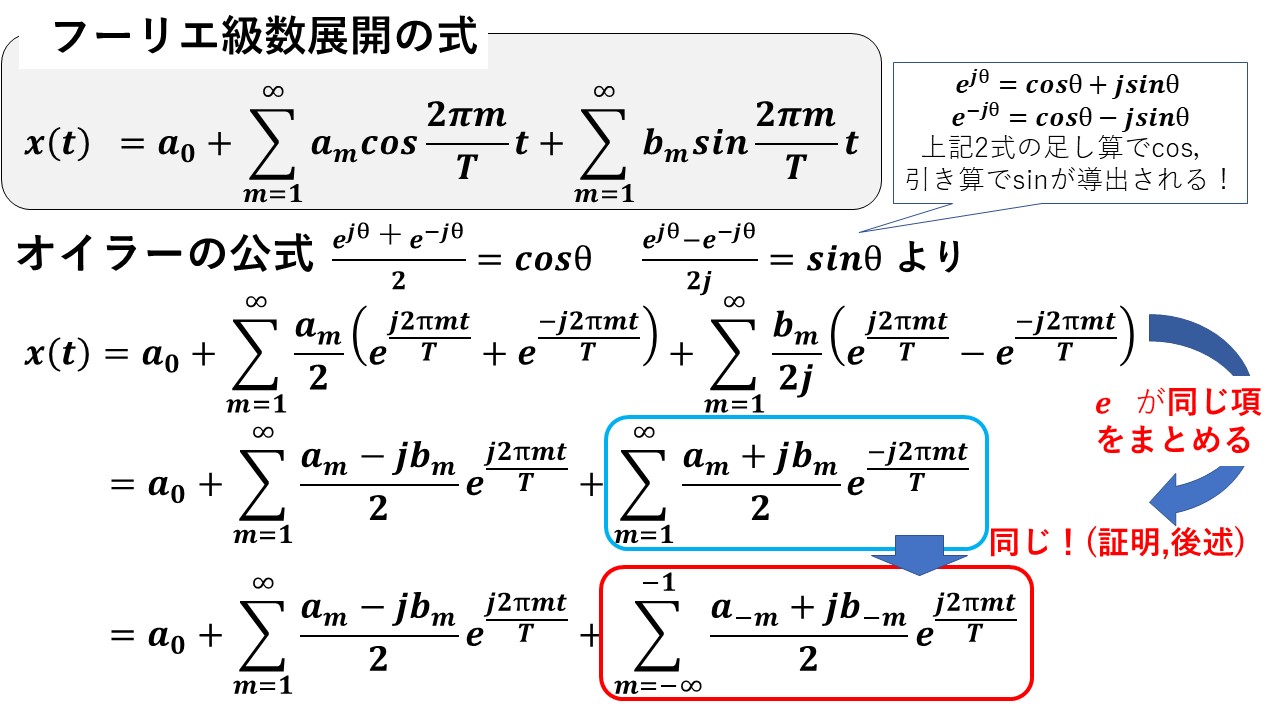
ここで，上記の式で青枠で囲んだ項から赤枠で囲んだ項への変形は，以下を根拠に行っています！見た目は変わっていますが，要するに足す順番が変わっただけというのが分かると思います！
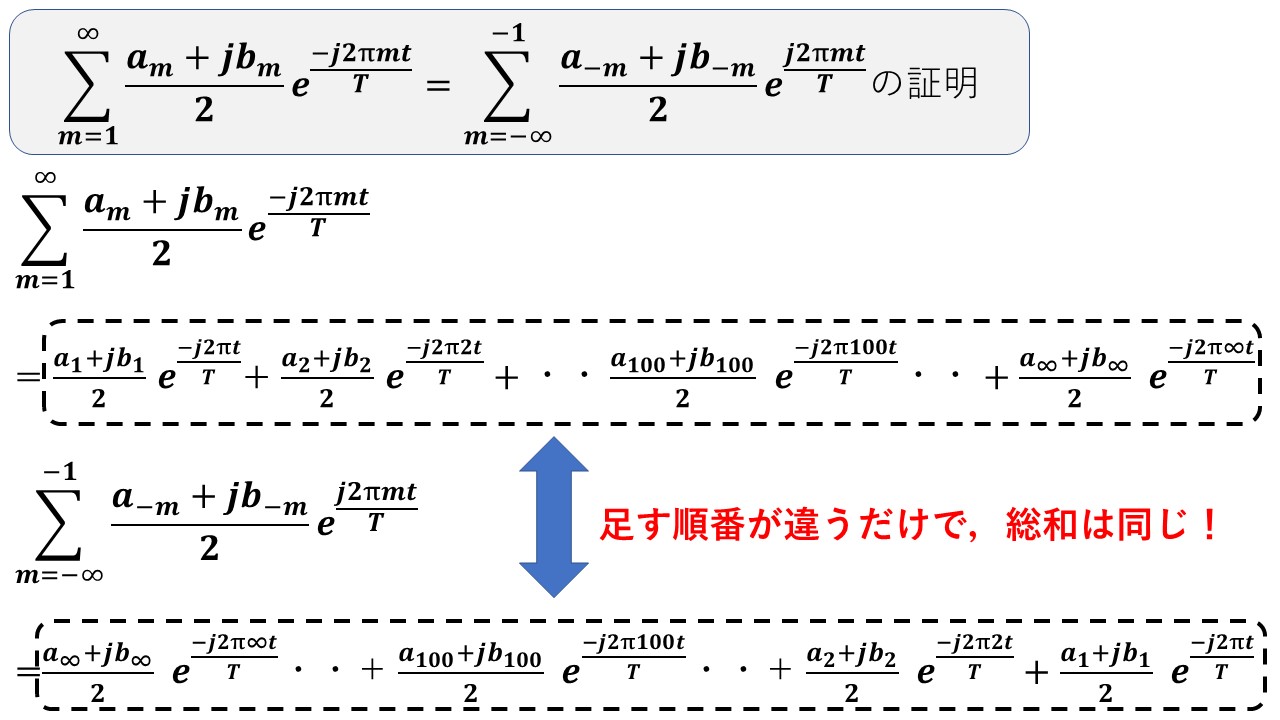
続いて以下の赤枠の項を，黄色の項へ変形します！これは，exp(j2πmt/T)の係数を(am-jbm)/2に統一することで，a0以外の2つのΣの項を後々1つにまとめるためです！
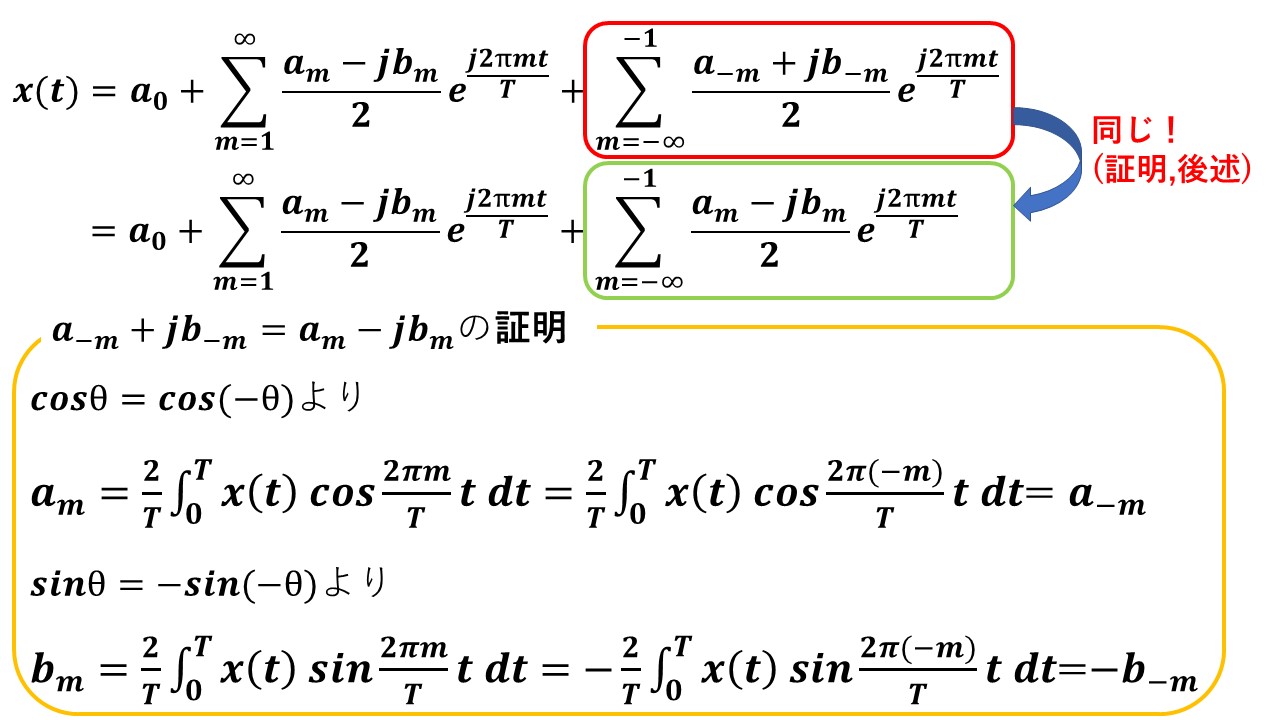
exp(j2πmt/T)の係数が(am-jbm)/2に揃ったので，これをXmと定義することで，m=0以外の項については1つの項にまとめることができます！また，X0=a0と定義することで，m=0も含めて1つの式で表すことができます！
この式は，図5の複素フーリエ級数展開の式になっていますね！
以上から，フーリエ級数展開の式から複素フーリエ級数展開の式を導出することができました(^^)/
（参考）複素フーリエ級数展開からフーリエ変換の導出
ここでは，複素フーリエ級数展開の式からフーリエ変換の式を導出します！証明自体は長いので，初学者の方は読み飛ばしても問題ございません！
まず重要な点なので繰り返しになりますが，フーリエ変換はフーリエ級数展開において周期Tを∞にして考えたものです！これは以下の導出過程でも使いますので，覚えておきましょう(^^)/
複素フーリエ級数展開の式に複素フーリエ係数Xmの式を代入し，fmやΔfを以下のように定義すると，複素フーリエ級数展開の式は以下のように変形できます(^^)/
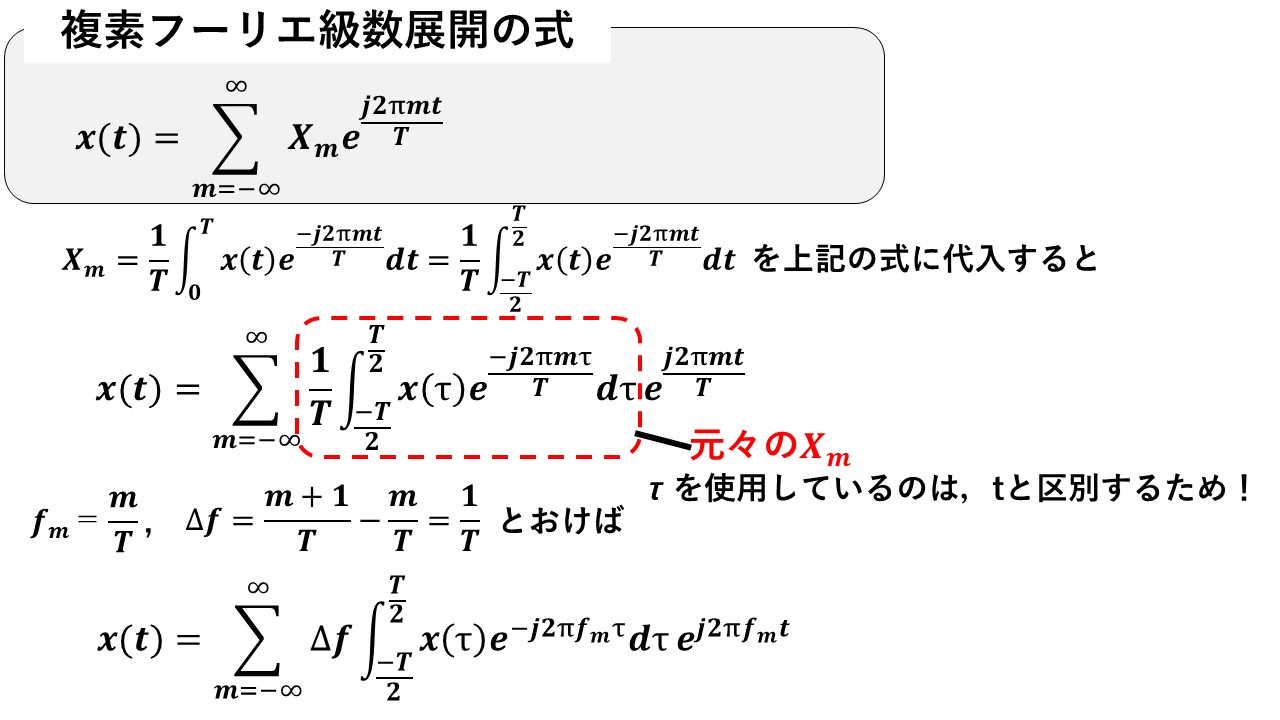
ここで，以下の赤枠で囲んだ項をX'(fm)と定義すると，x(t)は下図のように青枠で囲んだ長方形を沢山足し合わせていった面積の総和に等しいということが分かります！
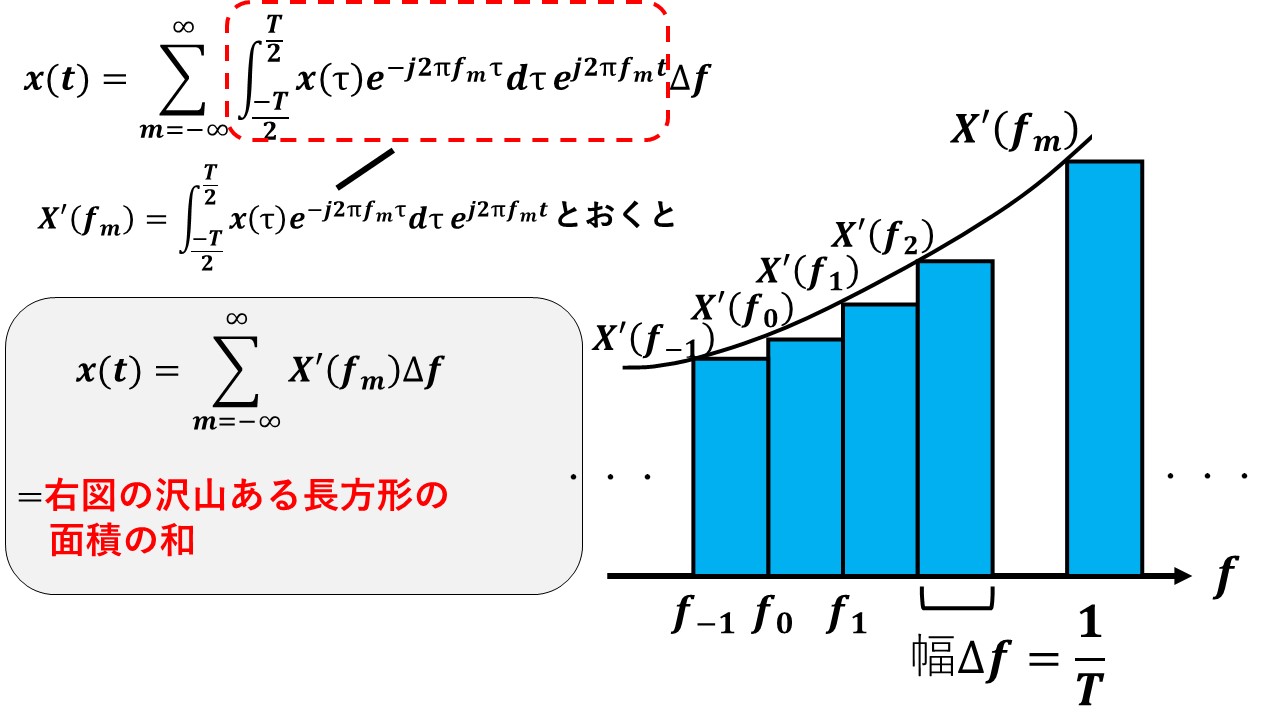
ここで，ようやく周期T→∞を考えます！
T→∞とすると，Δf=1/T≒1/99999999・・≒0となるため，限りなく長方形の横幅が0に近くなり，隙間だらけだった以下の左図の長方形の面積の総和は，右図のようにX'(f)の関数をf=－∞～∞まで積分した面積に限りなく近くなります！まさに，高校数学で習った区分求積法の発想です！（※）
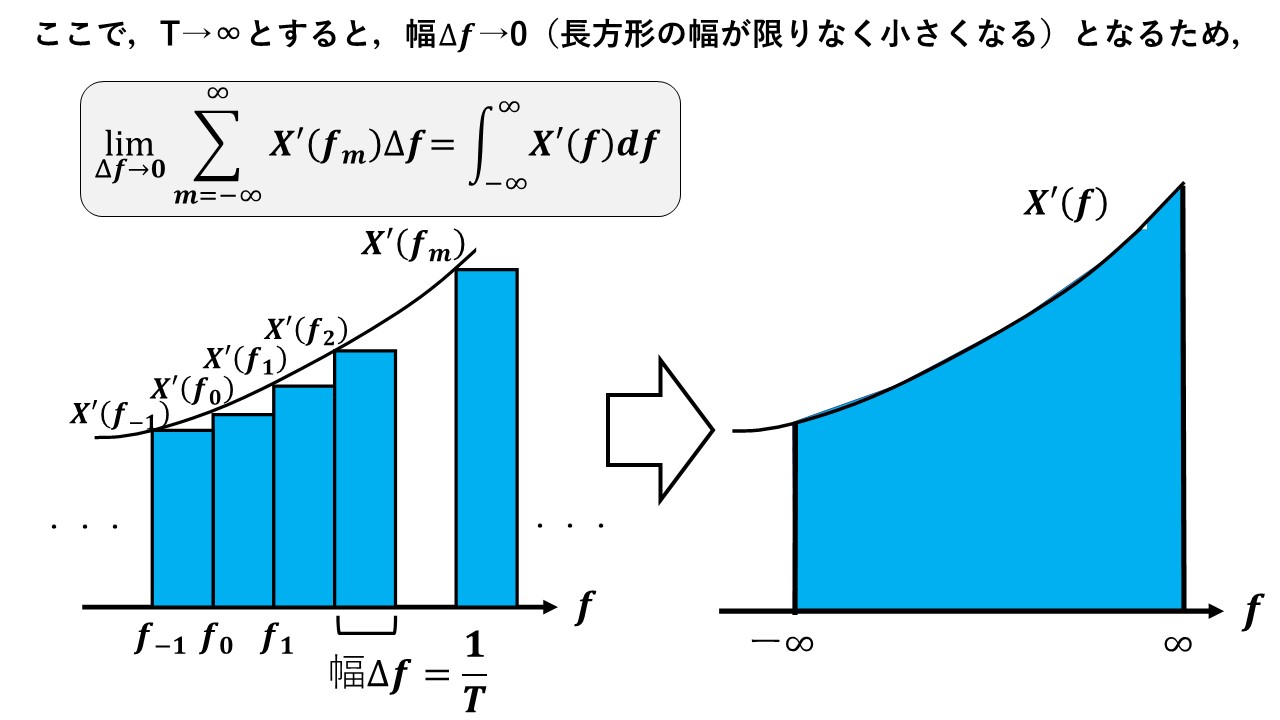
結果として，T→∞を考えると，Σ⇒∫，fm（離散的）⇒f（連続的），Δf（離散的）⇒df（連続的）になるので，X'(fm)はX'(f)に変形され，x(t)は以下の式に変形されます！
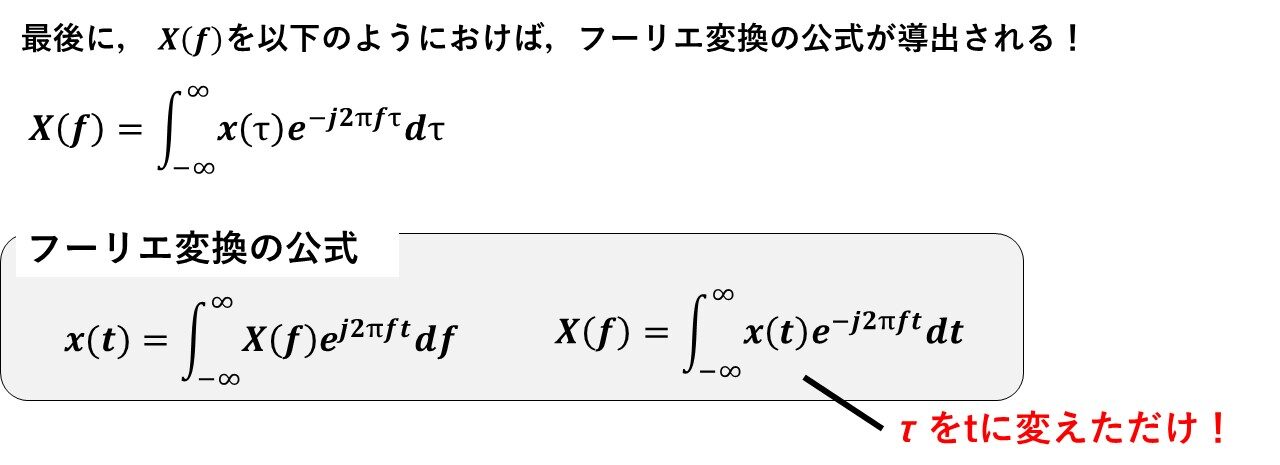
最後に，X(f)を新しく以下のように定義すれば，フーリエ変換の公式が導出されます！
（※）細かい話ですが，区分求積法について説明した際，何も断らずに-∞～∞までの積分を考えましたが，実はこの積分を考えるためには条件がつきます！それが以下の条件です！特に②の絶対可積分の条件には注意しましょう(^^)/
今回の記事は以上です。この記事が，皆さんの役に少しでも立っていれば幸いです(^^)/
