こんにちは，ハヤシライスBLOGです！今回は周波数伝達関数についてできるだけ分かりやすく解説します。
周波数伝達関数とは
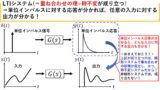
周波数伝達関数G(jω)とは，ある線形なシステムに正弦波を入力した場合の伝達特性を表現するものです(^^)/ 要するに，線形システムであれば，正弦波を入力したときに，出力波形がどうなるかを周波数伝達関数によって把握できるということです！
ちなみに，任意の入力波形に対する伝達特性は，周波数伝達関数G(jω)ではなく，伝達関数G(s)が必要となりますのでご注意を(^^)/
周波数伝達関数のメリット
周波数伝達関数を用いるメリットは，大きく以下の3つがあります！この記事では，メリット1のゲイン特性・位相特性を中心に解説します(^^)/
メリット1：ゲイン特性・位相特性
⇒ゲイン特性・位相特性によって，線形システムに入力した正弦波が，出力される時に大きさ・位相がどう変化するかを把握できる
図1 ゲイン特性・位相特性
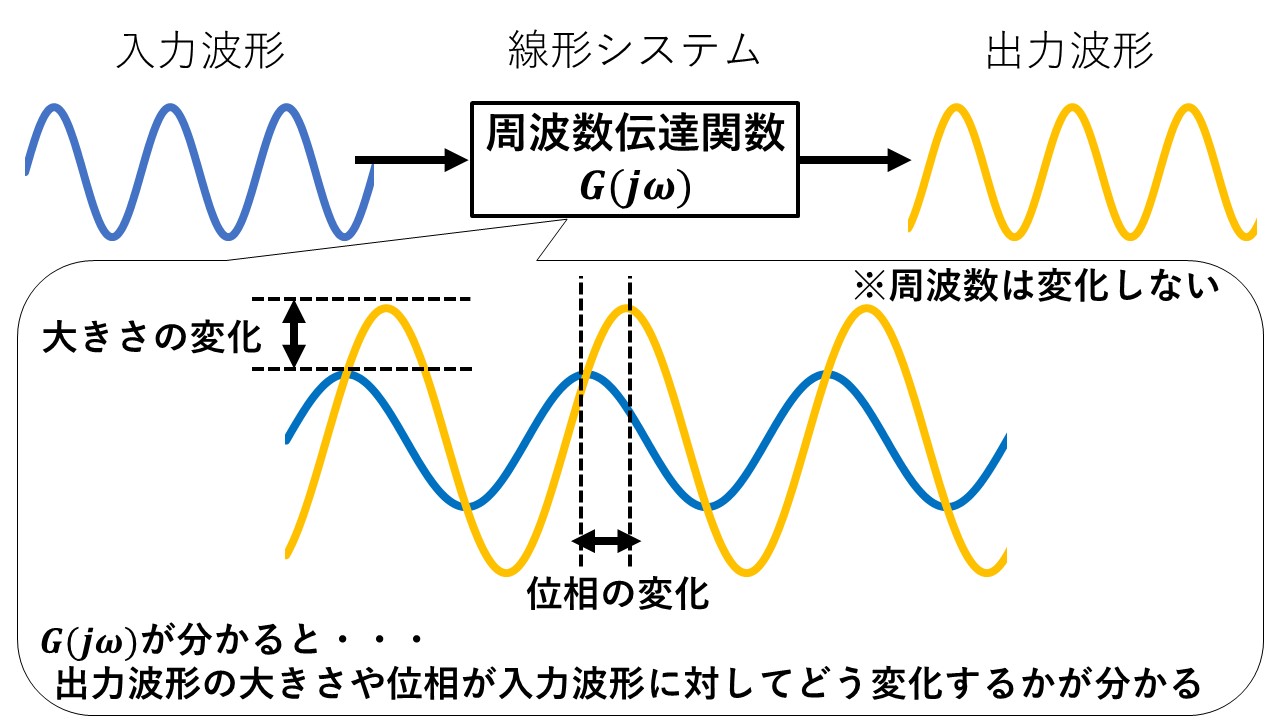
メリット2：フィードバック制御系の安定・不安定を判別
⇒開ループ伝達関数G(jω)H(jω)によって，フィードバック制御系の安定・不安定を判別できる
図2 フィードバック制御系の安定判別
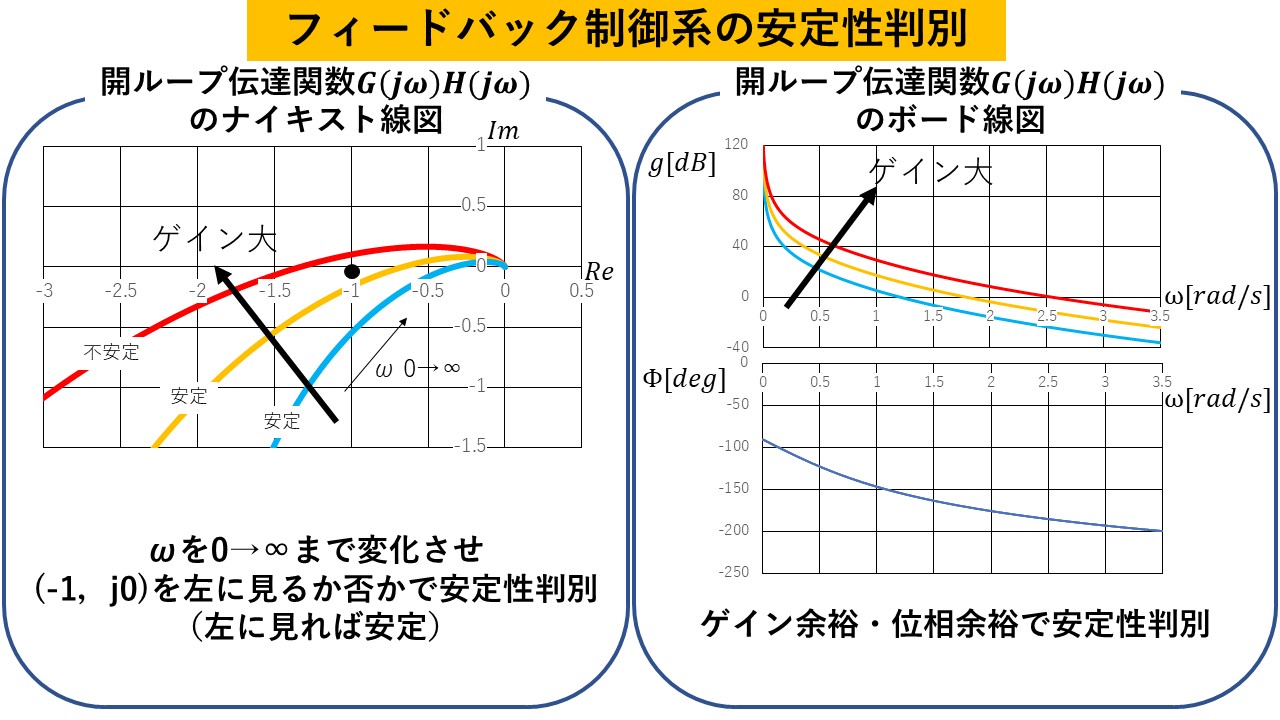
メリット3：時間領域から周波数領域
⇒時間領域で線形システムの出力を得るには複雑な畳み込み積分を必要としたが，周波数領域で考えることで単なるかけ計算により出力を計算できる
図3 周波数領域での計算
メリット1：ゲイン特性，位相特性
周波数伝達関数が分かると，ある線形なシステムに正弦波を入力したときに，そのシステムから出力される正弦波の大きさや位相が入力波形からどう変化するかを即座に把握することができます！
RL回路の例
ゲイン特性・位相特性によって，出力波形の大きさ・位相が入力した正弦波に対してどう変化するかが分かる，というのを図4のRL回路を例に説明していきます！
この電圧を入力，電流を出力とした線形システムの周波数伝達関数，ゲイン，位相は，図4右下の数式で表すことができます！
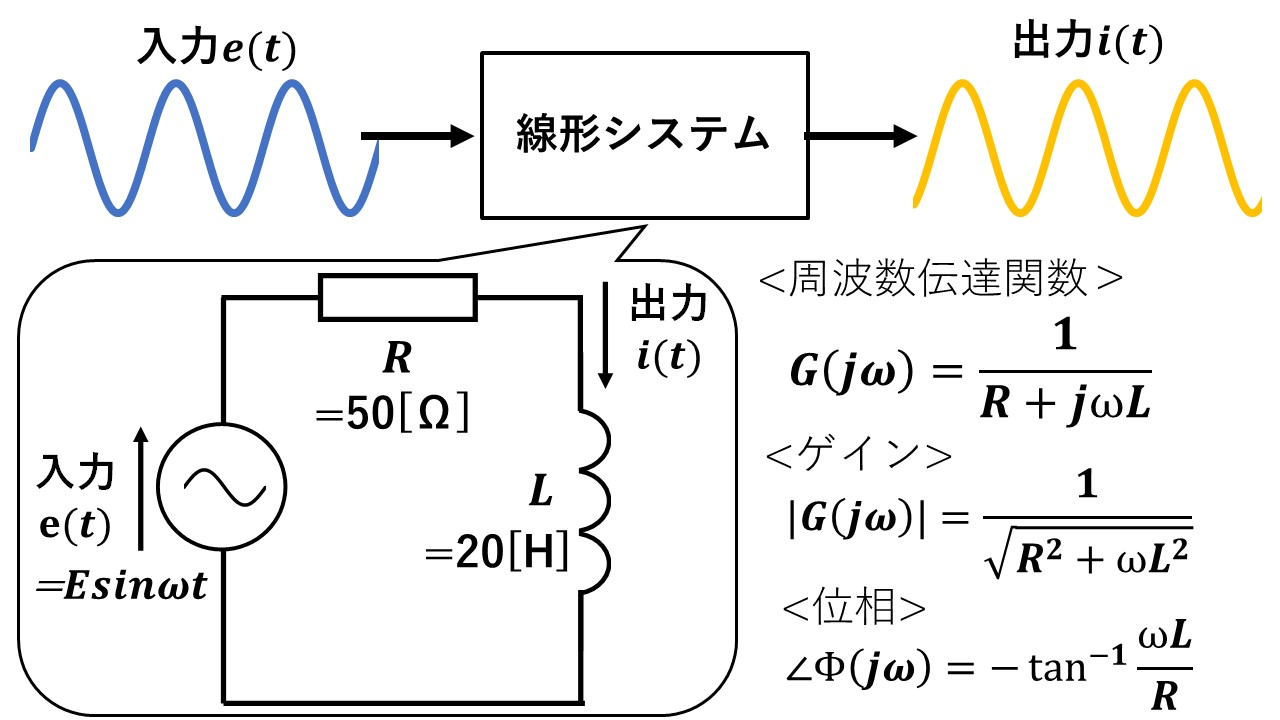
図4 例題 RL回路
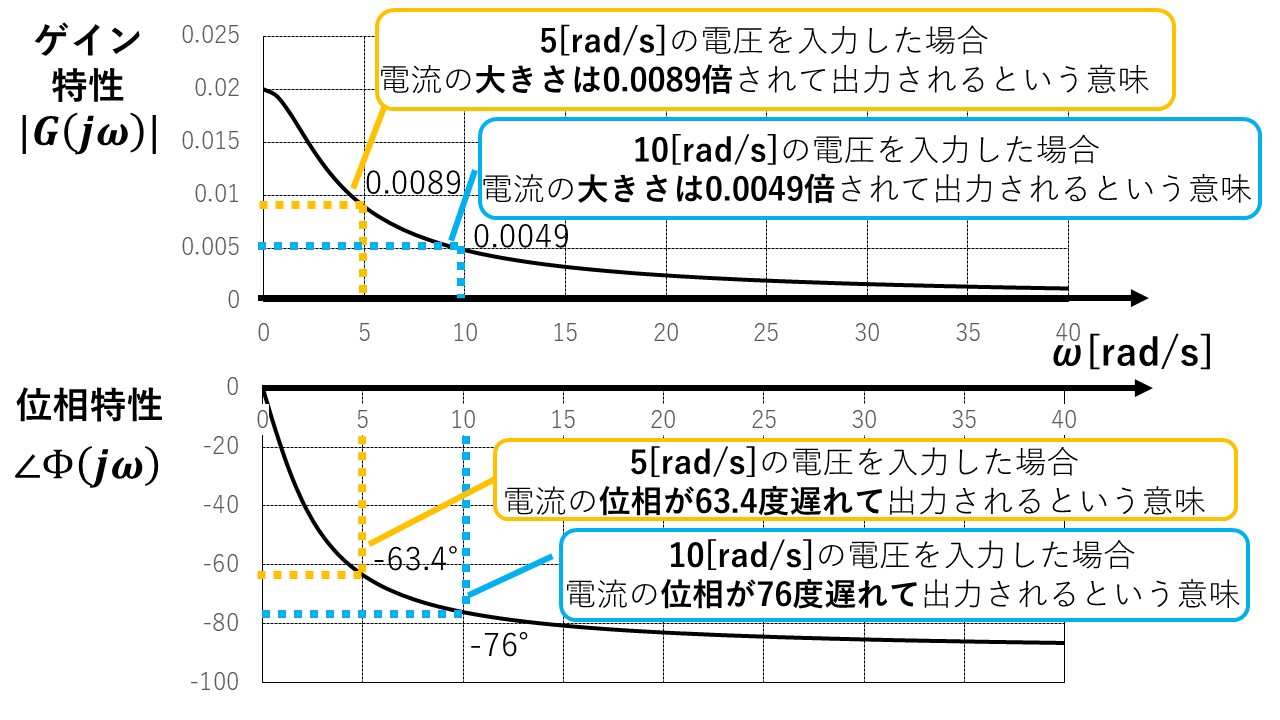
R=50[Ω]，L=20[H]を代入し，ゲイン特性および位相特性を図示すると，図5になります。この図は，入力波形に対して出力波形の大きさや位相がどう変化するのかを，入力される正弦波の周波数ごとに示しています！ 下の2つの例を見てみましょう(^^)/
図5 RL回路のゲイン特性・位相特性
例えば，
①ω=5[rad/s]の正弦波電圧を入力した場合は，
ゲイン|G|=0.0089，位相∠Φ=-63.4[deg]なので，出力電流は入力電圧に対して大きさが0.0089倍され，位相が63.4[deg]( =1.11[rad])遅れます！
つまり，e(t)=100*sin(5t)の波形を入力すれば，i(t)=100*0.0089*sin(5t-1.11)の波形が出力されます(^^)/
②ω=10[rad/s]の正弦波電圧を入力した場合は，
ゲイン|G|=0.0049，位相∠Φ=-76[deg]なので，出力電流は入力電圧に対して大きさが0.0049倍され，位相が76.0[deg](=1.33[red])遅れます！
つまり，e(t)=100*sin(10t)の波形を入力すれば，100*0.0049*sin(10t-1.33)の波形が出力されます(^^)/
このように，ゲイン特性・位相特性が分かると，単に入力波形の周波数が分かりさえすれば，複雑な計算をすることなく，出力波形が入力波形に対してどう変化するかを簡単に把握することができます！
（ちょっと休憩）理系大学生が学生時代に必ずやっておくべき5つのこと！！
大学生の皆さん！勉強お疲れ様です(>_<) 以下の記事は，私が理系の大学生の皆さんに向けて，社会人になる前にやっておいた方がよいことを5つに厳選して書いた記事です！これらは，私が社会人になって，「学生時代にこれをやっておいて本当に良かった！」と心から思うことや，「学生時代に何でこれをやっておかなかったんだろうか・・・」と超絶後悔していることなどを厳選しています(^^)/勉強の休憩がてらに，是非見てみてください！
解析解による検証
最後に，本当に周波数伝達関数から出力波形を把握できるのかを，解析解と比べて検証してみます！
図4のRL回路の電流の解析解は，微分方程式を真面目に解くと以下のように求めることができます！
図6 RL回路の解析解
このうち出力である電流の定常解と，入力である電圧の数式を比較すると，
電流の大きさは入力に対して1/√（R^2+(ωL)^2)倍され，位相はtan-1((ωL)/R)だけ遅れており，
図4の右下に示したゲイン|G(jω)|，位相の数式と結果が一致していることが分かります(^^)/
当然，ω=5[rad/s],10[rad/s]の時のゲイン，位相も，図5の中で説明した2つの例と同じ結果になります。
したがって，線形システムへ正弦波を入力した場合の出力(=定常解)が知りたければ，わざわざ解析解を求めなくても，周波数伝達関数によって出力を把握することができますね(^^)/
以上です。今回の記事では，周波数伝達関数のゲイン特性・位相特性を中心に解説しました！
この記事が，少しでも皆さんの役に立っていれば嬉しいです(^^)/
（参考）制御工学について分かりやすく解説！！
以下の記事では，制御工学に必要な基礎知識について，できるだけ分かりやすく解説しています！どれも無料で読めるので，是非見てみてください(^^)/
