こんにちは，ハヤシライスBLOGです！今回は制御工学のメインテーマであるナイキストの安定判別法について分かりやすく解説します(^^)/
ナイキストの安定判別法とは
ナイキストの安定判別法とは，フィードバック制御系の安定性を判別する方法の一つです！
特徴としては，フィードバック制御系全体の伝達関数ではなく，開ループ伝達関数G(s)H(s)の特性だけからフィードバック制御系全体の安定性を判別できることです！全体の伝達関数G(s)H(s)/(1+G(s)H(s))をわざわざ求めなくていいのは，嬉しいですね(^^)/
もう一つの特徴としては，システムが単に安定かどうかが分かるだけでなく，どの程度安定であるかまで分かることです！システムが仮に安定であっても，ギリギリ安定の場合は制御パラメータが少し変わるだけで不安定になってしまう可能性があるので安心できないですよね？ナイキストの安定判別法はどの程度安定かまで分かるので安心です！
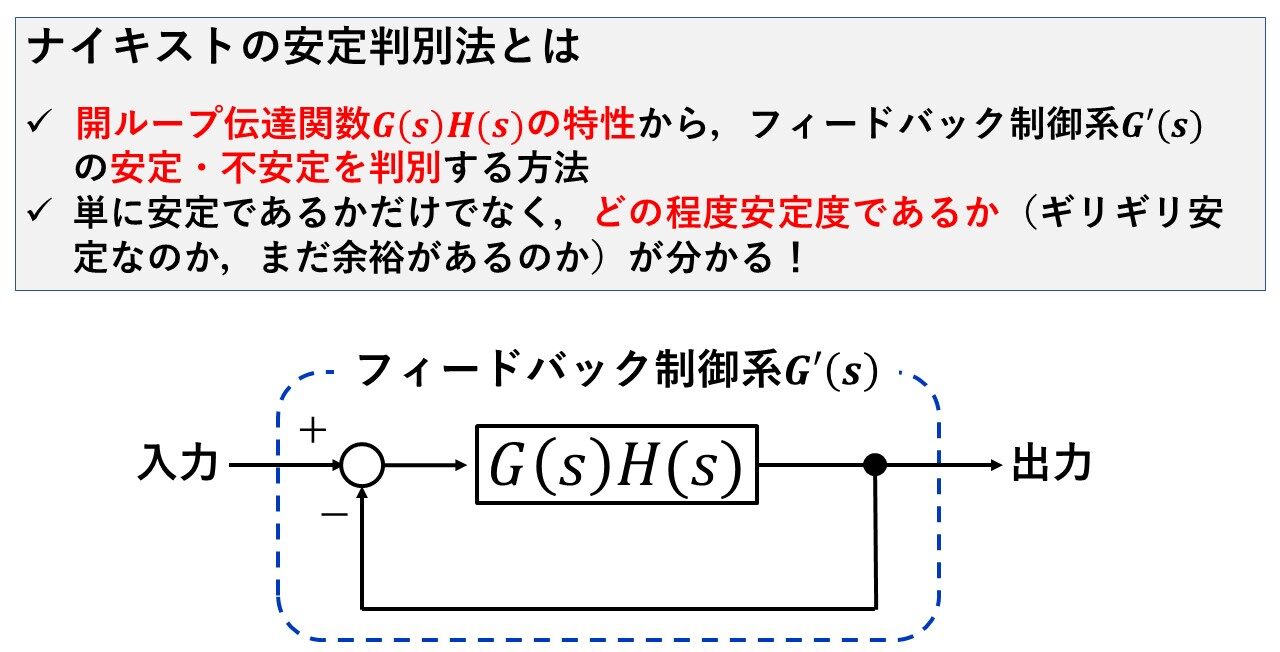図1 ナイキストの安定判別法の概要
① フィードバック制御系の安定性を判別できる！
それでは早速，以下のフィードバック制御系を例に，ナイキストの安定判別法でどのように安定性を判別できるか説明します(^^)/
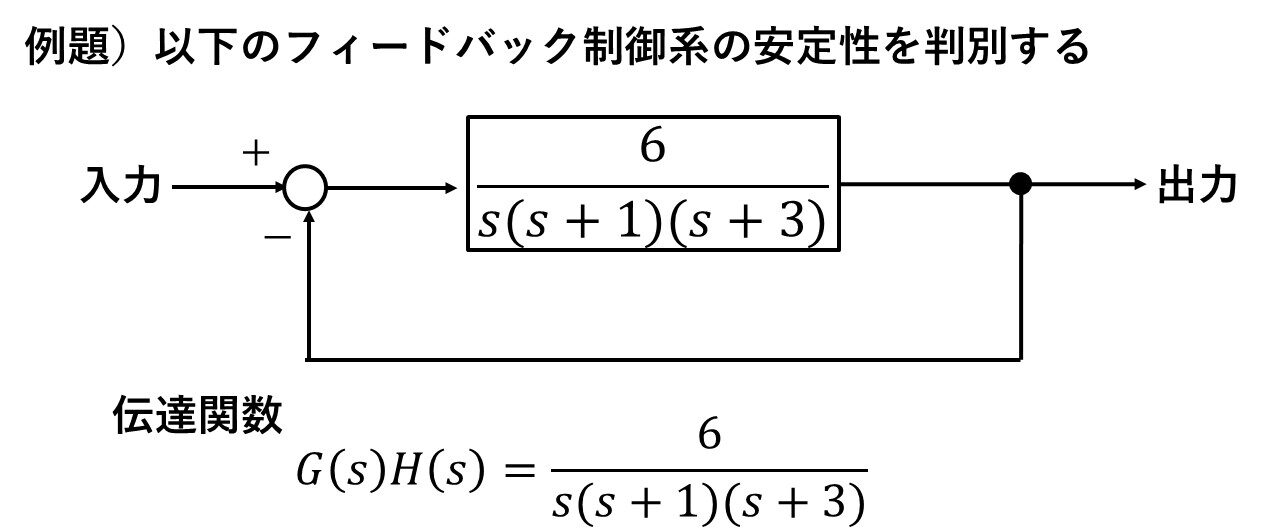図2 フィードバック制御系の例
周波数伝達関数を求めよう！
まずナイキストの安定判別法では，sの関数である伝達関数ではなく，jωの関数である周波数伝達関数を使いますので，sにjωを代入して，周波数伝達関数を求めましょう！
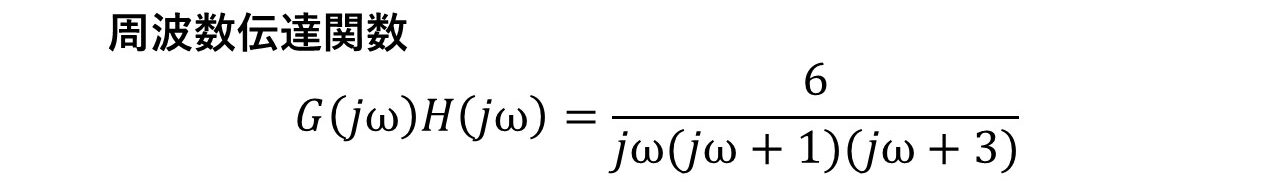
周波数伝達関数の実部と虚部を求めよう！
ナイキストの安定判別法では，周波数伝達関数の実部を横軸，虚部を縦軸としたナイキスト線図を使います！そのため，周波数伝達関数G(jω)H(jω)の実部と虚部を求めましょう！以下の方法では，まず周波数伝達関数の大きさと位相を計算し，その後に，Ae(jθ)=Acosθ+jAsinθの数式を利用して，実部と虚部を求めていますが，別にこのやり方でなくても，直接G(jω)H(jω)を○＋ｊ△の形に変形して実部と虚部を求めても構いません(^^)/
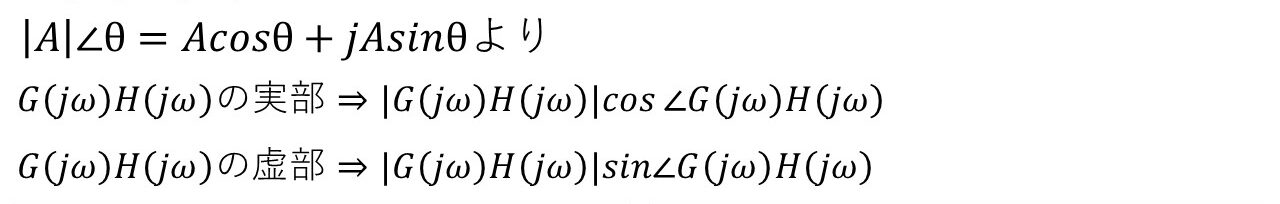図3 周波数伝達関数の実部と虚部の計算
ナイキスト線図を描いて，システムの安定・不安定を判別しよう！
上記で求めた周波数伝達関数G(jω)H(jω)の実部を横軸に，虚部を縦軸にしたナイキストを描きましょう！このナイキスト線図を描けば，もう安定性は判別できます！図4の通り，ωを0から∞にどんどん大きくしていった時の軌跡から見て，（-1、j0）の点を左側に見れば，そのフィードバック制御系は安定であると判断できます！
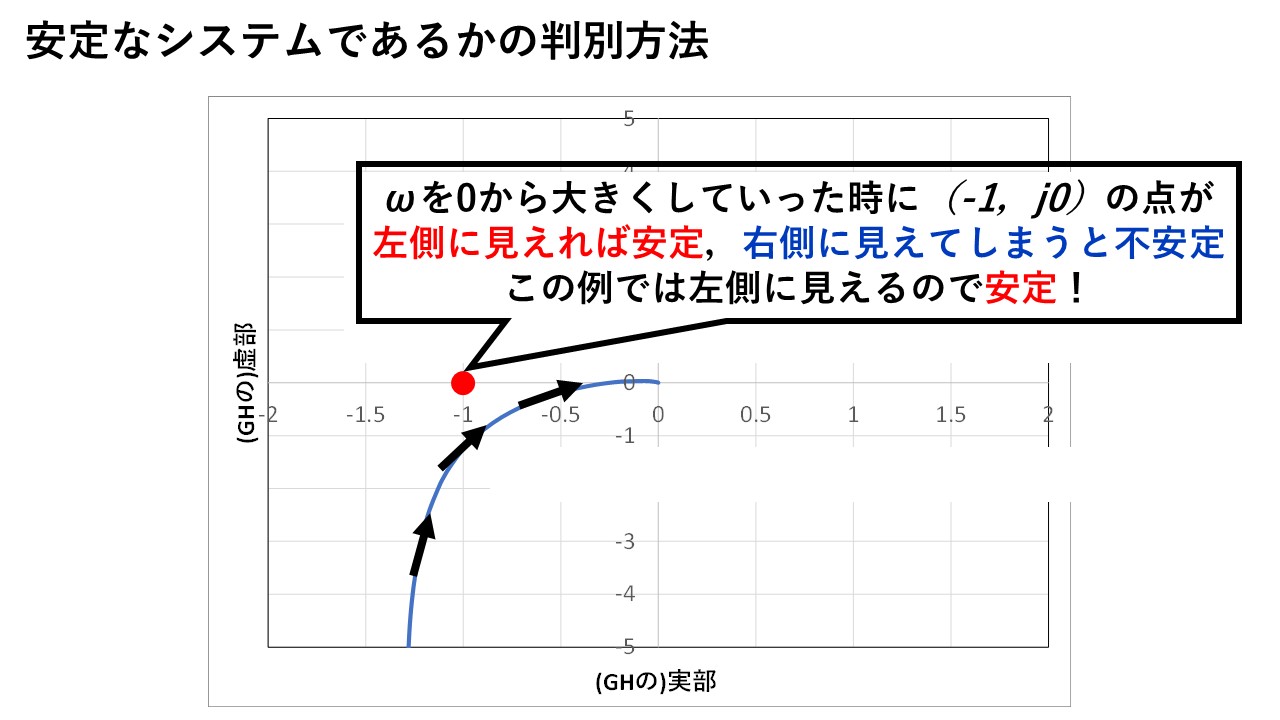図4 ナイキスト線図から安定性を判別しよう！
システムが安定の場合と不安定の場合のナイキスト線図の違い
念のため，フィードバック制御系が不安定である場合のナイキスト線図も見ておきましょう！
図5の左図は，これまでの例と同じG(jω)H(jω)のゲインが6の場合のナイキスト線図ですが，右図はそのゲインを3倍の18にした場合の図になります！この場合，ωを0から∞にどんどん大きくしていった時の軌跡から見て，（-1、j0）の点を右側に見えてしまうことが分かります！したがって，右側のフィードバック制御系は不安定と判断できます！
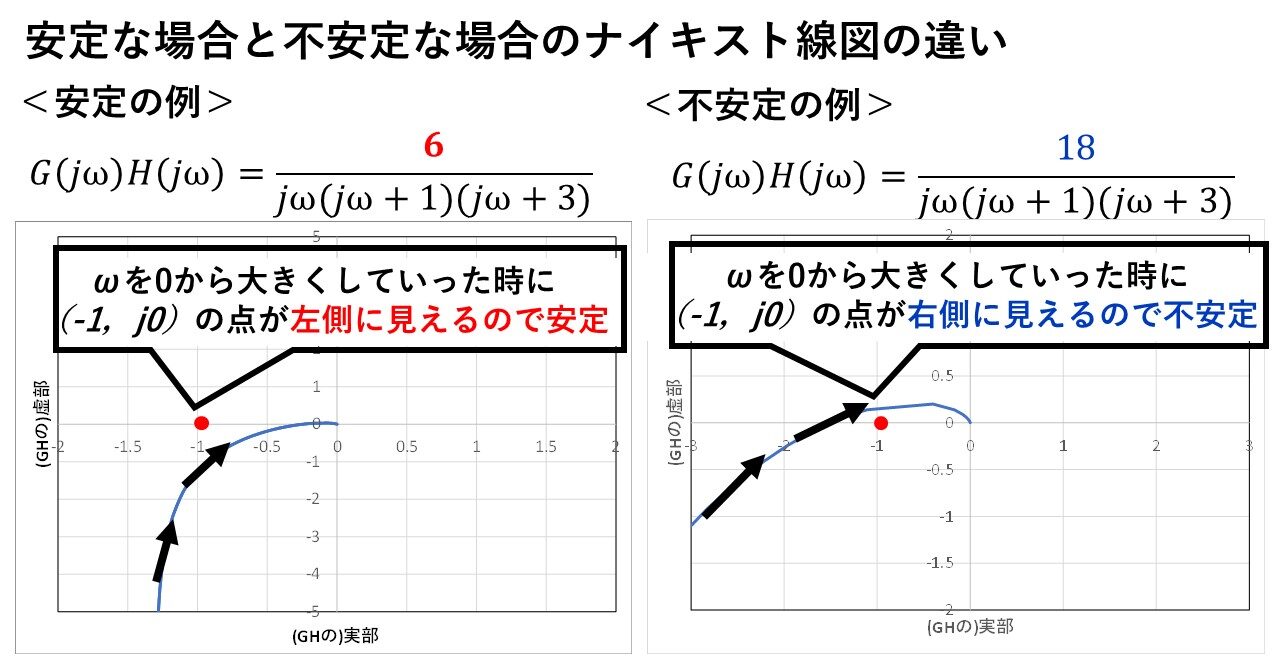図5 安定なシステムと不安定なシステムのナイキスト線図の違い
（参考）システム制御について分かりやすく解説
以下の記事では，システム制御のテーマについて，分かりやすく解説しています！是非参考にしてみてください(^^)/
② フィードバック制御系がどの程度安定であるかを把握できる
ここまでの説明で，ナイキストの安定判別法からフィードバック制御系の安定性を判別できることが分かりました！次は，フィードバック制御系がどの程度安定かを把握する方法を説明します！やり方は簡単で，（-1、ｊ0）の点を余裕をもって左側に見れれば余裕で安定，ギリギリ左側に見る場合はギリギリ安定です！
図6はG(jω)H(jω)のゲインをそれぞれ3，6，18にした場合のナイキスト線図になります！ゲインが3の場合も6の場合も，（-1,j0）の点を左側に見るので安定ですが，ゲインが3の場合の方が(-1,j0)の点から距離が離れているので，余裕で安定であることが分かります！
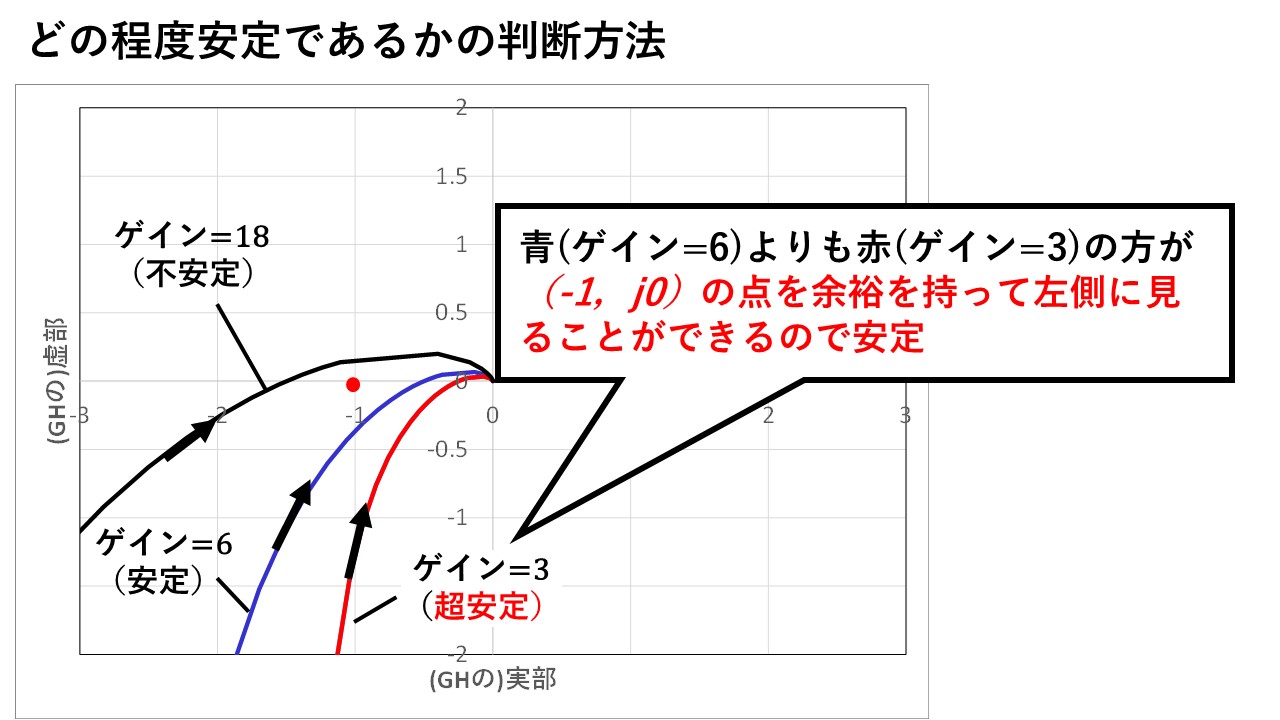図6 システムがどの程度安定であるかを把握する方法
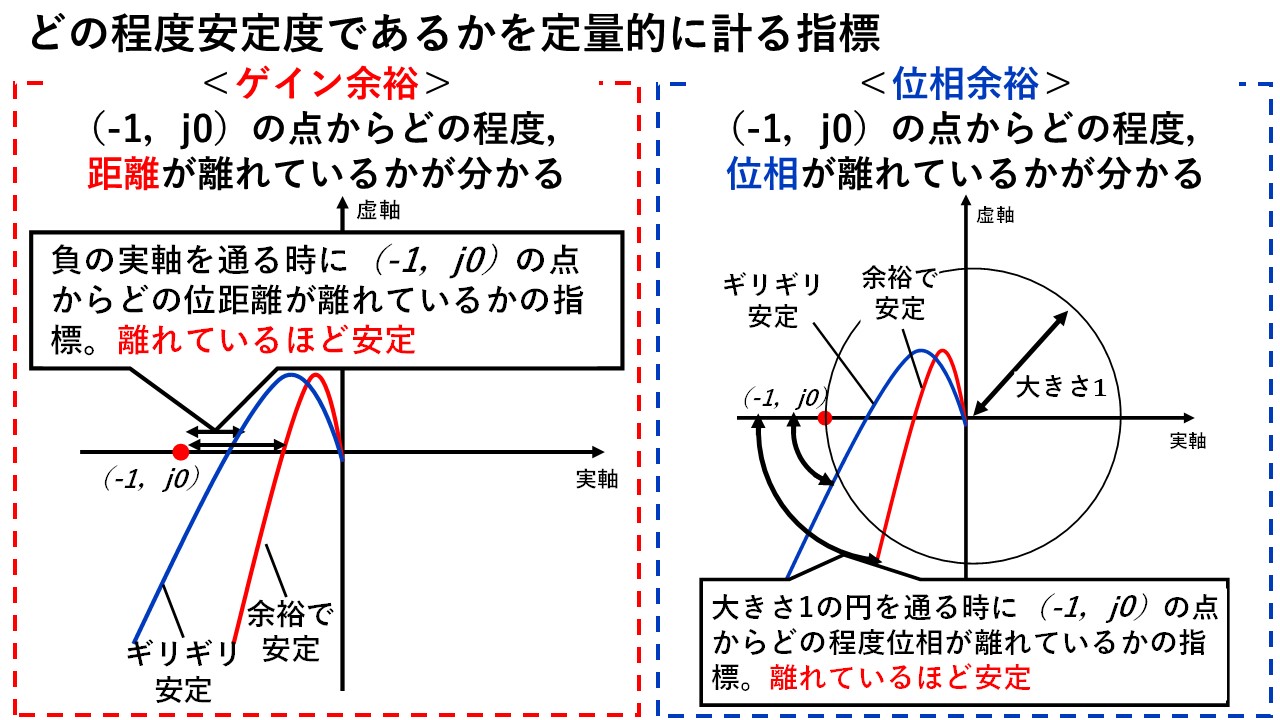
どの程度安定かを定量的に計る指標
どの程度安定かを把握する方法について説明しましたが，今のままだと(-1,j0)の点からどの程度離れているかが感覚的な判断になっていまいます！そこで必要になるのが，(-1,j0)の点からの距離を定量的に示す指標になります！それが，ゲイン余裕と位相余裕です(^^)/
ゲイン余裕とは，ωを0から∞に大きくしていったときの負の実軸を通る点と，（-1，j0）の点の距離を表します！当然距離が離れているほど，(-1,j0)の点を余裕を持って左側に見ることができますから，安定になります(^^)/
一方で，位相余裕とは，ωを0から∞に大きくしていったときの大きさ1になる点と，（-1，j0）の点の位相差を表します！当然位相差が大きいほど，(-1,j0)の点を余裕を持って左側に見ることができますから，安定になります(^^)/
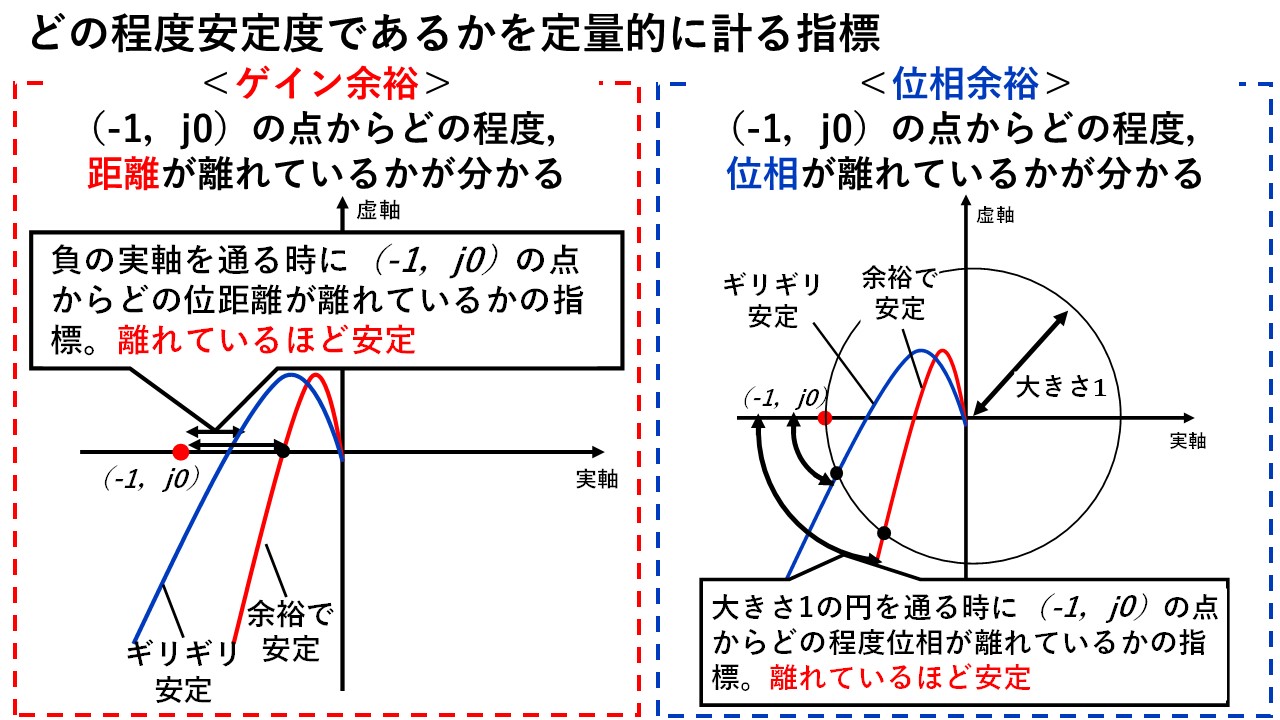図7 ゲイン余裕と位相余裕
ゲイン余裕と位相余裕はどちらも重要
ゲイン余裕と位相余裕を紹介しましたが，このうちどちらかが余裕であっても安心できません！例えば，以下の図8を見てみましょう！
左の図は，ゲイン余裕はあるが位相余裕がない場合の例です！ωを0から∞に大きくしていったときの負の実軸を通る点と（-1，j0）の点の距離はかなりあるのでゲイン余裕的には安定なのですが，位相余裕がないので(-1,j0)の点のすぐそばを通過していることが分かりますね！
一方で右の図は，位相余裕はあるがゲイン余裕がない場合の例です！ωを0から∞に大きくしていったときの大きさ1になる点と（-1，j0）の点の位相差は大きいので位相余裕はそれなりにあるのですが，ゲイン余裕がないので(-1,j0)の点のすぐそばを通過していることが分かりますね！
したがって，ゲイン余裕と位相余裕のどちらかが大きければ良いというわけではなく，システムの安定性の観点では，どちらもある程度確保する必要があるということですね(^^)/
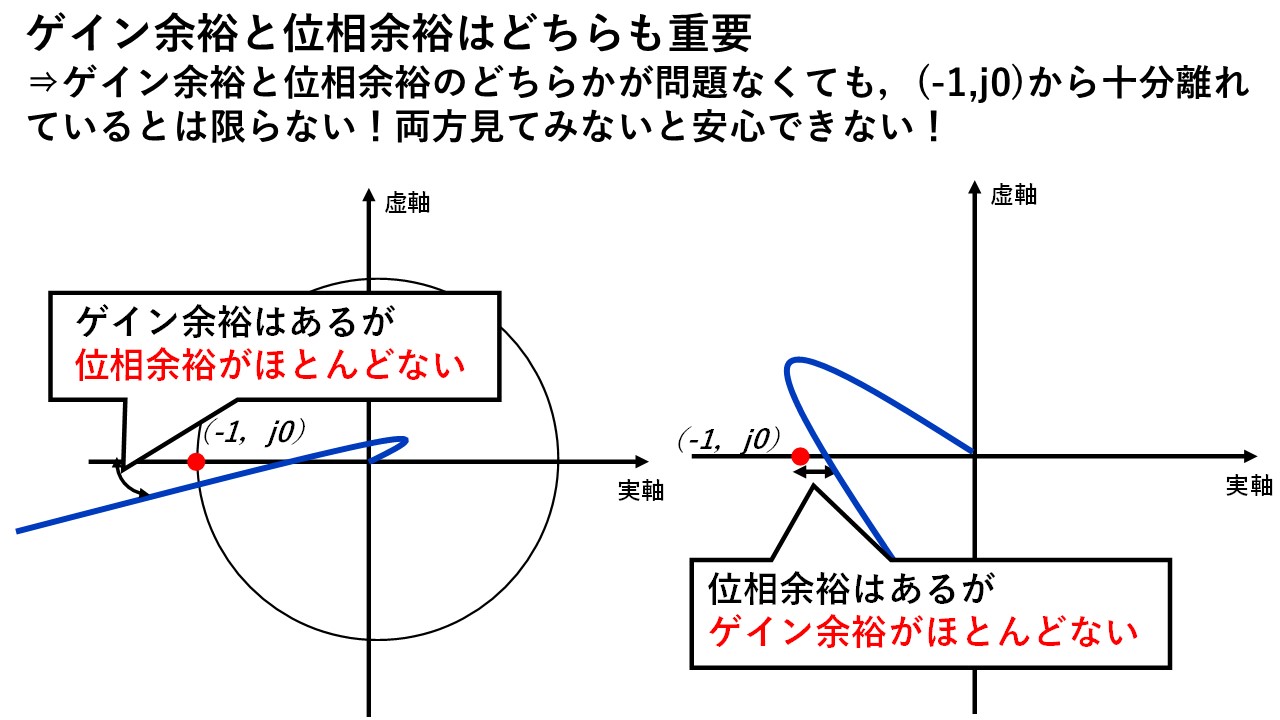図8 ゲイン余裕と位相余裕のどちらかしか確保されていない場合の例
今回の記事はここまでです！有難うございました(^^)/
